În caz de incertitudine
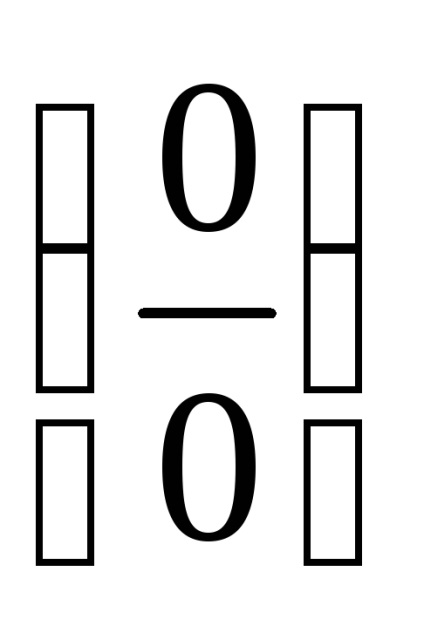
a) folosiți identitatea, unde
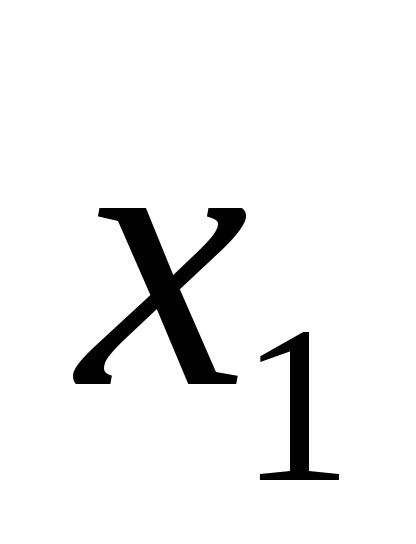
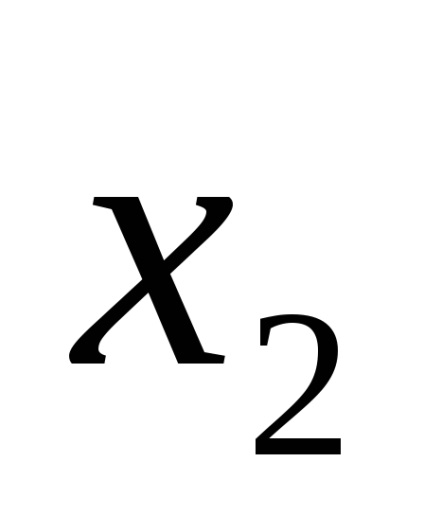
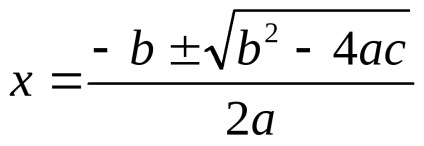
b) considera că atunci când
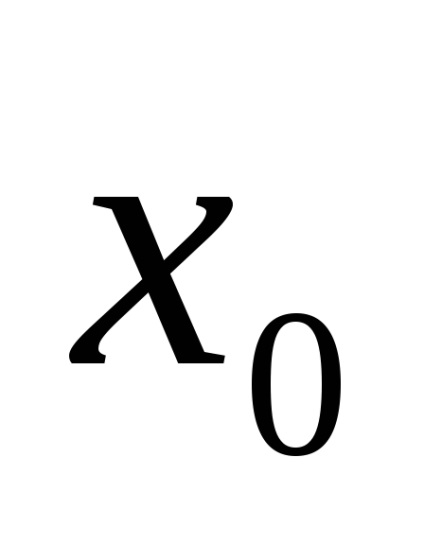
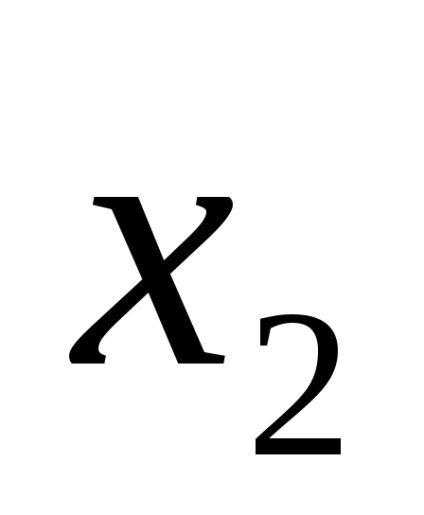
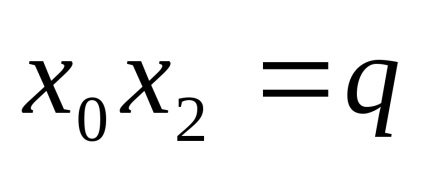
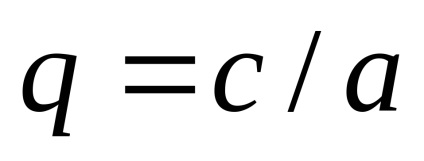
c) aplică egalitatea, unde
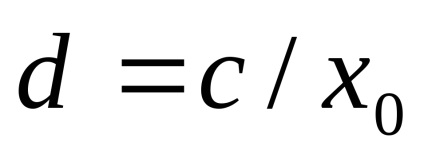
(ecuațiile au fost rezolvate și a fost utilizată prima metodă).
.
În ecuație, coeficientul liber -10 a fost împărțit de coeficientul din fața lui
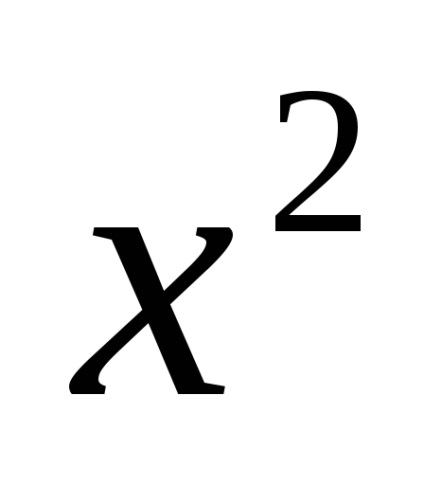
Apoi, a doua rădăcină a condiției
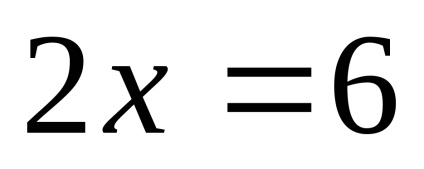
.
paranteză
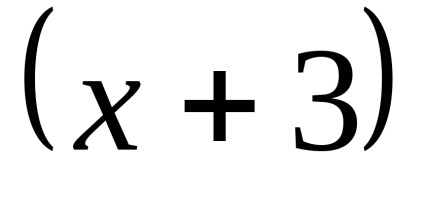
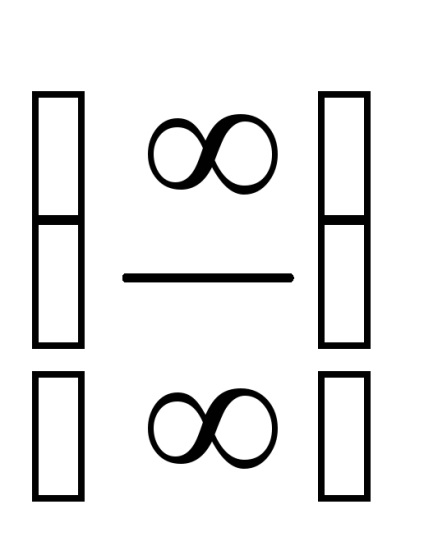
PR6. Descoperă incertitudinea
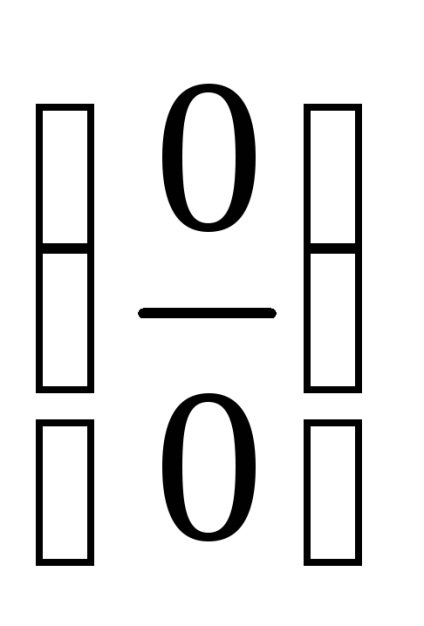
.
Limita unei funcții fracționale-raționale la infinit
Să i se dea o funcție
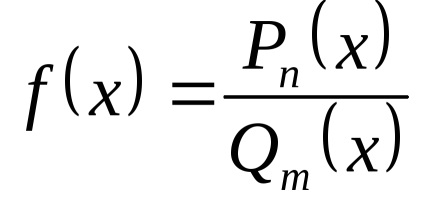
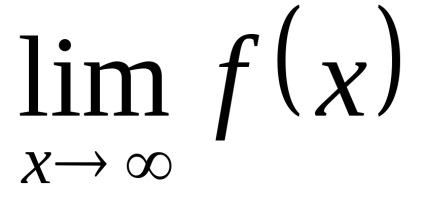
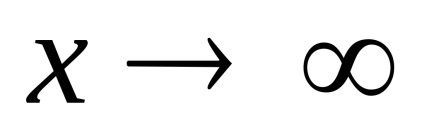
întreaga fracțiune se comportă ca raportul dintre gradele mai vechi:
.
Apoi. Semnificăm prin
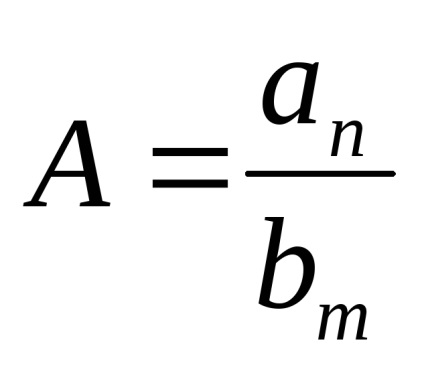
Astfel, limita este
a) infinit, dacă gradul numărătorului este mai mare decât gradul numitorului;
b) 0 în caz contrar;
c) împotriva coeficienților de conducere, dacă gradele sunt egale.
PR7. Găsiți limitele
PR8. Găsiți limitele
Exemplul 11. Lăsând puterile mai mari în numerotator și în numitor, găsim
Exemplul 12. Lăsând puterile mai mari, vedem asta
Rețineți că semnul infinit (dacă există) nu este indicat în răspuns. Cu toate acestea, dacă ambele grade superioare sunt chiar (sau ambii sunt ciudate), relația lor este întotdeauna pozitivă, care poate fi luată în considerare.
PR9. Găsiți limitele funcțiilor
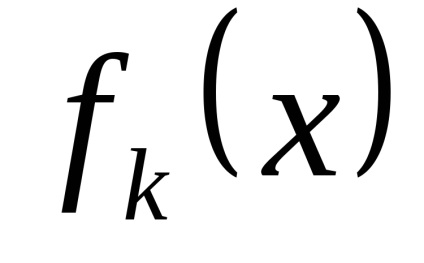
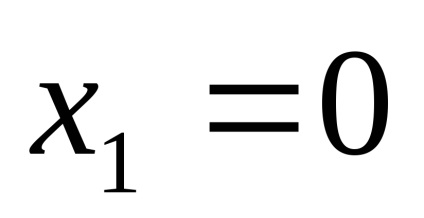
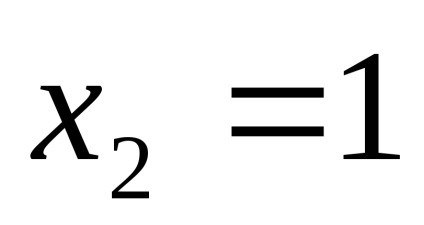
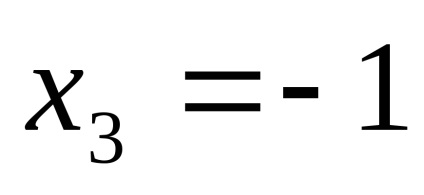
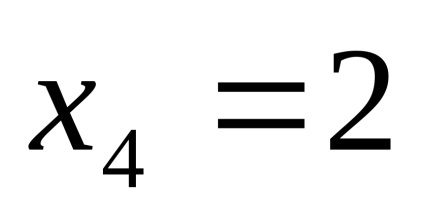
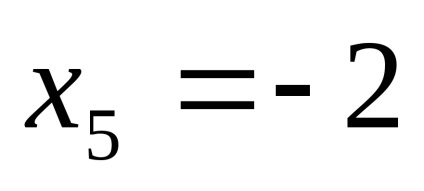
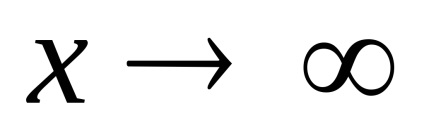
.
Limitele funcțiilor iraționale
Dacă funcția conține o rădăcină, înlocuiți, ca de obicei, punctul limită. Complexitatea este asociată cu incertitudinea
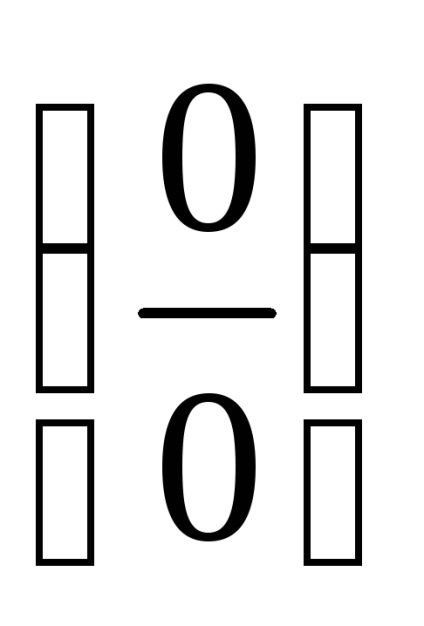
Expresiile sopryazhenyotnositelno diferențe la pătrat. dacă produsul lor se transformă într-o diferență de pătrate conform formulei.
Exemple de expresii conjugate
a)
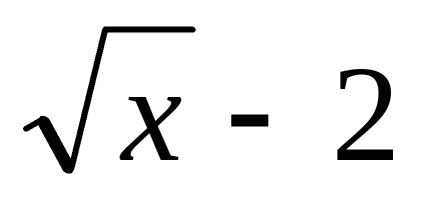
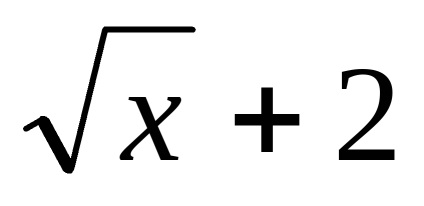
b)
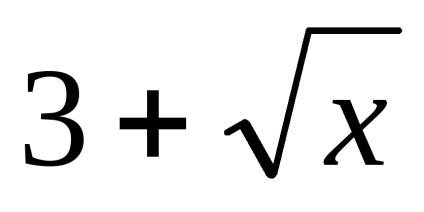
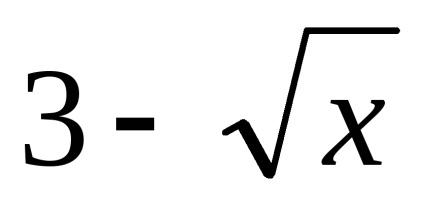
c)
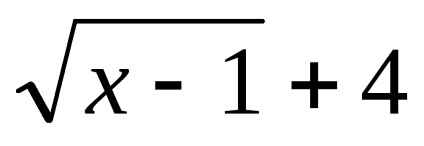
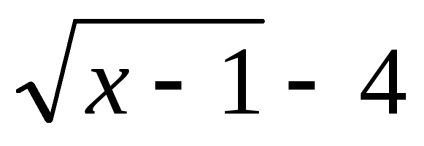
,
iar sub rădăcină totul rămâne neschimbat;
.
PR10. Găsiți limitele funcțiilor iraționale printr-o simplă substituire:
Exemplul 13. Înlocuind aceste puncte, găsim valorile
PR11. Descoperă incertitudinea
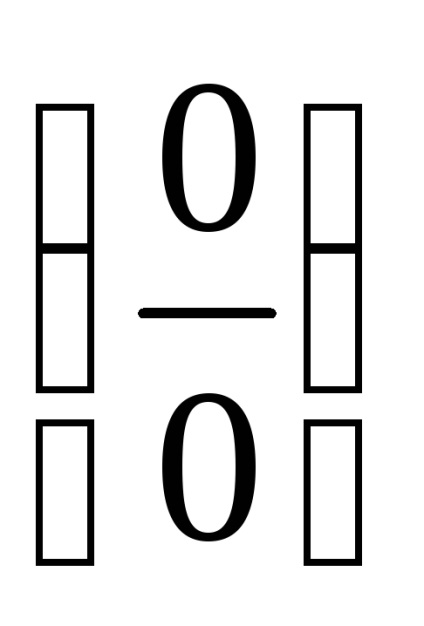
.
.
.
PR12. Înmulțiți numerotatorul și numitorul cu expresia conjugat la numărător și apoi la expresia conjugată cu numitorul. Prin reducerea parantezelor, extindeți incertitudinea
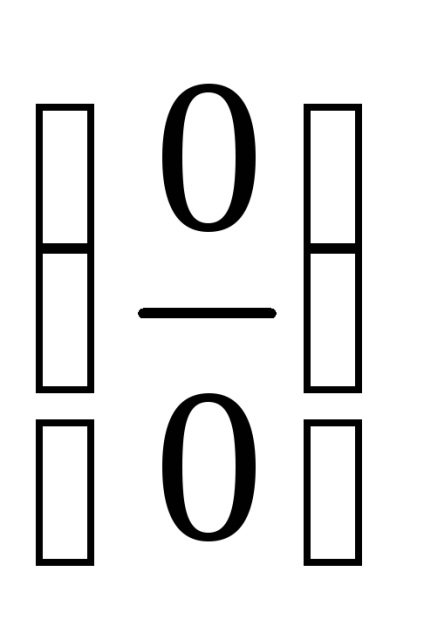
Exemplul 17. Înmulțiți pentru a obține diferența dintre pătrate:
.
Exemplul 18 în același mod ca în exemplul 17,
.
Limitele iraționale la
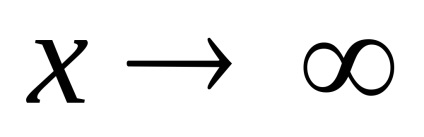
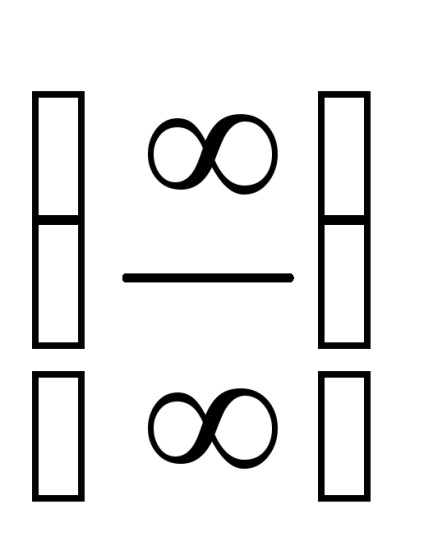
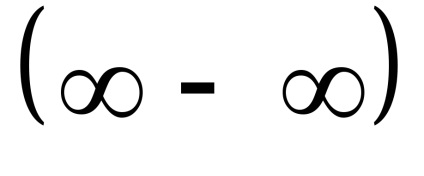
Articole similare
Trimiteți-le prietenilor: