În mod similar, multiplicarea ecuației (3.49) și integrarea în intervalul de la, obținem:
,
Astfel, coeficienții din seria (3.49) sunt determinați în mod unic prin formulele (3.50) - (3.52), care demonstrează teorema.
Această teoremă oferă motive pentru introducerea următoarei definiții.
Definiția. Serii funcționale:
unde coeficienții sunt determinați prin formule:
se numește seria Fourier a funcției f (x). Observăm asta mereu.
Să descoperim ce proprietăți trebuie să posede funcția f (x) pentru seria Fourier construită pentru a converge, astfel încât suma seriei Fourier construite să fie egală cu valorile funcției date la punctele corespunzătoare.
Definiția. Funcția f (x) se spune că este monotonică în bucăți pe intervalul [a. b] dacă segmentul poate fi împărțit cu un număr finit de puncte în intervale, astfel încât în fiecare dintre ele funcția este monotonă.
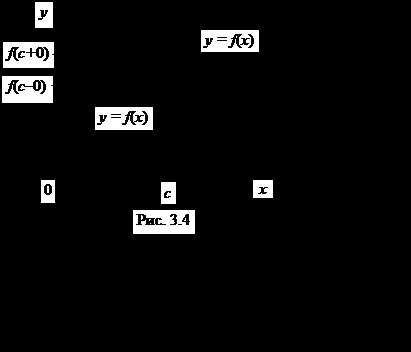
Rezultă din definiția că dacă funcția f (x) este monotonă și limitată în parte pe intervalul [a. b], atunci poate avea doar puncte de discontinuitate de primul tip. Într-adevăr, dacă există un punct de discontinuitate a funcției f (x), atunci, datorită monotonicității funcției, există limite:
și anume punctul este un punct de discontinuitate a primului tip (Figura 3.4).
TEOREM 3.7. Dacă funcția f (x) este periodică cu perioadă, parțial monotonică și limitată pe un interval, atunci
pentru orice punct de continuitate (adică, este suma seriei Fourier). Dacă punctul este un punct de discontinuitate a primului tip de funcție, atunci suma seriei Fourier în acest punct
,
unde sunt limitele la stânga și respectiv la dreapta, respectiv la punctul x.
Din teorema rezultă că în punctele de continuitate a funcției și suma este egală cu media aritmetică a limitelor la stânga și la dreapta funcției în punctele de discontinuitate a primului tip.
De asemenea, rezultă din teorema că clasa funcțiilor reprezentabile de seria Fourier este destul de largă. Prin urmare, seriile Fourier au găsit o aplicare largă în diferite ramuri ale matematicii. Seria Fourier este utilizată cu succes în fizica matematică și aplicațiile sale la probleme specifice ale mecanicii și fizicii.
Exemplul 1. Extindeți într-o serie Fourier o funcție având o perioadă și dată într-un interval după cum urmează:
Articole similare
-
Dreptul de vot și condițiile exercitării drepturilor electorale ale cetățenilor
-
Grădină și mobilier forjat - frumos, funcțional, de calitate - în vrac de la producător
Trimiteți-le prietenilor: