Unele proprietăți ale factorilor determinanți

Aici vom descrie acele proprietăți care sunt folosite de obicei pentru a calcula determinanții în cursul standard al matematicii superioare. Acesta este un subiect auxiliar, despre care vom face referire la secțiunile rămase după cum este necesar.







Deci, permiteți o matrice pătrată $ A _ = \ left (\ begin a_ a_ \ ldots a_ \ a__ a_ \ ldots a_ \\ ldots \ ldots \ ldots \ ldots \\ a_ a_ \ ldots a_ \\ \ end \ right) $. Fiecare matrice pătrată are o caracteristică numită determinant (sau determinant). Nu voi intra în esența acestui concept. Dacă este nevoie de o explicație, vă rugăm să vă dezabonați la forum. și voi aborda această problemă în detaliu.

Determinantul matricei $ A $ este notat ca $ \ Delta A $, $ | A | $ sau $ \ det A $. Ordinea determinantului este egală cu numărul de rânduri (coloane) din acesta.

  1. Valoarea determinantului nu se modifică dacă rândurile sale sunt înlocuite cu coloanele corespunzătoare; $ \ Delta A = \ Delta A ^ T $.

Exemplu de aplicare a acestei proprietăți: afișare / ascundere

Luați în considerare determinantul $ \ left | \ începe 2 5 \\ 9 4 \ end \ right | $. Vom găsi valoarea sa folosind formula # 1 din subiectul de calcul al factorilor determinanți ai ordinelor a doua și a treia.

$$ \ left \ începe 2 5 \\ 9 4 \ end \ right | = 2 \ cdot 4-5 \ cdot 9 = -37

Înlocuim rândurile cu coloane după principiul: "prima linie a fost prima coloană", "a doua linie a fost a doua coloană":

Unele proprietăți ale factorilor determinanți

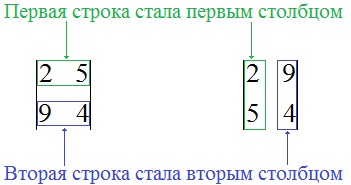
Calculăm determinantul determinant: $ \ left | \ începe 2 9 \\ 5 4 \ end \ right | = 2 \ cdot 4-9 \ cdot 5 = -37 $. După cum puteți vedea, valoarea determinantului de la înlocuitor nu a fost modificată.

  • Dacă schimbați două rânduri (coloane) ale determinantului, atunci semnul factorului determinant se modifică la contrariul.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Luați în considerare determinantul $ \ left | \ începe 2 5 \\ 9 4 \ end \ right | $. Să găsim valoarea sa, utilizând formula 1 din subiectul de calcul al determinanților ordinelor a doua și a treia.

    $$ \ left \ începe 2 5 \\ 9 4 \ end \ right | = 2 \ cdot 4-5 \ cdot 9 = -37

    Acum schimbăm prima și a doua rânduri. Obținem determinantul $ \ left | \ începe 9 4 \\ 2 5 \ end \ right | $. Calculăm determinantul determinant: $ \ left | \ începe 9 4 \\ 2 5 \ end \ right | = 9 \ cdot 5-4 \ cdot 2 = 37 $. Astfel, valoarea inițială a determinantul egal cu (-37), în timp ce determinant cu ordinea schimbată de rânduri este egal cu $ - (- 37) = $ 37. Semnul determinantului sa schimbat la contrariul.

  • Determinantul, pentru care toate elementele unui rând (coloană) sunt zero, este zero.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Deoarece în determinantul $ \ a plecat | \ începe -7 10 0 \\ -9 21 0 \\ 2 -3 0 \ end \ right | $ toate elementele celei de-a treia coloane sunt zero, atunci determinantul este zero, adică $ \ left | \ începe -7 10 0 \\ -9 21 0 \\ 2 -3 0 \ end \ right | = 0 $.

  • Un determinant ale cărui elemente dintr-un rând (coloană) sunt egale cu elementele corespunzătoare unui alt rând (coloană) este zero.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Deoarece în determinantul $ \ a plecat | \ începe -7 10 0 \\ -7 10 0 \\ 2 -3 18 \ end \ right | $ toate elementele primei linii sunt egale cu elementele corespunzătoare ale celui de al doilea rând, atunci determinantul este zero, adică $ \ left | \ începe -7 10 0 \\ -7 10 0 \\ 2 -3 18 \ end \ right | = 0 $.

  • Dacă în determinant toate elementele unui rând (coloană) sunt proporționale cu elementele corespunzătoare ale unui alt rând (coloană), atunci acest determinant este zero.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Deoarece în determinantul $ \ a plecat | \ începe -7 10 28 \\ 5 -3 0 \\ -15 9 0 \ end \ right | $ al doilea și al treilea rând sunt proporționale, adică $ III = -3 \ cdot II $, atunci determinantul este zero, adică $ \ left | \ începe -7 10 28 \\ 5 -3 0 \\ -15 9 0 \ end \ right | = 0 $.

  • Dacă toate elementele unui rând (coloană) au un factor comun, atunci acest factor poate fi luat în afara semnului determinantului.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Luați în considerare determinantul $ \ left | \ începe -7 10 \\ -9 21 \ end \ right | $. Rețineți că toate elementele celei de-a doua linii sunt împărțite în 3:

    $$ \ left \ începe -7 10 \\ -9 21 \ end \ right | = \ left \ începe -7 10 \\ 3 \ cdot (-3) 3 \ cdot 7 \ end \ right | $$

    Numărul 3 este factorul comun al tuturor elementelor din al doilea rând. Luăm cele trei pentru semnul determinantului:

    $$ \ left \ începe -7 10 \\ -9 21 \ end \ right | = \ left \ începe -7 10 \\ 3 \ cdot (-3) 3 \ cdot 7 \ end \ right | = 3 \ cdot \ left | \ începe -7 10 \\ -3 7 \ end \ right | $$

  • Determinantul nu se schimbă dacă toate elementele unui anumit rând (coloană) pentru a adăuga elementele respective alt rând (coloană), înmulțit cu un număr arbitrar.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Luați în considerare determinantul $ \ left | \ începe -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | $. Adăugați la elementele celei de-a doua linii elementele corespunzătoare ale celui de-al treilea rând, înmulțit cu 5. Scrieți după cum urmează:

    $$ \ left \ începe -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | \ începe \ phantom \\ II + 5 \ cdot III \\ \ phantom \ end $$

    A doua linie va fi schimbată, restul liniilor rămân neschimbate.

    $$ \ left \ începe -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | \ începe \ phantom \\ II + 5 \ cdot III \\ \ phantom \ end = \ left \ începe -7 10 0 \\ -9 + 5 \ cdotul 2 21 + 5 \ cdot (-3) 4 + 5 \ cdot 1 \\ 2 -3 1 \ end \ right | = \ left \ începe -7 10 0 \\ 1 6 9 \\ 2 -3 1 \ end \ right |. $$

  • Dacă în determinant un anumit rând (coloană) este o combinație liniară a altor rânduri (coloane), atunci determinantul este zero.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Imediat voi explica ce înseamnă expresia "combinație liniară". Să presupunem că avem rânduri (sau coloane): $ A_1 $, $ A_2 $. $ A_s $. expresie

    $$ k_1 \ cdot A_1 + k_2 \ cdot A_2 + \ ldots + k_s \ cdot A_S, $$

    unde $ k_i \ în R $ este numită o combinație liniară de rânduri (coloane) $ A_1 $, $ A_2 $. $ A_s $.

    De exemplu, luați în considerare un astfel de determinant:

    $$ \ left \ începe -1 2 3 0 \\ -2 -4 -5 1 \\ 5 0 7 10 \\ -13 -8 -16 -7 \ end \ right | $$

    În acest determinant, a patra linie poate fi exprimată ca o combinație liniară a primelor trei linii:

    $$ IV = 2 \ cdot I + 3 \ cdot II-III $$

    În consecință, factorul determinant este egal cu zero.

  • Dacă fiecare element al unora rând k (coloana k) a determinantului este egală cu suma a doi termeni, astfel determinant este egal cu suma determinanților în primul dintre care o (coloana k) k rând sunt primii termeni, iar al doilea factor determinant în rândul k (coloana k) sunt termeni dispuse doua. Alte elemente ale acestor determinanți sunt aceleași.

    Exemplu de aplicare a acestei proprietăți: afișare / ascundere

    Luați în considerare determinantul $ \ left | \ începe -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | $. Se scriu elementele celei de-a doua coloane după cum urmează: $ \ left | \ începe -7 3 + 7 0 \\ -9 21 + 0 4 \\ 2 5 + (-8) 1 \ end \ right | $. Apoi, acest determinant este egal cu suma a doi determinanți:

    $$ \ left \ începe -7 10 0 \\ -9 21 4 \\ 2 -3 1 \ end \ right | = \ left \ începe -7 3 + 7 0 \\ -9 21 + 0 4 \\ 2 5 + (-8) 1 \ end \ right | = \ left \ începe -7 3 0 \\ -9 21 4 \\ 2 5 1 \ end \ right | + \ left \ începe -7 7 0 \\ -9 0 4 \\ 2 -8 1 \ end \ right | $$

  • Factorul determinant al produsului a două matrice pătrată din aceeași ordine este egal cu produsul determinanților acestor matrice, adică $ \ det (A \ cdot B) = \ deț A \ cdot \ det B $. O generalizare a acestei reguli: $ \ det \ left (A ^ n \ right) = \ left (\ det A \ right) ^ n $.
  • Dacă matricea $ A $ - degenerate (adică determinant său nu este zero), atunci $ \ det \ stânga (A ^ \ dreapta) = \ frac $.






    • Formule pentru calcularea factorilor determinanți

    Pentru determinanții ordinelor a doua și a treia, sunt valabile următoarele formule:

    Determinantul matricei $ A_ $ poate fi extins în rândul i, folosind următoarea formulă:

    Un analog al acestei formule există pentru coloane. Formula pentru expansiunea determinantului pe coloana jth este urmatoarea:

    Ne indică o altă formulă de calcul determinanți matrici triunghiulare triunghiulare superioare și inferioare (a se vedea explicarea acestor termeni. Tema „Matrix. Tipuri de matrici. Termenii de bază“). Determinantul unei astfel de matrice este egală cu produsul elementelor de pe diagonala principală. exemple:

    \ începe \ left | \ începe 2 -2 9 1 \\ 0 9 8 0 \\ 0 0 4 -7 \\ 0 0 0 -6 \ end \ right | = 2 \ cdot 9 \ cdot 4 \ cdot (-6) = - 432. \\ \ left | \ începe -3 0 0 0 \\ -5 0 0 0 \\ 8 2 1 0 \\ 5 4 0 10 \ end \ right | = -3 \ cdot 0 \ cdot 1 \ cdot 10 = 0. \ end







    Articole similare

    Pagina anterioară

    Pagina următoare

    Trimiteți-le prietenilor: