La rezolvarea problemelor științifice și tehnice, este adesea necesar să se descrie matematic orice sistem dinamic. Cel mai bine este să faceți acest lucru sub forma unor ecuații diferențiale (DU) sau a unui sistem de ecuații diferențiale. Cel mai adesea ele sunt o astfel de problemă apare în rezolvarea problemelor asociate cu modelarea cinetica reacțiilor chimice și a diferitelor fenomene de transport (căldură, masa, impuls) - transfer de căldură, de amestecare, uscare, adsorbție, în care descrie mișcarea de macro și micro-particule.
Într-o serie de cazuri, ecuația diferențială poate fi transformată într-o formă în care cel mai mare derivat este exprimat într-o formă explicită. O astfel de formă de scriere se numește o ecuație rezolvată în raport cu cel mai mare derivat (în acest caz, nu există derivat superior în partea dreaptă a ecuației):
O soluție a unei ecuații diferențiale obișnuite este o funcție y (x), care pentru orice x satisface această ecuație într-un interval definit finit sau infinit. Procesul de rezolvare a unei ecuații diferențiale se numește integrarea unei ecuații diferențiale.
Din punct de vedere istoric, prima și cea mai simplă metodă pentru rezolvarea numerică a problemei Cauchy pentru primul ME este metoda lui Euler. Se bazează pe aproximarea prin derivat a raportului dintre incrementările finale ale variabilelor dependente (y) și independente (x) dintre nodurile grilajului uniform:
unde yi + 1 este valoarea dorită a funcției la punctul xi + 1.
Acuratețea metodei Euler poate fi îmbunătățită dacă vom folosi formula de integrare mai precisă - formula trapezoidală pentru a aproxima integralele.
Această formulă este implicită în ceea ce privește yi + 1 (această valoare este atât în partea stângă, cât și în partea dreaptă a expresiei), adică este o ecuație pentru yi + 1. care poate fi rezolvată, de exemplu, numeric, folosind o metodă iterativă (în această formă poate fi considerată o formulă iterativă a metodei simple de iterație).
Cursul constă în trei părți. În prima parte o scurtă descriere a metodelor. În a doua parte, formularea și soluționarea problemei. În a treia parte - implementarea software-ului în limbajul calculatorului
Scopul lucrării: să studiem două metode de rezolvare a ecuațiilor diferențiale - metoda Euler-Cauchy și metoda îmbunătățită Euler.
1. Partea teoretică
Ecuațiile diferențiale obișnuite (ODE)
Ecuații diferențiale în derivatele parțiale.
Ecuațiile diferențiale obișnuite sunt acele ecuații care conțin unul sau mai mulți derivați ai funcției dorite. Ele pot fi scrise ca
Cea mai mare ordine care intră în ecuația (1) este numită ordinea ecuației diferențiale.
Cea mai simplă (liniară) ODE este ecuația (1) a ordinului permis în raport cu derivatul
O soluție a ecuației diferențiale (1) este orice funcție care, după ce o substituie într-o ecuație, o transformă într-o identitate.
Principala problemă asociată cu o ODE liniară este cunoscută sub numele de problema Kashi:
Găsiți soluția de (2) sub forma unei funcții care satisface condiția inițială (3)
Din punct de vedere geometric, aceasta înseamnă că este necesară găsirea curbei integrale care trece prin punctul) atunci când egalitatea (2) este satisfăcută.
Numeric din punctul de vedere al problemei Kashi înseamnă: este necesar să se construiască un tabel cu valori ale ecuației (2) satisfăcătoare a funcției și condiția inițială (3) pe un segment cu o anumită etapă. Se presupune, de obicei, că condiția inițială este dată la capătul din stânga al segmentului.
Cea mai simplă metodă numerică pentru rezolvarea unei ecuații diferențiale este metoda Euler. Se bazează pe ideea construirii grafice a soluției unei ecuații diferențiale, dar această metodă oferă, de asemenea, o modalitate de a găsi funcția dorită în formă numerică sau într-o tabelă.
Fie ca ecuația (2) să fie dată cu condiția inițială de a pune problema Kashi. Mai întâi rezolvăm următoarea problemă. Găsiți valoarea aproximativă a soluției la un anumit punct în cel mai simplu mod în care este un pas suficient de mic. Ecuația (2) împreună cu condiția inițială (3) specifică direcția tangentă a curbei integrate dorite în punctul cu coordonatele
Ecuația tangentei are forma
Deplasând de-a lungul acestei tangente, obținem valoarea aproximativă a soluției la punctul:
Având o soluție aproximativă într-un punct, este posibilă repetarea procedurii descrise anterior: se construiește o linie dreaptă care trece prin acest punct cu un coeficient unghiular și de-a lungul ei se găsește valoarea aproximativă a soluției în punctul
. Rețineți că această linie nu este tangentă la curba integrală reală, deoarece punctul nu este disponibil pentru noi, dar dacă este suficient de mic, atunci cele aproximative obținute vor fi aproape de valorile exacte ale soluției.
Continuând această idee, construim un sistem de puncte echidistant
Obținerea tabelului valorilor funcției necesare
prin metoda lui Euler constă în aplicarea ciclică a formulei
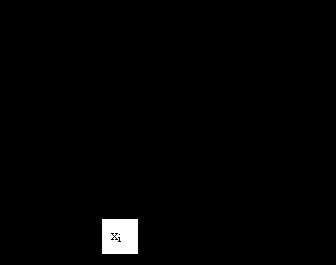
Figura 1. Interpretarea grafică a metodei Euler
Metodele de integrare numerică a ecuațiilor diferențiale, în care soluțiile sunt obținute de la un nod la altul, se numesc cele incrementale. Metoda lui Euler este cel mai simplu reprezentant al metodelor pas cu pas. Particularitatea oricărei metode pas cu pas este aceea că pornind de la a doua etapă, valoarea inițială din formula (5) este ea însăși aproximativă, adică eroarea la fiecare etapă următoare crește în mod sistematic. Metoda cea mai răspândită pentru estimarea preciziei metodelor pas cu pas a unei soluții numerice aproximative a ODE este metoda de traversare dublă a unui segment dat cu etapa și cu etapa
1.1 Metoda Euler îmbunătățită
Ideea de bază a acestei metode: calculat prin formula (5), valoarea următoare va fi mai exactă dacă valoarea derivată, adică panta unei substituției curbe integrant direct pe segmentul nu va fi calculată de la marginea din stânga (adică punctul), iar segmentul de mijloc. Dar, ca valoarea derivatului dintre punctele nu se calculează, apoi se trece la zonele gemene ale centrului, care este punctul cu ecuația liniară devine forma:
Și formula (5) ia forma
Formula (7) este aplicată numai pentru că nu pot fi obținute valori pe ea, prin urmare, ele se găsesc prin metoda Euler, pentru a obține un rezultat mai precis, procedați după cum urmează: de la început, conform formulei (5)
La punctul a, atunci se găsește prin formula (7) în trepte
După ce se calculează alte calcule utilizând formula (7)
1.2 Metoda Euler-Cauchy
Din punct de vedere geometric, aceasta înseamnă că direcția curbei integrale la punctul de pornire și la punctul auxiliar este determinată de la început, iar valoarea medie a acestor direcții este luată ca direcție finală.
2. Declarația și soluționarea problemei
Rezolvați ecuația diferențială prin metoda îmbunătățită Euler și metoda Euler-Cauchy utilizând exemplul ecuației nu
2.1 Soluția problemei prin metoda îmbunătățită a lui Euler
Rezolvați ecuația diferențială prin metoda îmbunătățită Euler utilizând exemplul unei ecuații de nu cu acuratețe
facem un pas. găsim:
Să luăm, ca exemplu, ecuația lui ny cu precizie.
Rezultatul programului este prezentat în Figura 2 a), b):
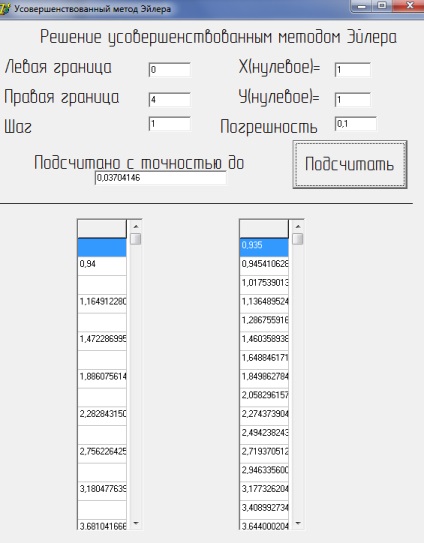
Figura 2 a) Implementarea pe computer a unui test de caz îmbunătățit
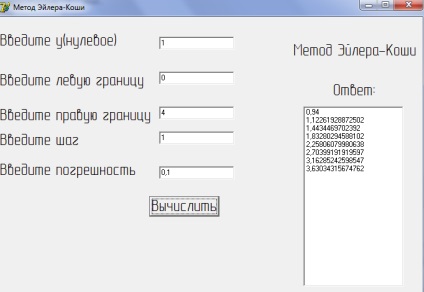
Figura 2 b) Implementarea unui exemplu de testare a metodei Euler-Cauchy pe un computer
Deci, după cum se știe în prealabil, soluția ecuației și coincide cu rezultatul obținut în program, se poate concluziona că programul funcționează corect.
Dacă introduceți a> b, programul va face următoarele:
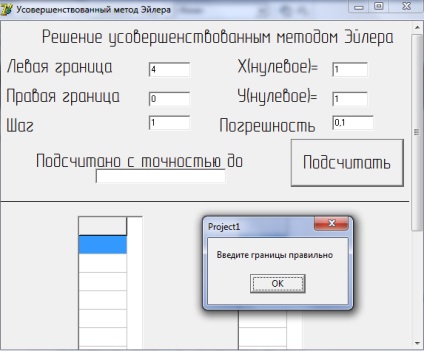
Figura 3 - Rezultatul rezolvării ecuației prin metoda îmbunătățită Euler la introducerea a> b
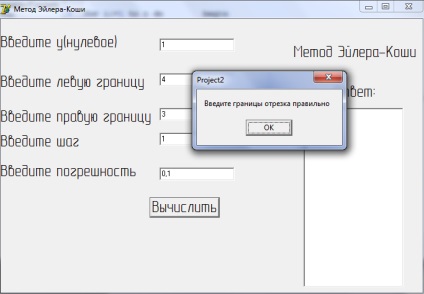
Figura 4 - Rezultatul soluției ecuației prin metoda Euler-Cauchy cu introducerea a> b
Dacă eroarea nu este corect introdusă, programul va continua după cum urmează:
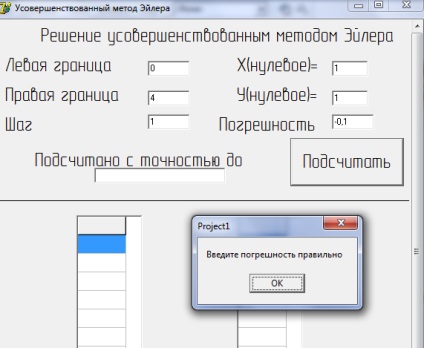
Figura 5 - Rezultatul rezolvării ecuației prin metoda îmbunătățită Euler cu eroare introdusă incorect
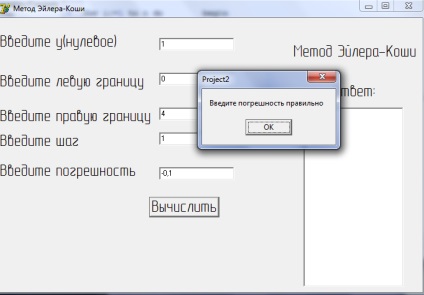
Figura 6 - Rezultatul soluției ecuației prin metoda Euler-Cauchy cu eroare introdusă incorect
3.4. Soluția problemei cu ajutorul unui computer
Să luăm, ca exemplu, ecuația lui ny cu precizie.
Când rezolvăm o ecuație dată în limba de programare Borland Delphi, obținem următoarele rezultate (Figura 3):
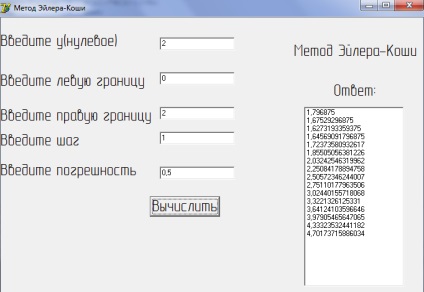
Figura 7 Implementarea lui Euler-Cauchy
Să luăm, ca exemplu, ecuația lui ny cu precizie.
Când rezolvăm o ecuație dată în limba de programare Borland Delphi, obținem următoarele rezultate (Figura 4):
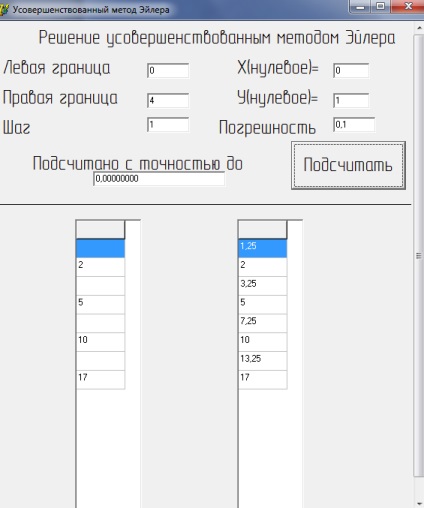
Figura 8Introducerea metodei avansate a lui Euler
Tabelele 1 și 2 prezintă rezultatul activității programelor atunci când se specifică diferite date inițiale.
Tabelul 1 - Rezultatele programului pentru o metodă îmbunătățită Euler
concluzie
Astfel, este evident că în calculul ecuației diferențiale prin metodele Euler-Cauchy și prin metoda îmbunătățită Euler, soluția nu ne dă o valoare exactă, ci doar o aproximație.
Cu cât este mai mic intervalul de calcul și etapa de operare, cu atât mai exact rezultatul obținut de mașină. Pentru o mai mare acuratețe, este necesar un număr mai mare de iterații, ceea ce determină o creștere a timpului petrecut în calculul integral al calculatorului invers proporțional cu precizia calculului.
Utilizarea a două metode de calcul simultan ne-a permis să investigăm dependența corectitudinii calculelor în aplicarea ambelor metode. Pe care se poate trage o concluzie clară că metoda îmbunătățită Euler este mai ușor pentru mașină și rezultatul (care este foarte apropiat de cel existent) este mai rapid decât metoda Euler-Cauchy. Dar metoda Euler-Cauchy este mai exactă.
Programele sunt scrise în limba Borland Delphi pentru rezolvarea ecuațiilor diferențiale. Soluțiile obținute ca urmare a lucrărilor programelor coincid cu răspunsurile din exemplu
Lista literaturii utilizate
Samarskii AA, A. Gulin, A. V. Metode numerice: Proc. manual pentru universități. - M. Science. Ch. Ed. Fizică și Matematică. Literatura. 1989. - 432 p.
Arta similara:
Metode iterative pentru rezolvarea ecuațiilor neliniare
). Clasificarea metodelor de soluție și a metodelor numerice pentru integrarea ecuațiilor diferențiale. Conceptele problemei Cauchy și etapa de integrare. Metoda aproximărilor succesive (metoda Piccard). Metoda lui Euler.
Euler. Euler a continuat să dezvolte teoria ecuațiilor diferențiale. începută în lucrările lui Leibniz și Bernoulli. Teoria ecuațiilor diferențiale. O. Cauchy a creat. Morse a creat un telegraf îmbunătățit, c. metoda de "încercare și eroare" ca mijloc de soluționare.
Metode de calculare a calculatoarelor și aplicarea acestora la probleme fizice
Un exemplu este o ecuație diferențială cu condițiile inițiale. Soluția generală a ecuației diferențiale este. 1 ... m este numărul de ecuații. k este numărul punctului calculat anterior. Metoda îmbunătățită Euler -Cash cu rafinament. Această metodă se bazează pe.
Cheat Sheet >> Calculatoare, Programare
Îmbunătățirea fiabilității execuției aplicațiilor, oferă componente avansate pe 32 de biți și, în acest caz. Să luăm în considerare câteva metode numerice pentru rezolvarea unei astfel de ecuații. 1.4. Metoda de iterații simple. Fie ecuația f (x) = 0, unde f (x) -.
Metode numerice. Practica de laborator
Articole similare
-
Rezolvarea ecuatiilor si a sistemelor de ecuatii in matematica
-
Eliminarea papilomului cu celandină este o metodă eficientă de rezolvare a problemei
Trimiteți-le prietenilor: