Tipuri de date și cum să lucrați cu ele
Sistemele de matematică informatică, ca orice alt software, lucrează cu datele și le procesează. Deoarece CSM axat pe pregătirea diverselor documente (inclusiv documente electronice și cărți), ele au un set extins de posibile tipuri și instrumente de date pentru a lucra cu ei. În acest capitol sunt discutate tipurile de date ale sistemelor Maple 9.5 / 10 și modul de lucru cu ele.
Alfabetul Maple-language (atât de intrare și programare) conține 26 caractere mici (a la z), 26 litere mari (A la Z), 10 cifre arabe (de la 0 la 9) și 32 de caractere speciale (aritmetică operatorii +, -, *, /, gradul de construcție semn ^, etc) .. În plus, există mai multe simboluri matematice speciale. Toate acestea vor fi descrise în acest capitol. Pentru a introduce caractere utilizând tastatura și simboluri matematice.
Există cinci perechi de simboluri alternative (adică același lucru):
Următoarele elemente ale sintaxei limbii sunt relevante pentru caracterele speciale simple și compuse:
•% - variabila de sistem care stochează rezultatul operațiunii anterioare;
•. - o blocare de expresie care împiedică ieșirea calculului să fie trimisă către celula de ieșire;
•; - o clemă de expresie care dă ieșirea rezultatului calculului către celula de ieșire;
• "- un delimiter de șir (de exemplu, șir");
•: = - Operatorul de atribuire (de exemplu, x: = 5);
•. - pointer de tip variabil (de exemplu, n :: integer sau z :: complex);
• \ - semnul diviziunii inverse, care are mai multe valori în funcție de context (vezi ajutor pentru acest semn - backslash).
Cuvintele rezervate sunt folosite pentru a crea expresii condiționate, bucle, proceduri și comenzi de control. Lista de cuvinte rezervate în sistemul Maple este prezentată mai jos.
și descrierea Break by Catch
do Done elif Închidere
eroare Exportați fi În sfârșit pentru
de la Global dacă se intersectează
modulul mod minus local următor
nu Opțiuni opțiune Od sau
proc Quit citește Return to save
opriți apoi să încercați uniunea
Aceste cuvinte nu pot fi numite obiecte utilizator.
Setul de reguli prin care se scriu definițiile tuturor obiectelor în limbajul Maple se numește sintaxa sa. Unele caracteristici ale sintaxei sunt utile pentru a cunoaște deja la începutul dezvoltării Maple. De exemplu, semnul - (minus) are un dublu sens. Aplicată la un singur număr, variabilă sau expresie, acesta își schimbă semnul. Cu toate acestea, două semne minus la rând (de exemplu, într-o înregistrare - 3) nu pot fi specificate. Un alt scop al semnului minus este de a crea o operație de scădere, de exemplu, 5-2 sau a-b. În consecință, atribuirea dublă are și semnul +, iar numărul nesemnificativ este considerat pozitiv, deci + 5 = 5.
Când introduceți numere reale pentru a indica comanda, utilizați simbolul ^ (de exemplu, 2 * 10 ^ 100 sau 2 * 10 ^ -100). Pentru a ridica un număr la putere, împreună cu operatorul ^, se poate utiliza și operatorul compus ** (doi asteriscuri la rând). Parenthesis este folosit pentru a schimba prioritatea general acceptată a calculelor, iar parametrii funcțiilor și procedurilor sunt de asemenea stabiliți în ele. Sintaxa limbii Maple este discutată mai detaliat mai jos.
Unii operatori sunt reprezentați de două simboluri - de exemplu, operatorul de atribuire a valorilor lor la variabile: = conține un colon și un semn egal. În astfel de afirmații, un caracter spațial nu este permis între caractere. Cu toate acestea, acesta poate fi folosit între diferite părți ale expresiei - deci, (a + b) / c este echivalent cu (a + b) / c.
Maple oferă o muncă destul de naturală cu întregi. În special, este posibil să se schimbe semnul unui număr și să se efectueze operații aritmetice de bază cu numere. Având în vedere cunoștințele bine cunoscute ale operațiunilor aritmetice, definiția lor nu este dată. Ne limităm la exemple de operațiuni simple cu numerele enumerate mai jos:
Rezultatele operațiilor cu întregi în cazul general sunt reprezentate de numere raționale. care sunt relații de numere întregi.
Punctul zecimal din numerele are un statut special - o indicație oriunde numere, inclusiv la sfârșitul anului, nu numărul de reale și conduce la traducerea de calcul în modul de lucru cu numere reale. De exemplu:
.3600000000 10 -13
Numărul de cifre după punct zecimal poate fi controlat prin setarea valorii variabilei de mediu a sistemului Cifre:
> Cifre: = 10; exp (1.);
Cifre: = 102,718281828
> Cifre: = 40: evalf (Pi);
După cum puteți vedea din aceste exemple, intrarea și ieșirea numerelor au următoarele caracteristici:
• pentru a separa întreaga parte a mantistei de cea fracționată, utilizați punctul de separare;
• mantisa zero nu este afișată (numărul începe cu un punct de separare);
• Mantisa este separată de ordine de un spațiu, care este tratat ca un semn de înmulțire;
• partea imaginară a numerelor complexe este dată prin înmulțirea cu simbolul unității imaginare I (rădăcina pătrată de -1);
• Dacă este posibil, Maple reprezintă un rezultat numeric sub forma unui număr exact rațional (raportul dintre două numere întregi).
Pentru a lucra cu numere, Maple are multe funcții. Acestea vor fi luate în considerare în viitor. Utilizând funcția multifuncțională Convert Maple poate converti numere cu diferite baze (de la 2 la 36, inclusiv binar și hexazecimal) în numere zecimale:
> convertire ("11001111", zecimal, binar);
> convertire ("1AF.C", zecimal, hex);
> convert ("Maple", zecimal, 36);
Datorită abilității de a efectua calcule simbolice, Maple, ca și alte SKA, implementează o aritmetică exactă. Aceasta înseamnă că rezultatul poate fi obținut cu orice număr de cifre exacte. Cu toate acestea, trebuie reținut faptul că se efectuează calcule numerice, în mod ideal, precise, numai în cazul operațiilor întregi, de exemplu, după cum se arată mai jos:
942594775983835942085162312448293674956231279470254376832 \ 788935341697759931622147650308786159180834691162349000 \ 3549599583369706302603264000000000000000000000000
Rețineți că, în ultimul exemplu, precizia este drastic pierdută, deoarece exponentul de 100.0 a fost specificat ca număr de punct floating. În consecință, rezultatul a fost sub forma unui astfel de număr. Numărul de cifre valide ale rezultatului este setat de variabila de sistem Cifre (implicit 10).
Iată câteva exemple de calcule precise ale unor funcții (cu o precizie de 150 de caractere din mantisă):
0,84147098480789650665250232163029899962256306079837106567 \ 275170999191040439123966894863974354305269585434903790 \ 7920674293259118920991898881193410327729
Maple si Mathematica sisteme dezvoltatorii susțin că, în principiu, posibile calcule și virgulă mobilă cu sarcina de a o mantisă milioane de numere exacte. Practic, această precizie nu este aproape niciodată necesară, cel puțin pentru fizicieni și ingineri. De exemplu, doar 39 de cifre exacte ale numărului π sunt suficiente pentru a calcula circumferința întregului univers în interiorul diametrului atomului de hidrogen. Cu toate acestea, adevărații matematicieni la un moment dat au fost pur și simplu "obsedați" cu calculul numărului π cu mare precizie. Cineva care și-a petrecut toată viața în asta. Ramanujan a avut o contribuție remarcabilă la astfel de calcule, care în 1916 a propus algoritmi și formule pentru calculul numărului π cu precizie arbitrară.
În Fig. 2.1 Este prezentată sarcina uneia dintre cele mai faimoase formule ale lui Ramanujan. Deja primul termen al sumei de formula (k = 1) dă o valoare de π cu un calcul de eroare cel puțin 3 # 8729; 10 -8. Creșterea lui k cu 1 de fiecare dată crește numărul de zecimale valide cu 8, adică o sută de milioane de ori! În principiu, această formulă poate renunța la un miliard sau mai multe semne exacte ale numărului π!
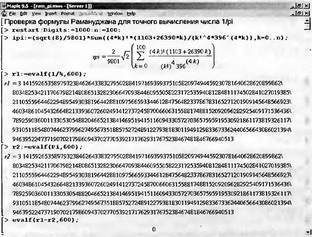
Fig. 2.1. Verificarea calculelor prin formula Ramanujan
Inginerii formulei Ramanujan pot provoca un atac de durere de cap sau durere de dinți. Este dureros de ciudat la prima vedere. Ce fel de precizie se poate spune dacă pe marea majoritate a limbajelor de programare se calculează rădăcina pătrată a doi, factoriali și gradați, cu doar 8-15 semne exacte?
Dar, sistemele Maple 9.5, datorită aparatului aritmetic de precizie încorporată, pot asigura o verificare eficientă a acestor formule. În cazul nostru, ne-am limitat la cazul în care n = 100 (valoarea maximă a k) și a avut loc un calcul „numai“ 600 de cifre ale π - cu faptul că rezultatele împreună într-o singură imagine. Și ei vorbesc de la sine - toate numerele din calcularea numărului tt și formula Ramanujan pe built-in algoritmul Maple a coincis, iar eroarea calculată este zero!
Maple, firește, ca și alte CSM, poate lucra cu numere complexe ale formulei z = Re (z) + I # 8729; Im (z). Unitatea imaginară din numărul complex (rădăcina pătrată de -1) este notată ca I. Funcțiile Re (z) și Im (z) returnează părțile reale și imaginare ale numerelor complexe. Pe planul complex, numerele sunt date de coordonatele punctelor (x, y) - Fig. 2.2.

Fig. 2.2. Reprezentarea numerelor obișnuite și complexe în plan
Pentru a reprezenta numerele din Fig. 2.2 se utilizează funcția pointplot (list), unde lista este o listă a coordonatelor punctelor. Această funcție devine disponibilă atunci când pachetul de parcele este conectat la comanda cu (parcele). În plus, este afișată funcția de afișare a unui număr de obiecte grafice într-un singur grafic (consultați descrierea reprezentării numerelor complexe de mai jos).
Exemple de specificare a unui număr complex și derivarea părților sale reale și imaginare sunt prezentate mai jos:
Numerele complexe sunt reprezentate de obicei pe așa-numitul plan complex, în punctele în care coordonatele x specifică partea reală a numărului complex, iar y (axa imaginară) arată partea imaginară a unui astfel de număr. În Fig. 2.2 prezintă sarcina sub formă de vectori de rază a numărului complex z = 4 + 3I, -z și numărul conjugat complex 4-3I. Și în Fig. 2.3 prezintă un exemplu de calcul al rădăcinilor ecuației z ^ n = 1 pentru cazul n = 16 (alte cazuri cititorul poate lua în considerare independent, pur și simplu schimbă n). Este ușor de observat că rădăcinile ecuației sunt numere complexe și că pe planul complex se află pe un cerc de rază a unității.

Fig. 2.3. Calcularea rădăcinilor ecuației z ^ n = 1 și localizarea rădăcinilor în planul complex
Raza cercului este valoarea absolută a unui număr complex z = a + b * I. Este un set geometric de numere complexe formate prin capătul rotativ al vectorului raza z în jurul începutul său la punctul (0, 0) în planul complex, așa cum este ilustrat printr-un exemplu și figură specifică . 2.2. Mai târziu, ne vom uita la o serie de funcții pentru lucrul cu numere complexe.
Numerele pot servi ca intrări, ieșiri și constante incluse în expresiile matematice. Tipul funcției (x, numeric) permite să se determine dacă x este un număr. Dacă este, ea returnează un adevărat boolean și, dacă nu, este fals (fals). De exemplu:
Articole similare
-
Capitolul 8 Freelancing sau lucrul în studio - de unde să începem
-
Diferența dintre tipurile de date celulare și formatul celular în Excel
Trimiteți-le prietenilor: