Avantajul acestor metode este acela că reduc soluția problemei valorii limită pentru o ecuație diferențială la soluția unui sistem de ecuații algebrice în raport cu valorile funcției dorite pe un anumit set de puncte. Acest lucru se realizează prin înlocuirea derivaților care intră în ecuația diferențială prin aproximările lor finite.
Considerăm esența unei astfel de metode de soluție pentru o ecuație diferențială de ordinul doi (1.41) pentru condițiile de graniță date (1.42). Împărțim segmentul [0,1] în n părți egale cu punctele xi = ih (i = 0,1, n). Reducem soluția problemei de limită-valoare (1.41), (1.42) la calculul valorilor funcției de rețea yi la punctele nodului xi. Pentru a face acest lucru, vom scrie ecuația (1.42) pentru nodurile interne:
Înlocuim derivații care intră în aceste relații prin aproximările lor finite:
Înlocuind aceste expresii în (1.49), obținem un sistem de ecuații diferențiale:
(pentru i = 1) și yn (pentru i = n - 1) sunt luate din condițiile limită (1.42):
În practică, condițiile limită sunt adesea stabilite într-o formă mai generală (1.38):
În acest caz, condițiile de limită trebuie să fie reprezentate și în forma diferențială prin aproximarea derivatelor Y '(0) și Y' (1) prin relații finite-diferență. Dacă se utilizează diferențe unilaterale (modelul corespunzător este prezentat în Figura 1.7a), pentru care derivatele sunt aproximate cu prima ordine de acuratețe, atunci condițiile de limită a diferenței vor lua forma
Din aceste relații, valorile y 0, yn sunt ușor de găsit.
Cu toate acestea, de regulă, este preferabil să aproximăm derivații care apar în (1.52) cu a doua ordine de acuratețe prin intermediul diferențelor centrale:
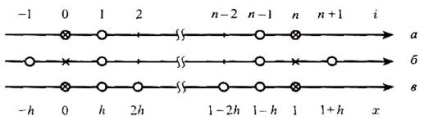
Fig. 1.7. Apropierea condițiilor limită
Aceste expresii includ valorile funcției grilei și yn + 1 în așa-numitele noduri fictive x = 1-h și x = 1 + h situate în afara segmentului considerat (Fig.1.7, b). În aceste noduri, trebuie de asemenea găsite valorile funcției dorite. În consecință, numărul de valori necunoscute ale funcției rețelei este mărit cu două. Pentru a închide sistemul, două ecuații diferențiale (1,51) sunt atrase pentru i = 0, i = n.
Este posibil să se aproximeze condițiile limită cu ordinea a doua într-un mod diferit (a se vedea figura 1.7, c). În acest caz, sunt utilizate aproximări:
Astfel, soluția problemei valorii limită pentru o ecuație diferențială este redusă la rezolvarea unui sistem de ecuații algebrice de formă (1.51). Acest sistem este liniar sau neliniar, în funcție de faptul dacă ecuația diferențială este liniară sau neliniară (1.41). Metodele de rezolvare a unor astfel de sisteme au fost luate în considerare anterior.
cu condițiile limită ale formularului
Se împarte intervalul [0,1] în părți cu un pas constant h folosind noduri. Aproximăm al doilea derivat Y2 prin relația finită-diferență (1.50). În acest caz, valorile funcției necunoscute la nodurile Y (xi) sunt aproximativ înlocuite cu valorile corespunzătoare ale funcției de rețea yi. Ecuația de scriere (1.54) la fiecare nod folosind aproximările indicate, obținem
Fie pi și fi cantitățile, respectiv. După transformări simple, reducem ultima egalitate la formă
Am obținut un sistem de ecuații liniare n-1, numărul cărora coincide cu numărul de valori necunoscute ale funcției rețelei la noduri. Valorile sale la capetele intervalului sunt determinate de condițiile limită (1.55):
Rezolvind sistemul de ecuații (1.56) cu condiția pentru condițiile (1.57), găsim valorile funcției rețelei, care sunt aproximativ egale cu valorile funcției necesare. Arătăm că există o astfel de soluție și converge la o soluție exactă ca h → 0.
Pentru a demonstra existența unei soluții, considerăm sistemul ecuațiilor liniare (1.56). Matricea sa este tridigonală; Pe diagonala principală sunt elementele. Deoarece p (x)> 0, pi> 0 și elementele diagonale ale matricei predomină asupra celorlalte, deoarece în fiecare rând, modulele acestor elemente sunt mai mari decât suma modulelor celorlalte două elemente, fiecare fiind egală cu una. Când această condiție este îndeplinită, soluția sistemului de ecuații liniare există și este unică.
În ceea ce privește convergența soluției, se afirmă următoarea afirmație.
Aprobarea. Dacă funcțiile p (x) și f (x) sunt de două ori continuu diferențiate, atunci pentru h → 0 soluția diferențială converge uniform la cea existentă cu viteza O (h2).
Aceasta este o condiție suficientă pentru convergența metodei diferenței finite pentru problema valorii limită (1.54), (1.55).
Un sistem de ecuații algebrice liniare (1.56) cu o matrice tridiagonală poate fi rezolvat printr-o metodă de ștergere. În acest caz, condiția p (x)> 0 asigură îndeplinirea condiției de stabilitate pentru rulare.
Această metodă este, de asemenea, utilizată în practică pentru p (x)<0, хотя успешный результат заранее предвидеть трудно. Для оценки получаемого решения в этом случае необходимо провести расчеты для разных значений шага (не менее трех) и убедиться в том, что полученные значения функции в одних и тех же узлах близки между собой и разность их уменьшается, что говорит о стремлении решения к некоторому пределу при h → 0.
Am considerat cel mai simplu caz de ecuație liniară. Este mult mai dificil să rezolvăm problemele neliniare. Considerăm problema limită-valoare pentru o ecuație de ordinul doi:
Folosind metoda diferenței finite, obținem un sistem de ecuații diferențiale neliniare
În teoria schemelor de diferențe se demonstrează că soluția diferenței determinată de ecuațiile diferențiale (1.59) converge la soluția exactă ca h → 0. O condiție suficientă pentru convergență are forma
Sistemul de ecuații algebrice neliniare (1.59) poate fi rezolvat prin metode iterative. Pentru ao rezolva, folosim și metoda de linearizare, adică Reducerea soluției unui sistem neliniar la soluția unei secvențe de sisteme de ecuații algebrice liniare.
Fie soluția sistemului (1.59) găsită pe k-iterație. Apoi, înlocuind valorile cunoscute în partea dreaptă a sistemului (1.59), obținem
În consecință, am ajuns la soluția unui sistem de ecuații algebrice liniare în raport cu valorile lui yi la iterația (k + 1). Deoarece matricea acestui sistem este tridiagonală, se poate folosi o metodă de ștergere pentru a rezolva problema la fiecare iterație. Este necesar doar să se specifice anumite aproximări inițiale; valorile y0, yn sunt determinate de condițiile limită (1.60).
Trebuie remarcat că convergența acestui proces iterativ este destul de lentă. O condiție suficientă pentru convergență are forma
Această condiție, precum și condiția (1.61), impun restricții pe partea dreaptă f (x, Y) a ecuației inițiale (1.58).
Articole similare
Trimiteți-le prietenilor: