Regiunea numerelor complexe face posibilă luarea în considerare a unor cazuri complexe atunci când se extrag rădăcini de grad mai mare de 2.
Știm deja că $ \ sqrt $ este +1 sau -1, $ \ sqrt $ este + i sau -i.

Și care este rădăcina a patra a lui +1 ($ \ sqrt [4] $)? Evident, (+1) x (+1) x (+1) x (+1) = + 1, adică +1 reprezintă una dintre rădăcinile puterii a patra de +1. În același mod, (-1) x (-1) x (-1) x (-1) = + 1, adică -1, este de asemenea una dintre rădăcinile puterii a patra +1. Dar nu am atins toate opțiunile încă. Cât despre expresia $ (+ i) \ times (+ i) \ times (+ i) \ times (+ i) $? Rezultatul multiplicării $ (+ i) \ times (+ i) $ este -1. Prin urmare, $ (+ i) \ times (+ i) \ times (+ i) \ times (+ i) = (-1) \ times (-1) = + 1 $. Aceasta înseamnă că + i este rădăcina a treia a puterii a patra de +1. În mod similar, putem arăta că -i este rădăcina a patra a puterii a patra de +1.
Prin urmare, problema noastră are următorul răspuns: ($ \ sqrt [4] $) = + 1, -1, + i, -i. În mod similar, putem arăta că ($ \ sqrt [4] $) egal cu $ + \ sqrt $, $ - \ sqrt $, $ + \ sqrt $ sau $ - \ sqrt $, adică, această problemă are patru soluții echivalente .
Și ce este $ \ sqrt $? Răspunsul este simplu. ($ \ sqrt $) este un număr care, înmulțit de el însuși, dă i. Prin urmare, ($ + \ sqrt $) x ($ + \ sqrt $) = + i Prin urmare, $ (+ \ sqrt) \ ori (- \ sqrt) \ ori (+ \ sqrt) \ ori (- \ sqrt) = ( + i) \ ori (+ i) = -1 $.
În consecință, ($ + \ sqrt $) este una dintre rădăcinile patrulea grad (-1), celelalte rădăcini sunt $ - \ sqrt $, $ + \ sqrt $ și $ - \ sqrt $.
În exact același fel, se poate arăta că orice număr are rădăcini de gradul patru.
Am arătat că fiecare număr are două rădăcini pătrate și patru rădăcini de gradul al patrulea. De asemenea, putem presupune că fiecare număr are trei rădăcini de gradul trei, cinci rădăcini de gradul cinci, șase rădăcini de gradul al șaselea, patruzeci și cinci de rădăcini de gradul patruzeci și cinci și așa mai departe. Această afirmație este absolut adevărată, dar pentru ao dovedi, avem nevoie de un aparat matematic complex pe care nu-l avem, așa că deocamdată, să-l considerăm drept.
Adevărat, putem verifica această afirmație pentru o rădăcină a gradului trei. Ce este, de exemplu, rădăcina unui cub de 1, sau ($ \ sqrt [3] $)? Mai întâi, (+1) x (+1) x (+1) = + 1, adică +1 este una dintre rădăcinile cubice de 1.
Și ce alte două sunt egale? Să trecem la zona numerelor negative. (-1) x (-1) x (-1) = (+ 1) x (-1) = -1.
Astfel, -1 nu este rădăcina cub 1. Mai mult decât atât, se poate arăta că nici un număr real, și nici unul imaginar (fie +1 sau -1) ridicată la puterea a treia, aceasta nu duce la + 1 .
Deci, există doar o rădăcină, iar celelalte două pur și simplu nu există?
Aceste două rădăcini există, dar în regiunea numerelor complexe. Acum dăm semnificația lor și puteți verifica ce sunt egale cu aceste numere, ridicate într-un cub. Celelalte două rădăcini cub de 1 + - este ($ - \ frac12 + \ frac12 \ sqrt $) și ($ - \ frac12- \ frac12 \ sqrt $). Să verificăm această declarație.
Dacă ($ - \ frac12 + \ frac12 \ sqrt $) - una din rădăcini cubi de unul, aceasta înseamnă că ($ - \ frac12 + \ frac12 \ sqrt $) 3 sau $ (- \ frac12 + \ frac12 \ sqrt) \ ori (- \ frac12 + \ frac12 \ sqrt) \ times (- \ frac12 + \ frac12 \ sqrt) $ este egal cu 1.
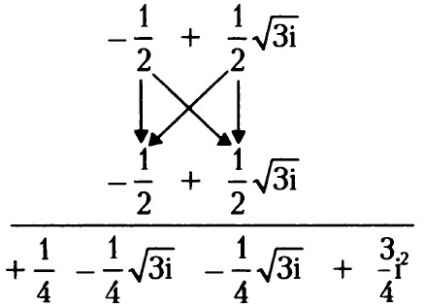
Două rezultat intermediar imaginar poate fi pliat, suma numerelor ($ - \ frac14 \ sqrt $) și ($ - \ frac14 \ sqrt $) egal cu ($ - \ frac12 \ sqrt $). În ceea ce privește $ \ frac34i $ 2, atunci acesta este un număr real egal cu $ - \ frac34 $. Acum, se adaugă cele două componente reale ale expresiei: $ \ frac14- \ frac34 = - \ frac12 $, astfel încât rezultatul înmulțirii $ - \ frac12- \ frac12 \ sqrt $.
Acest rezultat trebuie să fie înmulțit din nou cu ($ - \ frac12 + \ frac12 \ sqrt $).
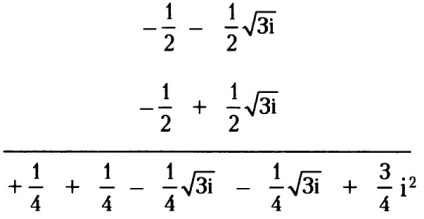
Cele două componente imaginare ale acestei expresii ($ - \ frac14 \ sqrt $) și ($ - \ frac14 \ sqrt $) se adaugă la 0, astfel încât acestea pot fi neglijate. Numărul $ \ frac34i $ 2 este un număr real, deoarece і 2 = -1, adică $ \ frac34i $ 2 = $ \ frac34 $. Adăugați la $ \ frac34 $ rezultatul intermediar rămas $ \ frac14 $ și obțineți 1. Astfel, ($ - \ frac12 + \ frac12 \ sqrt $) 3 este egal cu 1.
În același mod, se poate ridica la a treia putere numărul ($ - \ frac12- \ frac12 \ sqrt $) 3:
În același mod, putem arăta că numărul -1 are trei rădăcini de gradul trei, dintre care două sunt complexe. trei rădăcini cubice și numerele i și i.
Materiale pe tema:
Trimiteți-le prietenilor:
Trimiteți-le prietenilor: