




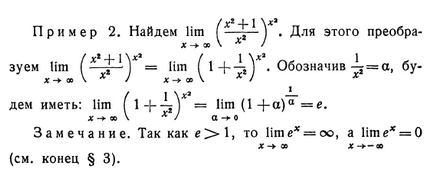
Proprietățile limitelor În toate exemplele prezentate mai sus, nu am găsit limitele, dar am demonstrat că un astfel de număr reprezintă limita unei funcții date în condițiile indicate. În mod firesc, se pune întrebarea cum să găsim numărul în legătură cu care vom continua să dovedim că este limita unei funcții date. Această problemă este aproape întotdeauna foarte dificilă, mai ales dacă decurgem de la definirea limitei. Pentru a simplifica această sarcină, de obicei folosim anumite proprietăți ale limitelor, la expunerea cărora continuăm. Proprietățile date vor fi explicate pe exemple, iar dovezile nu vor fi date. Dovezile pot fi găsite în cursuri mai complete, de exemplu: NS Piskunov, "Calculul diferențial și integrat" sau Tarasov, NP "Un curs în matematică superioară". Proprietatea 1. Valorile limită ale anumitor funcții este egală cu suma limitelor fiecăreia dintre aceste funcții, și anume. E. Lim [/ (*) + q> (*)] «Ix / (*) + liră. x - * a x a x -a În formularea acestei proprietăți, precum și în cele ce urmează, se presupune că toate limitele sunt calculate în aceleași condiții. Exemplu 1. Să găsim lim
nu știu că X o X Remark. Formularea proprietății 1 spune despre sumă, dar din moment ce diferența poate fi întotdeauna scrisă ca sumă, atunci proprietatea 1 se extinde și la diferența. sin x - x * Exemplul 2. Să găsim limita lim -. X o * = Ca + xn), apoi aplicând proprietatea 1, obținem lim X lim - * - O * X - + Q L J L Proprietate 2. Funcția limită care păstrează aceeași valoare, egală cu această valoare. Această proprietate este formulată diferit: limita constantei este egală cu această constantă. Exemplul 3. Să găsim limita lim [sin ** + cos * x]. i x - 2 Deoarece sin * x + cos x pentru orice valoare a lui x este 1, cazul în care funcția rămâne constantă este cazul aici, deci lim [sin * x + cos * x] = 1. 1 £ - r Exemplul 4. Să găsim limita lim 7,5. De la postul 7.5
este x-independent și nu depinde de x, atunci lim 7,5 = 7,5. X și proprietatea 3. Limita produsului a două funcții este egală cu produsul limitelor acestor funcții. m- și x * sin X + sin * X Exemplul 5. Se constată limita lim -j-. În exemplul 1 din această secțiune sa arătat că lim - = 1, iar în §2, lim = 1. Aplicând proprietatea X - + Q X X - * Q X la proprietatea 3, obținem x * sin x -f păcatul * x Yx * -f sin x x sin x
\ lim X - t. x9 + păcat * păcat *. t = lim - lim - = 1.1 = 1. X -> 0 X X Q X Deși numai două funcții sunt menționate în declarația proprietății 3, aceeași proprietate poate fi utilizată pentru un număr mai mare de factori. n și m 1 * T4 (sin * -f- cos * x) păcat dc! 0 Exemplul 6. Găsiți lim ---- L-. Această expresie L x tensiune J poate fi reprezentat ca produsul a doi factori: [4 (SIN1 x + cos *)] și aplicând proprietatea 3, aplicăm aceeași proprietate la primul factor, obține lim [4 (sin * jc + cos2 x )] lim = XQX 0 * = lim 4 lim (sin * x + cos1 x) lim = 4 • N = 4. X - * x Proprietatea 4. Limita coeficientului a două funcții este egală cu coeficientul împărțirii limitei divizibile la limita divizorului, cu condiția ca limita divizorului să nu fie zero. x -4-2 Exemplul 7. Să găsim limita lim -. Deoarece, ca lim (x + 2) = 4, lim (x - 1) = 1, avem din proprietatea 4 x x x r că 1 *
= - = 4. x-t * -1 1 Dacă limita divizorului este zero, atunci limita coeficientului poate fi egală cu orice număr în funcție de divizibil. Să dăm câteva exemple. Exemplul 8. Luați în considerare limita lim -, unde m este un număr întreg X x> 0. În acest exemplu, limita divizorului este zero, deoarece lim jce = lim x-lim x »limx = 0. XX - * • 0 X O X Să examinăm eventualele cazuri particulare. Dacă / "= 1, atunci lim lim = a lim - • lim - = oo Y« Y * x. X X 0 X - * 0 A X -> 0 X - * 0 A (a se vedea secțiunea 5 din § 1 și explicația semnului de la § 2, § 3). Dacă m = 3, atunci lim - lim a - a. x „R s Dacă m = 5, atunci lim - = lim AH1 = o lim x = 0. X O * X -► 0 pentru x Rețineți că determinarea limitei coeficientului de două funcții, în cazul în care limitele și divizorul și dividendului în același timp sunt egale cu zero, este cea mai des întâlnită problemă și teoretic una dintre cele mai importante. Dar în acest caz proprietatea 4 nu funcționează. Proprietatea 5 (o proprietate importantă a limitei). Dacă punctul M se deplasează în mod arbitrar de-a lungul axei x, se apropie de punctul P ca limita sa și punctul P nu coincide cu originea, singurele două cazuri: 1) în cazul în care F are abscisă pozitiv, punctul M, cu ceva timp are, de asemenea pozitiv abscisa; 2) dacă P are o abscisă negativă, atunci punctul M dintr-un moment are o abscisă negativă. Prin urmare, dacă limita nu este zero, atunci pentru o perioadă de timp semnele limitei și valoarea pre-limită coincid. § 5. Limita lim (1 + • *) *. Numărul e X o 1 Luați în considerare funcția (1 + x) *. Dacă x tinde la zero, atunci conținutul unității de abordare a consolei. Dacă x nu este egal cu zero, atunci brațul nu va fi egal cu unul; Mai mult, dacă x este mai mare decât zero, atunci brațul este mai mare decât unul, dacă x este mai mic decât zero, atunci brațul este mai mic decât unul. 1 Considerăm lim (1 + x) x. Nu este clar ce va fi egal cu, deoarece pentru un număr mai mare decât unul se ridică la un nivel pozitiv și pentru n un număr mai mic decât unul este ridicat la un grad negativ. Cu toate acestea, se poate demonstra că această limită există. Acest lucru este dovedit în cursuri detaliate. Numărul egal cu această limită este notat cu litera e. Astfel, numărul e este lim (1 + x) *. X o Numărul e este un număr irațional, valoarea sa aproximativă (cu o precizie de o mie) 2,718. Apare în matematică la fel de des ca și numărul i. S-a dovedit a fi foarte convenabil să se ia numărul e ca baza a logaritmilor. Logaritmii cu baza e se numesc logaritmi naturali. Ele sunt marcate cu semnul In. Aceste logaritme sunt folosite în principal în întrebări teoretice. Exemplul 1. Să găsim Noi denotăm prin x = x, avem ca n -> oo, x -> 0. Prin urmare, (X * + 1 -). Pentru această transformare - Noi denotăm prin lim = lim 1. 1. Denotând ξ = bu avem: lim (\ + \) = lim (l + a) a = ε. Deoarece ε> 1, atunci lim ex = oo, și lim ex = 0 χ ω X (vezi sfârșitul §3).
Articole similare
Trimiteți-le prietenilor: