Definiția. Dacă funcția f (x) este definită în intervalul [a, b], este continuă în fiecare punct al intervalului (a, b), este continuă în punctul a, în punctul b este continuă, atunci funcția f (x) [a, b].
Cu alte cuvinte, funcția f (x) este continuă pe intervalul [a, b] dacă sunt îndeplinite trei condiții:
Pentru funcțiile care sunt continue într-un interval, luăm în considerare câteva proprietăți pe care le formăm sub forma următoarelor teoreme, fără a face dovezi.
Teorema 1. Dacă funcția f (x) este continua pe intervalul [a, b], atunci se ajunge la acest segment de minim și de valoarea sa maximă.
Această teoremă afirmă (Figura 1.15) că pe segmentul [a, b] există un punct x1. că f (x1) ≤ f (x) pentru orice x din [a, b], și că există un punct x2 (x2 [a, b]) astfel încât
Valoarea f (x1) este cea mai mare pentru o funcție dată pe [a, b], iar f (x2) este cea mai mică. Denumim prin f (x1) = M, f (x2) = m. Deoarece f (x) satisface inegalitatea :. atunci obținem următorul corolar din Teorema 1.
Corolar. Dacă funcția f (x) este continuă într-un interval, atunci ea este mărginită pe acest interval.
Teorema 2. Dacă funcția f (x) este continua pe intervalul [a, b] și la punctele finale ia valori de semne diferite, atunci există un interval intern punct x0 [a, b], în care funcția este egal cu 0, adică, .
Această teoremă afirmă că graficul funcției y = f (x) care este continuu pe intervalul [a, b] intersectează axa Ox cel puțin o dată dacă valorile f (a) și f (b) au semne opuse. Astfel, (figura 1.16), f (a)> 0, f (b) <0 и функция f(x) обращается в 0 в точках x1. x2. x3 .
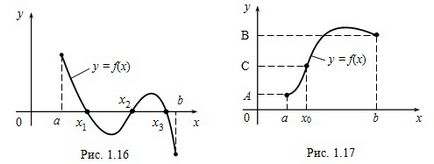
Teorema 3. Fie funcția f (x) continuă pe intervalul [a, b], f (a) = A, f (b) = B și
A ≠ B. (Figura 1.17). Apoi, pentru orice număr C cuprins între numerele A și B, există un punct interior x0 al lui [a, b] astfel încât f (x0) = C.
Corolar. Dacă funcția f (x) este continuă pe intervalul [a, b], m este cea mai mică valoare a f (x), M este cea mai mare valoare a funcției f (x) din intervalul [a, b] orice valoare de m, cuprinsă între m și M și, prin urmare, intervalul [m, M] este setul tuturor valorilor funcției f (x) din intervalul [a, b].
Rețineți că dacă o funcție este continuă pe interval (a, b) sau are în interval
[a, b] al punctului de discontinuitate, atunci Teoremele 1, 2, 3 pentru ca o astfel de funcție să înceteze să mai fie adevărată.
În concluzie, considerăm teorema privind existența unei funcții inverse. Ne amintim că un interval este înțeles ca un segment sau un interval, sau un interval de jumătate este finit sau infinit.
Teorema 4. Fie f (x) continuu pe intervalul X, mărim (sau micșorează) pe X și avem un interval de valori ale intervalului Y. Apoi pentru funcția y = f (x) există o funcție inversă x = (Y), definită pe intervalul Y, este continuă și în creștere (sau descrescătoare) pe Y cu setul de valori ale lui X.
Notă. Fie funcția x = (Y) este inversa funcției f (x). Deoarece argumentul este de obicei marcat cu x și funcția este notată cu y, vom scrie funcția inversă în forma y = # 966; (x).
Exemplul 1. Funcția y = x 2 (fig. 1.8, a) pe un set de X = [0, + ∞) este continuă, în creștere și are o multitudine de valori ale lui Y = [0, + ∞). Funcția y = x 2 este funcție inversă x = √y (Fig. 1.8, b) și după redenumirea variabilelor x y =. definit, continuu și în creștere pe X.
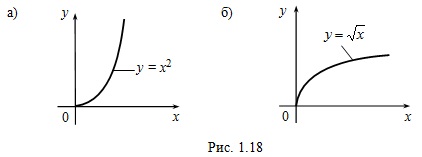
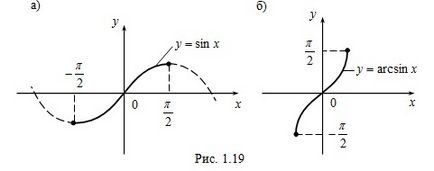
Exemplul 2. Funcția y = sinx (fig. 1.19, a) continuă și creșterea intervalului și are o pluralitate de intervalul [-1, 1] valoare, deci are funcția inversă y = arcsinx (fig. 1.19, b) un anumit, continuu și crescând pe segmentul [-1, 1] și având un set de valori
Rețineți că graficele funcțiilor inverse reciproce sunt simetrice în raport cu linia dreaptă y = x. Propunem să construim grafice de funcții inverse:
1. y = cosx, y = arccosx;
2. y = tgx, y = arctgx;
3. y = ctgx, y = arcctgx;
4. y = e x. y = lnx.
Articole similare
Trimiteți-le prietenilor: