Regula de multiplicare a matricei
Să presupunem că 2 matricea A (m x n) și B (n × l), iar numărul de coloane ale matricei A este numărul de rânduri ale matricei B. Apoi, matricea C (m × l) cu elementele. (I-lea și anume rând de matricei A, înmulțit cu un scalar pe coloană j-a matricei B, dă elementul cij lea al matricei C, în picioare în rândul i-lea și coloana j-a).
. .
Proprietatea unui sistem de ecuații liniare care conține ecuația trivială.
Ecuația trivială este o ecuație în care coeficienții tuturor termenilor necunoscuți și liberi sunt zero.
Teoremă: Un sistem de ecuații liniare care conține o ecuație trivială este echivalent cu același sistem fără o ecuație trivială.
Dovada: Luați în considerare LMC (1) și aceeași LMC (2), dar fără ecuația trivială.
Fie vectorul o soluție a sistemului (1), atunci acest vector este, de asemenea, o soluție a sistemului (2).
În schimb, permiteți vectorului să fie o soluție a sistemului (2). pentru că Un vector n-dimensional L este, de asemenea, o soluție a ecuației triviale, atunci este o soluție a sistemului (1).
Astfel, un sistem de ecuații liniare care conține o ecuație trivială este echivalent cu același sistem fără o ecuație trivială.
Proprietatea de necunoscute gratuite în SLD permisă
SLP se numește rezolvată. dacă fiecare ecuație a sistemului conține cel puțin un necunoscut rezolvat.
Teorema: dacă într-un SLD permis (4), dă-i necunoscute libere valori arbitrare. t. e .. atunci există o soluție unică a acestui sistem sub forma unui vector n-dimensional K pentru care valorile coordonatelor corespunzătoare celor necunoscute sunt egale.
Îl substituim în sistem (4). Apoi necunoscutele rezolvate vor lua valori astfel:
Deoarece vectorul transformă fiecare ecuație a sistemului (4) în egalitate numerică exactă, este o soluție a acestui sistem. Astfel, este demonstrată existența unei soluții a sistemului (4).
Să dovedim unicitatea unei astfel de soluții. Permiteți unui vector cu aceleași valori de necunoscute libere să fie, de asemenea, o soluție a sistemului (4). Apoi îl înlocuim în sistem (4), obținem:
Comparând (5) și (6), vedem asta. Astfel, se demonstrează că există o soluție unică a sistemului (4) cu valori date de necunoscute libere.
1) Deoarece valorile necunoscutelor libere pot fi specificate într-un număr infinit de moduri mari, sistemul (4) este incert.
2) SLD permis este întotdeauna compatibil. În acest caz, este definită. dacă m = n. adică numărul de ecuații este egal cu numărul de necunoscute și nu este definit. dacă numărul de ecuații este mai mic decât numărul de necunoscute, adică m Soluția sistemului de ecuații omogene Se consideră că o ecuație liniară este omogenă. dacă termenul său liber este zero și este altfel neomogen. Un sistem format din ecuații omogene este considerat omogen și are forma generală: 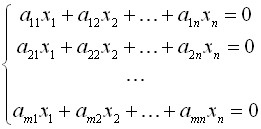
Teorema. Un sistem omogen de ecuații liniare are o soluție nonzero dacă și numai dacă rangul său este mai mic decât numărul de necunoscute.
Dovada: Să presupunem că un sistem al cărui rang este egal cu. are o soluție nonzero. Evident, nu depășește. În cazul în care sistemul are o soluție unică. Deoarece sistemul de ecuații liniare omogene are întotdeauna o soluție zero, soluția zero este singura soluție. Astfel, soluțiile non-zero sunt posibile numai atunci când.
Corolarul 1: Un sistem omogen de ecuații în care numărul de ecuații este mai mic decât numărul de necunoscuți are întotdeauna o soluție nonzero.
Dovada: În cazul sistemului de ecuații. atunci rangul sistemului nu depășește numărul de ecuații. și anume . Astfel, condiția este satisfăcută și, prin urmare, sistemul are o soluție nonzero.
Corolarul 2: Un sistem omogen de ecuații cu necunoscute are o soluție nonzero dacă și numai dacă determinantul său dispare.
Dovada: Să presupunem un sistem de ecuații lineare omogene a căror matrice cu determinant. are o soluție nonzero. Apoi teorema sa dovedit. Aceasta înseamnă că matricea este degenerată; .
Exemple de sisteme de vectori dependenți liniar și independenți liniar de vectori
1) Se spune că un sistem de vectori m-dimensionali este dependent de liniaritate. dacă sistemul de ecuații liniare (1) are soluții nonzero. Dacă sistemul (1) nu are soluții non-zero, atunci sistemul de vectori dat este independent de liniaritate.
2) Se spune că un sistem de vectori m-dimensionali este dependent de liniaritate. dacă există un vector nonzero. că relația liniară (2) este îndeplinită. Dacă din orice legătură a formularului (2) rezultă că. atunci se spune că sistemul de vectori este liniar independent.
Exemple de probleme de programare liniară: ieșire, rație, transport, portofoliu de valori mobiliare.
Articole similare
-
Investigarea stabilității sistemelor de comandă automată liniară 1
-
Investigarea stabilității sistemelor liniare de comandă automată
Trimiteți-le prietenilor: