Lecție și prezentare pe temele: "Logaritme naturale: baza logaritmului natural, logaritmul numărului natural"
Care este logaritmul natural?
Băieți, în ultima lecție am învățat un nou număr special - e. Astăzi vom continua să lucrăm cu acest număr.
Noi toți logaritmi studiate și știm că la baza jurnalului poate fi un set de numere care sunt mai mari decât 0. Astăzi ne uităm, de asemenea, la jurnal, baza, care este numărul de e. Acest jurnal se numește logaritmul natural. Are propriul său record: $ \ ln $ este logaritmul natural. O astfel de înregistrare este echivalentă cu scrierea: $ \ log_e = \ ln $.
Funcțiile exponențiale și logaritmice sunt inverse, atunci logaritmul natural este invers la funcția: $ y = e ^ x $.
Funcțiile inverse sunt simetrice în raport cu linia $ y = x $.
Să trasăm logaritmul natural prin reflectarea funcției exponențiale față de linia $ y = x $.
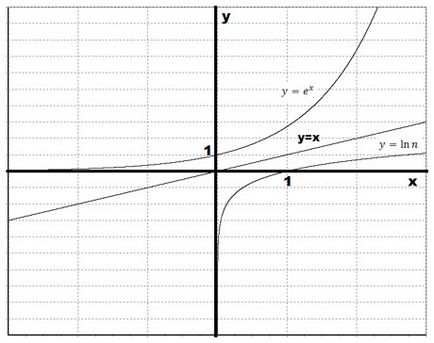
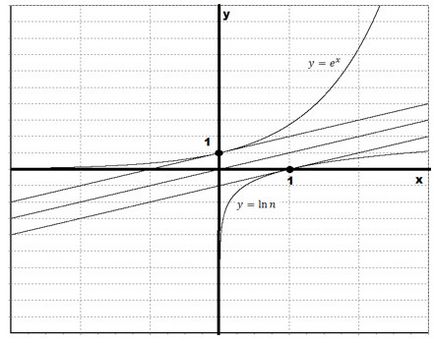
Este de remarcat faptul că unghiul de înclinare a tangentei la graficul funcției $ y = e ^ x $ la punctul (0; 1) este de 45deg. Apoi, unghiul de înclinare al tangentei la graficul logaritmului natural la punctul (1; 0) va fi, de asemenea, egal cu 45deg. Ambele aceste tangente vor fi paralele cu linia $ y = x $. Să schițăm tangentele:
Proprietățile funcției $ y = \ ln $
1. $ D (f) = (0; + ∞) $.
2. Nu este nici măcar ciudat.
3. Se dezvoltă în întreaga definiție.
4. Nu este limitat mai sus, nu este limitat mai jos.
5. Nu există valoare cea mai mare, nu există valoare minimă.
6. Este continuă.
7. $ E (f) = (- ∞; + ∞) $.
8. A urcat.
9. Diferențiat peste tot.
În cursul matematicii superioare se dovedește că derivatul funcției inverse este inversul derivatului unei funcții date.
Aprofundarea în dovadă nu are prea mult sens, să notăm doar formula: $ y '= (\ ln)' = \ frac $.
Un exemplu.
Calculați valoarea derivatului funcției: $ y = \ ln (2x-7) $ la punctul $ x = 4 $.
Soluția.
În general, funcția noastră este o funcție $ y = f (kx + m) $, putem calcula derivatele acestor funcții.
$ y '= (\ ln)' = \ frac $.
Calculam valoarea derivatului la punctul cerut: $ y '(4) = \ frac = 2 $.
Răspuns: 2.
Un exemplu.
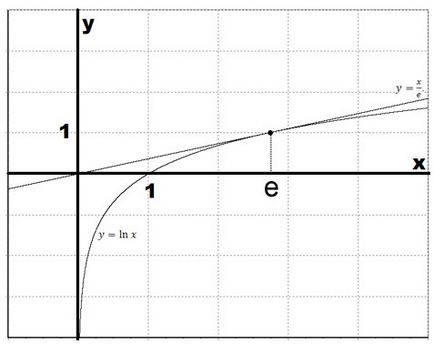
Desenați o tangență la graficul funcției $ y = ln $ la punctul $ x = e $.
Soluția.
Ecuația tangentei la graficul funcției la punctul $ x = a $ este bine amintită.
$ a = f (a) + f '(a) (x-a) $.
Calculați secvențial valorile solicitate.
$ a = e $.
$ f (a) = f (e) = \ ln = 1 $.
$ f '(a) = \ frac = \ frac $.
$ y = 1 + \ frac (x-e) = 1 + \ frac- \ frac = \ frac $.
Ecuația tangentei la punctul $ x = e $ este o funcție $ y = \ frac $.
Să complotăm logaritmul natural și tangenta.
Un exemplu.
Examinați funcția pentru monotonie și extrema: $ y = x ^ 6-6 * ln $.
Soluția.
Domeniul funcției $ D (y) = (0; + ∞) $.
Să găsim derivatul unei funcții date:
$ y '= 6 * x ^ 5- \ frac $.
Derivatul există pentru toate x din domeniul definiției, atunci nu există puncte critice. Să găsim punctele staționare:
$ 6 * x ^ 5- \ frac = 0 $.
$ \ frac = 0 $.
$ 6 * x ^ 6-6 = 0 $.
$ x ^ 6-1 = 0 $.
$ x ^ 6 = 1 $.
$ x = ± 1 $.
Punctul $ x = -1 $ nu aparține domeniului definiției. Apoi avem un punct staționar $ x = 1 $. Observăm intervalele de creștere și de scădere:
Punctul $ x = 1 $ este un punct minim, apoi $ y_min = 1-6 * \ ln = 1 $.
Răspuns: funcția scade pe intervalul (0; 1); funcția crește pe raza $ [1; + ∞) $. $ y_min = 1 $.
Băieți, putem calcula derivatele logaritmului natural și funcția exponențială. Dar nu știm încă cum să calculăm derivatul oricărui alt logaritm și orice funcție exponențială.
Luați în considerare funcția exponențială $ y = a ^ x $.
Amintiți-vă proprietatea: $ c ^> = b $.
Apoi: $ a = e ^ $.
$ a ^ x =)> ^ x = e ^ $.
Gasim derivatul: $ (a ^ x) '= (e ^)' = \ ln * e ^ = \ ln * a ^ x $.
Derivatul funcției exponențiale este egal cu: $ (a ^ x) '= \ ln * a ^ x $.
Trecem la logaritmuri, folosim formula pentru trecerea la o bază nouă:
$ \ log_a = \ frac> $.
Să găsim derivatul: $ (\ log_a) '= (\ frac>)' = \ frac * (\ ln) '= \ frac * \ frac = \ frac $.
Derivatul logaritmului față de baza a numărului x este egal cu:
$ (\ log_a) '= \ frac $.
Probleme privind logaritmul natural pentru auto-soluționare
1. Calculați valoarea derivatului funcției $ y = \ ln $ în punctul $ x = 3 $.
2. Calculați valoarea derivatului funcției $ y = \ log_4 $ la punctul $ x = -2 $.
3. Găsiți ecuația tangentei la graficul funcției $ y = \ ln $ la punctul $ x = 2e $. Schematic trageți un grafic.
4. Investigați funcția ca monotonicitate și extremum: $ y = x ^ 8-4 * \ ln $.
Trimiteți-le prietenilor: