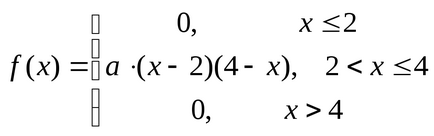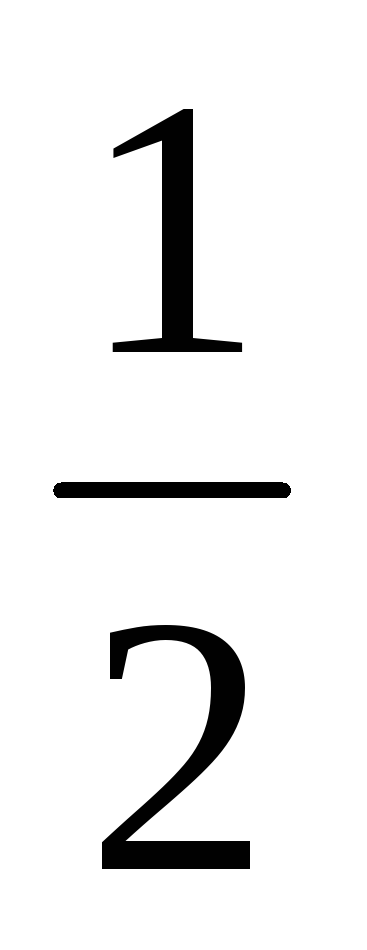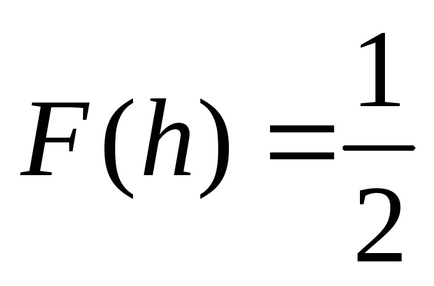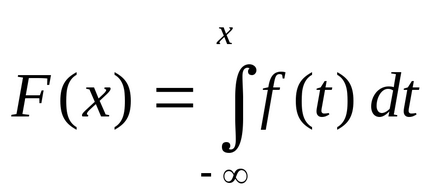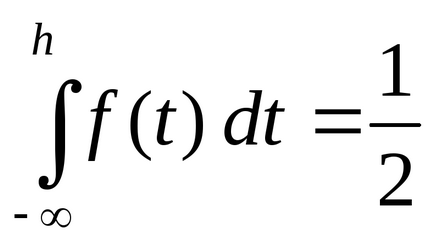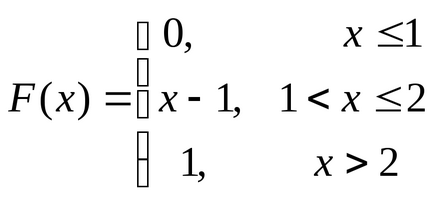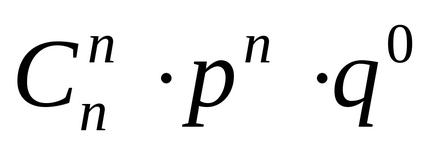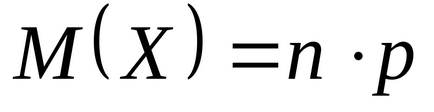Apoi, modul său presupune 2 valori: d (X) = 3 și d (X) = 5.
Fie X o variabilă aleatorie continuă cu densitatea de probabilitate f (x). Moda acest d.v. este punctul maxim al densității de probabilitate. Acest punct al maximului funcției f (x) se găsește prin metodele uzuale care utilizează derivatul.
Un exemplu. Având în vedere densitatea de probabilitate a nsv.
.
Găsiți valoarea parametrului a și a modului acestei variabile aleatorii.
Fie X o variabilă aleatorie continuă. Median SV X (notat cu h (X)) este un număr h. care divizează întreaga linie de numere în 2 intervale (-∞, h) și [h, + ∞). în care d.v. X cade cu probabilitate egală. Astfel, dacă mediana h (X) = h, atunci egalitatea
P (X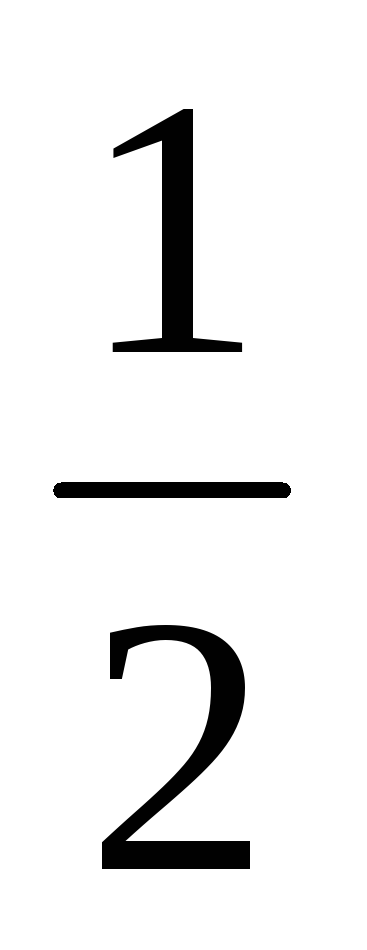
.
Reamintind că probabilitatea P (X
.
Dacă, totuși, nsv. Funcția de distribuție F (x) nu este dată. dar densitatea de probabilitate f (x). apoi reamintind expresia funcției de distribuție în termeni de densitate de probabilitate
. constatăm că valoarea h a medianului satisface ecuația
.
Mediana h (X) este o continuă sv. X este căutat din una din ecuațiile de mai sus (în funcție de ceea ce este dat: F (x) sau f (x)). Pentru variabilele aleatoare discrete, mediana nu este determinată.
Un exemplu. Găsiți mediana nsv X. dat de funcția sa de distribuție
.
Unele legi importante pentru distribuirea variabilelor aleatoare
Printre diversele legi de distribuție a variabilelor aleatoare, unele apar în aplicații cel mai des. Prin urmare, ei au obținut formule pentru calcularea caracteristicilor lor numerice: așteptarea matematică, variația, modul, mediana și un număr de altele. Să luăm în considerare unele dintre aceste legi de distribuție.
Legea distribuției binomiale
Printre legile de distribuție ale variabilelor aleatorii discrete, cea mai comună este distribuția binomială, cu care ne-am întâlnit deja atunci când am luat în considerare așa-numita schemă Bernoulli (numărul de apariții ale unui eveniment dintr-o serie de studii independente).
Variabila aleatoare discretă X este distribuită conform legii binomiale. dacă ia valori 0, 1, 2.n cu probabilități p0, p1. pn. care sunt calculate prin formula
,
unde parametrul de distribuție p este între zero și unitatea 0 ≤ p ≤ 1 și q = 1-p. Astfel, DS în X. distribuit conform legii binomiale, are următoarea lege de distribuție:
După cum sa menționat deja, în conformitate cu legea binomică, numărul succeselor din schema Bernoulli este distribuit. Să presupunem că sunt efectuate n probe independente, în fiecare dintre care poate apărea un eveniment A cu aceeași probabilitate p. Luați în considerare un rv. X este numărul de apariții ale evenimentului A în toate studiile n (ceea ce a fost denumit anterior numărul de succese). Atunci dv X este distribuit conform legii binomiale. Am găsit deja formule pentru așteptările matematice ale acestei variabile aleatoare, care sunt formule pentru așteptările matematice și varianța unei variabile aleatorii arbitrar distribuite conform schemei Bernoulli:
, .
Se găsește modul d (X) al variabilei aleatorii distribuite binomic X. cel mai probabil număr de succese din schema Bernoulli. Prin definiția modului, d (X) = k. dacă probabilitatea este cea mai mare între toate probabilitățile p0, p1. pn. Să găsim un număr k (acesta este un număr întreg negativa). Pentru astfel de k, probabilitatea pk nu trebuie să fie mai mică decât probabilitățile adiacente lui: pk-1≤pk≤pk + 1. Înlocuind pentru fiecare probabilitate formula corespunzătoare, obținem că numărul k trebuie să satisfacă dubla inegalitate:
.
Dacă scriem formule pentru numărul de combinații și facem transformări simple, putem observa că inegalitatea de stânga dă k≤ (n + 1) ∙ p. și dreapta k≥ (n + 1) ∙ p-1. Astfel, numărul k satisface dubla inegalitate (n + 1) ∙ p-1 ≤k≤ (n + 1) ∙ p. și anume aparține intervalului [(n + 1) ∙ p-1, (n + 1) ∙ p]. Deoarece lungimea acestui segment este în mod evident egală cu 1., atunci unul sau doi întregi pot intra în ea. Dacă numărul (n + 1) ∙ p este un număr întreg, atunci în segmentul [(n + 1) ∙ p-1, (n + 1) ∙ p] există 2 numere întregi situate pe capetele segmentului. Dacă numărul (n + 1) ∙ p nu este un număr întreg, atunci în acest segment există un singur număr întreg.
Astfel, dacă numărul (n + 1) ∙ p este un număr întreg, atunci modul de variație aleatorie distribuită binomic X ia 2 valori învecinate. d (x) = (n + 1) ∙ p-1 și d (X) = (n + 1) ∙ p. Dacă numărul (n + 1) ∙ p nu este un număr întreg, atunci modul de variabilă aleatorie distribuită binomial X este o valoare a d (X) = k. unde k este singurul întreg care satisface inegalitatea (n + 1) ∙ p-1 ≤k≤ (n + 1) ∙ p. Dacă ne amintim că înregistrarea [a] înseamnă a lua întreaga parte a numărului a. atunci în acest caz putem scrie d (X) = [(n + 1) ∙ p].
Un exemplu. Cubul este aruncat de 100 de ori. Care este cel mai probabil număr de depoziții ale celor șase?
Un exemplu. Probabilitatea ca țintă să cadă în țintă este de 0,7. Găsiți cel mai probabil număr de hit-uri pe țintă cu 30 de fotografii.
Un exemplu. Probabilitatea producerii unei părți defecte pe o mașină este de 0,06. Care este cel mai probabil număr de piese defecte dintr-un lot de 200 de piese prelucrate pe această mașină?
Un exemplu. Banca a emis 7 împrumuturi. Se știe că, în medie, 2 credite din 10 nu sunt returnate. Găsiți numărul mediu de credite nerevenite.
Articole similare
Trimiteți-le prietenilor: