Teoria grafică studiază obiectele matematice care descriu relațiile dintre elementele unui set finit.
Pentru o lungă perioadă de timp, problemele individuale ale teoriei grafurilor au apărut ca sarcini de divertisment ușor de formulat, dar din anumite motive au fost foarte greu de rezolvat. Dintre aceste probleme, problema celor șapte poduri Koenigsberg este cea mai cunoscută.
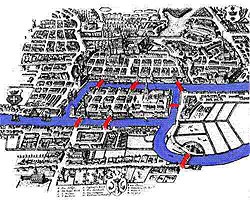
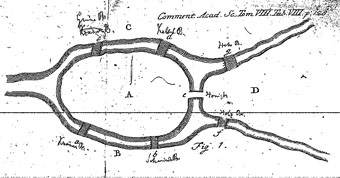
Sunt deosebit de încântat să vă amintesc această carte - am citit-o imediat, încă în franceză (pe care nu o știu) și l-am folosit în mod semnificativ în predarea matematicii. Astfel, terminologia și abordările noastre urmăresc, în esență, cartea lui Berg, deși acum există o mulțime de cărți care descriu teoria grafurilor interne și externe, teoretice și aplicate.
Definiția inițială pare descurajantă
Un număr este triplu. unde M este un set finit non-gol, N este un set finit, iar T este o hartă de la N la M × M.
Nu este clar de ce este necesar acest lucru. Acum ne vom da seama. Totul depinde de semnificația care se pune în aceste notații.
Elementele lui M sunt numite nodurile graficului. Setul de vârfuri nu trebuie să fie gol.
Elementele setului N sunt numite arce ale graficului. Maparea T asociază fiecare arc cu o pereche ordonată de vârfuri. Primul dintre acestea este numit începutul acestui arc, iar al doilea este numit sfârșitul arcului.
Și cel mai important lucru: graficul poate fi reprezentat grafic. comparați-le cu vârfurile unui punct, cercuri sau alte figuri și asociați liniile cu arce. Fiecare arc este reprezentat de o linie care pornește de la începutul acestui arc până la sfârșitul acestuia. Forma liniei și aranjarea vârfurilor din figură sunt arbitrare. Într-un fel, o direcție de la început până la sfârșit este indicată pe linie sau lângă ea.
Se spune că arcul este incidentul începutului și sfârșitului său, iar aceste două noduri sunt incidentale pentru arc. Cuvântul incidental înseamnă "inerent".
Setul de arce care intră într-un anumit vârf se numește stea. Este convenabil să vorbim despre steaua arcurilor de intrare și despre stelele arcurilor de ieșire.
Sub acest grafic este prezentat în patru moduri diferite.
O altă definiție determinată de particularitățile arcului 5.
Un arc al cărui început și sfârșit coincid se numește o buclă. Arc 5 este o buclă.
Să presupunem că ni se dă un grafic. Fie N un subset al lui N.
Un grafic este numit grafic grafic parțial.
În acest exemplu, dacă selectați N '=. atunci graficul parțial corespunzător va arăta așa cum este arătat în dreapta (absentul în graficul parțial al arcului este desenat în gri deschis). Iată un exemplu de subgraf al aceluiași grafic care corespunde lui M '= A, B, D>. graficul este numit calea simplă (a linkului k), dacă
1. | = | M ' - 1 = k.
2. Este posibilă enumerarea elementelor M 'prin numere de la 0 la k și elemente N' prin numere de la 1 la k. că pentru orice arc j N N 'egalitățile
num (j) = num (iEnd (j)) = num (iBeg (j)) + 1.
Astfel, definiția corespunde reprezentării noastre vizuale a căii: ea poate fi traversată în direcția indicată de săgeți de la vârful zero inițial la ultimul.
Un vârf cu un număr zero este numit începutul căii. iar ultimul vârf este sfârșitul căii.
A doua definiție. Calea cu săgețile "confuz", în care pe anumite secțiuni mergeți în direcția indicată.
Graficul este numit lanțul (al linkului k), dacă
1. | = | M ' - 1 = k.
2. Este posibilă enumerarea elementelor M 'prin numere de la 0 la k și elemente N' prin numere de la 1 la k. că pentru orice arc j N N 'au următoarele egalități
num (j) = num (iEnd (j)) = num (iBeg (j)) + 1.
sau
num (j) = num (iBeg (j)) = num (iEnd (j)) + 1.
Există două astfel de numerotări pentru lanț: oricare dintre vârfurile finale poate fi considerată ca fiind originea. Toate lanțurile de arc sunt împărțite în pozitive și negative - în care, trecând de la vârful inițial până la ultimul, mergem de-a lungul săgeții sau întâlnim săgeata. Vârfurile cu cel mai mic și cel mai mare număr sunt numite vârfurile extreme ale lanțului. Se spune că lanțul le conectează vârfurile extreme.
A treia definiție. "Calea închisă", care, contrar definiției căii, începutul și sfârșitul au coincis și informațiile despre acest vârf au fost uitate.
graficul este numit contur (link k), dacă
1. | = | M ' = k.
2. Este posibilă enumerarea elementelor M 'și elemente N' prin numere de la 1 la k. că pentru orice arc j N N 'egalitățile
num (j) = num (iEnd (j)) = num (iBeg (j)) + 1 modul k.
Numărul acestor numerotări este egal cu k - oricare dintre vârfuri poate fi considerat ca origine.
A patra definiție. Acest obiect combină proprietățile unui lanț și ale unui contur.
graficul este numit un ciclu (al linkului k), dacă
1. | = | M ' = k.
2. Este posibilă enumerarea elementelor M 'și elemente N' prin numere de la 1 la k. că pentru orice arc j N N 'au următoarele egalități
num (j) = num (iEnd (j)) = num (iBeg (j)) + 1 modul k.
sau
num (j) = num (iBeg (j)) = num (iEnd (j)) + 1 modul k.
Numărul acestor numerotări este 2 × k - oricare dintre vârfuri poate fi considerat ca origine, iar numărul poate fi luat în una din cele două direcții.
În prima definiție, am spus un mod simplu. deoarece este posibilă introducerea unei construcții mai complexe, o secvență de tranziții constând din arce care pot apărea mai mult decât o dată în secvență. Aceste tranziții trebuie să fie coordonate - începutul fiecărui arc, cu excepția primului, este sfârșitul celui precedent. Vertexele pot apărea, de asemenea, pe drum de mai multe ori.
Articole similare
-
Analiza uzi a inimii la informațiile copilului în care să facă prețul
-
Analiza pieței de alcool a rezultatelor rusiei din 2018 și prognoza pentru anul 2018
Trimiteți-le prietenilor: