Atenuarea oscilațiilor este scăderea amplitudinii oscilațiilor în timp, datorită pierderii de energie a sistemului vibrațional (de exemplu, conversia energiei vibraționale în căldură datorată frecării în sistemele mecanice). Atenuarea încalcă periodicitatea oscilațiilor, deoarece acestea nu mai sunt un proces periodic. Dacă atenuarea este mică, atunci putem folosi în mod condițional conceptul perioadei de oscilații - T (în figura 7.6 A0 este amplitudinea inițială a oscilațiilor).
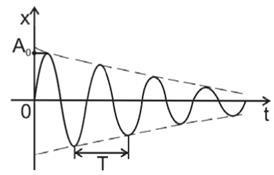
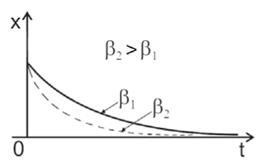
Figura 7.6 - Caracteristicile oscilațiilor amortizate
Oscilațiile mecanice amortizate ale pendulului de primăvară se produc sub acțiunea a două forțe: forța de elasticitate și forța de rezistență:
unde r este coeficientul de rezistență.
Folosind ecuația celei de-a doua legi a lui Newton, se poate obține:
Împărțim ultima ecuație cu m și introducem notația sau
unde # 946; coeficientul de amortizare, atunci ecuația ia forma
Această expresie este ecuația diferențială a oscilațiilor amortizate. Soluția acestei ecuații este
Aceasta implică natura exponențială a oscilațiilor amortizate, adică Amplitudinea oscilațiilor scade exponențial (figura 7.6):
Scăderea relativă a amplitudinii oscilațiilor pe o perioadă este caracterizată de o scădere a atenuării egală cu
sau reducerea logaritmică a amortizării:
Coeficient de atenuare # 946; invers proporțional cu timpul # 964; în care amplitudinea oscilațiilor scade cu e ori:
Frecvența oscilațiilor amortizate este întotdeauna mai mică decât frecvența oscilațiilor naturale și poate fi găsită din expresie
unde Frecvența oscilațiilor naturale ale sistemului.
În consecință, perioada de oscilații amortizate este:
Cu o frecventa crescuta, perioada de oscilatie creste si cu perioada.
Pentru oscilații neamortizate nevoie efect variabil suplimentar al forței externe, care ar impinge punctul de material într-o direcție și apoi în cealaltă și a cărui funcționare se va face pentru a reduce în mod continuu de energie cheltuită în depășirea frecare. O astfel de forță variabilă se numește forța obligatorie. Oscilațiile neconfirmate care apar în cadrul acțiunii sale sunt forțate.
Dacă forța motrice se schimbă în conformitate cu expresia, atunci ecuația forțată de oscilație ia forma
unde Frecvența ciclică a forței motrice.
Aceasta este ecuația diferențială a oscilațiilor forțate. Soluția sa poate fi scrisă în formă
Ecuația descrie o oscilație armonică care are loc la o frecvență egală cu frecvența forței motrice, care diferă în fază de În ceea ce privește oscilația forței.
Amplitudinea oscilației forțate:
Diferența de fază dintre oscilațiile forței și a sistemului se găsește din expresie
Graficul grafic al oscilațiilor forțate este prezentat în figura 7.7.
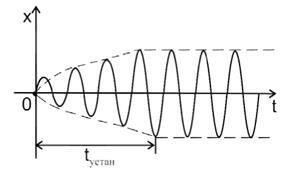
Figura 7.7 - Oscilații forțate
Pentru oscilații forțate, poate apărea un fenomen precum rezonanța. Rezonanța este o creștere accentuată a amplitudinii oscilațiilor sistemului.
Determinăm condiția în care se produce rezonanța, pentru aceasta luăm în considerare ecuația (7.30). Să găsim condiția în care amplitudinea presupune valoarea maximă.
Din matematică se știe că extremul unei funcții va fi atunci când derivatul este zero, adică
După transformare, ajungem
Prin urmare - frecvența de rezonanță.
În cel mai simplu caz, rezonanța apare atunci când forța periodică externă F variază în funcție de frecvență # 969; egală cu frecvența oscilațiilor naturale ale sistemului # 969; = # 969;
Procesul de propagare a oscilațiilor într-un mediu continuu, periodic în timp și spațiu, se numește proces de undă sau val.
Când se propagă valul, particulele mediului nu se mișcă cu valul, ci oscilează în apropierea pozițiilor lor de echilibru. Împreună cu valul de la particulă la particula mediului, numai starea mișcării vibraționale și energia sa sunt transmise. Prin urmare, proprietatea principală a valurilor, indiferent de natura lor, este transferul de energie fără transferul materiei.
Se disting următoarele tipuri de valuri:
Undele elastice (sau mecanice) se numesc tulburări mecanice care se propagă într-un mediu elastic. În orice val elastic există simultan două tipuri de mișcare: oscilația particulelor mediului și propagarea perturbării.
Un val în care vibrațiile particulelor din mediu și propagarea unei valuri apar într-o singură direcție se numește longitudinală. și un val în care particulele mediei oscilează perpendicular pe direcția de propagare a undelor se numesc transversale.
Undele longitudinale se pot propaga în medii în care forțele elastice apar sub compresiune și deformări de tensiune, adică corpuri solide, lichide și gazoase. Undele transversale se pot propaga într-un mediu în care forțele elastice apar în timpul deformării forfetare, adică în solide. Astfel, în lichide și gaze apar numai valuri longitudinale și în solide - atât longitudinal cât și transversal.
Un val elastic este numit sinusoidal (sau armonic) dacă vibrațiile corespunzătoare ale particulelor mediului sunt armonice.
Distanța dintre cele mai apropiate particule, oscilând în aceeași fază, se numește lungimea de undă # 955; .
Lungimea de undă este egală cu distanța la care se propagă valul într-un timp egal cu perioada de oscilații:
unde este viteza de propagare a valului.
Deoarece (unde # 957; frecvența oscilației)
Poziția geometrică a punctelor la care oscilațiile ajung la timpul t. se numește frontul valurilor. Locul geometric al punctelor oscilante în aceeași fază se numește suprafața undei.
Undele care rulează sunt valuri care transportă energie în spațiu. Pentru a deriva ecuația unui val de deplasare - dependența deplasării punctului oscilant pe coordonate și timp - luați în considerare un val sinusoidal plan care se propagă de-a lungul axei x.
Să presupunem că la un moment dat în mediul O există o sursă de oscilații:
La un anumit punct B. situat la o distanță x de la sursă,
oscilațiile se vor întârzia în timp din oscilațiile la punctul O. Deoarece timpul este necesar pentru distanța parcursă de undă x. unde este viteza de propagare a valului.
Ecuația de oscilații la punctul B va avea forma
De atunci
După înlocuire, ecuația unui val care se deplasează de-a lungul axei x:
În teoria valurilor se utilizează conceptul vectorului de undă:
Valoarea absolută a vectorului de undă este egală cu numărul de lungimi de undă pe segmentul 2π. Vectorul de undă este orientat în spațiu în direcția propagării undelor.
În cazul general, ecuația unei valuri care se propagă în spațiu de-a lungul axei x. are forma
unde este numărul de undă și viteza de fază sau viteza de propagare a undelor
Viteza de fază depinde de frecvență
Ecuația valurilor are în acest caz forma
Această ecuație este satisfăcută de valurile plane și sferice.
Articole similare
-
Prezentarea pe tema extracției de apă în autonomie forțată, a persoanelor cu autonomie forțată poate
Trimiteți-le prietenilor: