Definiția integratului dublu
Să avionul $ \ mathbf> $ fi mărginit închis regiune $ \ mathbf> $ cu porțiuni de frontieră netedă, și lăsați în câmp $ \ mathbf> $ defini funcția $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ .
Noi împărțim regiunea $ \ mathbf> $ arbitrar pe $ \ mathbf> $ subdomeniile $ \ mathbf> _ $, $ \ mathbf> _ $, $ \ mathbf> _ ,, \ mathbf> _ $ ,. Simbol $ \ mathbf> (\ mathbf> _) $ notam zona câmpului $ \ mathbf> _ $; Simbolul $ diam (\ mathbf>) $ și va continua să fie distanța maximă dintre două puncte aparținând câmpului $ \ mathbf> $: $$ diam (D) = \ mathop \ limits_ \ rho (P_1, P_2); $ $ prin simbolul $ d $ denotă cea mai mare dintre diametrele domeniilor $ \ mathbf> _ $:
Dacă există o limită a secvenței sumelor integrale pentru
$ D = \ mathop \ limits_ diam (D_i) \ la 0 $, nu depinde nici de metoda de împărțire a câmpului $ \ mathbf> $ pe un subdomeniu $ \ mathbf> _ $, nici alegerea punctelor $ \ mathbf> _ $, atunci funcția $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ este numit câmp integrabilă $ \ mathbf> $, dar valoarea acestei limite se numește dublu integralei funcției $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ în regiunea $ \ mathbf> $ și este notat cu $ \ iint \ limits_D $.Dacă vopsea valoarea $ \ mathbf> (\ mathbf>) $ prin coordonatele $ \ mathbf> $, și $ \ mathbf> $ ca $ \ mathbf> = \ mathbf> $, obține altă desemnare a unui dublu integrală: $ \ iint \ limits_D $. Deci, pe scurt,
Teorema existenței pentru integrala dublă
În cazul în care integrandul $ \ mathbf> (\ mathbf>, \ mathbf>) $ este continuă pe teren $ \ mathbf> $, atunci este integrabilă pe teren.
Semnificația geometrică a integrala dublă. Semnificația geometrică a fiecărui termen al sumei integrale
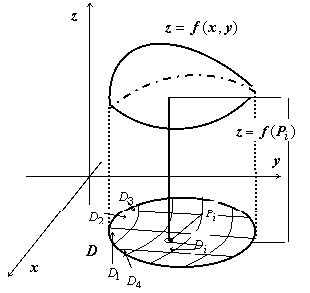
Din punct de vedere geometric, suma integrală este suma volumelor de cilindri cu bazele $ s (D _) $ și înălțimile $ f (P_i) $.
Dacă $ f (x, y) \ geqslant 0 $, atunci $ f (p_i) \ cdot s (D_i) $ - volumul unui cilindru drept cu o bază $ \ mathbf> _ $ înălțime $ \ mathbf> (\ mathbf> _) $ ; întreaga sumă integrală $ \ sum \ limits_ ^ n $ este suma volumelor unor astfel de butelii, adică volumul unui corp de pas - înălțimea pas, deasupra subdomeniu $ \ mathbf> _ $, egal cu $ \ mathbf> (\ mathbf> _) $. Când $ d = \ mathop \ limits_ diam (D_i) \ la 0 $, acest pas corpul se apropie de cea prezentată în corpul figurii, o zonă de fund limitat de $ \ mathbf> $, top - suprafață $ \ mathbf> = \ mathbf> ( \ mathbf> $, $ \ mathbf>) $, cu suprafața laterală cilindrică a ghidajului, care este limita de $ \ mathbf> $, paralel cu axa și generatoarele $ \ mathbf> $. Valoarea dublă integrală $ \ iint \ limits_D $ este egală cu volumul acestui corp.Citiți și:
Suprafață integrală a primului tip și proprietățile sale
Aplicațiile mecanice ale unui element curbilinar al primului tip
Definirea invariabilă a divergenței
Aplicații mecanice ale integrala triplă
Accesați cuprinsul $ \ Rightarrow \ Rightarrow \ Rightarrow $
Articole similare
Trimiteți-le prietenilor: