În geometrie, există multe probleme în care doriți să găsiți cea mai mare sau cea mai mică valoare a unei funcții. Ca o funcție, se poate lua în considerare perimetrul sau suprafața unei figuri sau, de exemplu, volumul unui corp, iar argumentul funcției este orice parametru al figurii sau corpului - lungimea laturii, unghiul dintre laturi și așa mai departe. După ce funcția este compilată, ea trebuie investigată cu ajutorul unui derivat pentru o valoare extremă. Trebuie avut în vedere că, de obicei, în astfel de exemple, funcția există pe un interval finit, determinat de geometria sistemului și de starea problemei.
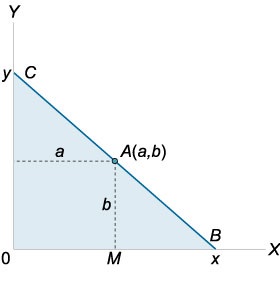
Pe planul de coordonate al primului trimestru stabilit punctul \ (A \ stânga (\ dreapta). \) Efectuați linie prin acest punct, o mică zonă de separare triunghi delimitată de această linie dreaptă și axele de coordonate (Figura \ (1 \)).
Luați în considerare triunghiurile \ (OBC \) și \ (MBA.) Aceste triunghiuri sunt similare. În consecință, relația \ [\ frac >> = \ frac >> \; \; \ textul \; \; \ frac = \ frac> \] unde coordonatele \ (x \) și \ (y \) satisfac \ (\ x \\) \ [y = \ frac >>.] Aria triunghiului va fi descrisă de următoarea funcție \ (S \ stânga (x \ dreapta): \) \ [.> = \ frac \ cdot \ frac >>> = >> \ dreapta) >>> \] calcula derivata: \ [>> \ dreapta) >>> \ dreapta) ^ \ prim = >> >>>> \ dreapta) ^ \ prim >> = \ cdot \ frac \ dreapta) - >> \ dreapta)> ^ 2 >>>> = \ cdot \ frac - 2ax - >> \ dreapta)> ^ 2 >>>> = \ dreapta) >> \ dreapta)> ^ 2 >>>.> \] funcția \ (S \ stânga (x \ dreapta) \) are puncte critice \ (x = 0, \) \ (x = a, \) \ (x = 2 \) deoarece \ (x> a, \) este punctul de decizie \ (x = 2a. \) Când se trece prin el modificările derivate de la semn min sa la plus, și anume \ (x = 2a \) este punctul minim al funcției \ (S \ left (x \ right). \)
Calculăm un alt cateter triunghi: \ [\ necesită y = \ frac >> = \ frac >> = \ frac> = 2b. \] Astfel, triunghiul cu cea mai mică zonă are picioare egale cu \ (2a \) și \ (2b. \)
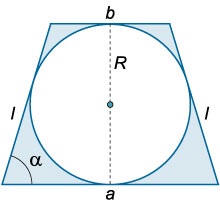
Trapezul isoscele este descris în jurul unui cerc de rază \ (R \) (Figura \ (2 \)). La ce unghi de la baza \ (\ alpha \) zona zonei umbrite va fi cea mai mica?
isoscel Zonă trapez este definit prin \ [= \ frac> \ cdot h \] unde \ (a, b \) - baza trapezului, \ (h \) - înălțimea. Evident, \ (. H = 2R \) Suprafața unui cerc este egal cu \ (= \ pi \.) Apoi zona regiunii umbrite este \ [- = \ frac> \ cdot 2R - \ pi> = \ dreapta) R - \ pi. > \] Deoarece trapezoidul este descris în jurul unui cerc, suma părților opuse ale acestuia este aceeași, adică \ [\; \ ;. >>>> = >>> \] Aici prin \ (\ ell \) denotă partea trapezului. Substituind \ (\ stânga (\ dreapta) \) în relația precedentă, obținem: \ [. >> \ cdot R - \ pi> = \ stânga (> - \ pi> \ dreapta)> \] Investigarea zonă \ (S \ stânga (\ alpha \ right) \) la o valoare extremă. Calculăm derivat \ (S „\ left (\ alpha \ dreapta): \) \ [\ left (> - \ pi> \ dreapta)> \ dreapta] ^ \ prim >> = \ stânga ( <- \frac^2>\ alpha >>> \ dreapta) \ cdot \ cos \ alpha> = <- \frac\cos \alpha>> ^ 2> \ alpha >>.> \] Este clar că derivatul este egal cu zero în condiția \ [cos \ alpha = 0, \; \; \ Rightarrow \ alpha = \ frac, \] iar atunci când treceți prin acest punct (cu creșterea \ (\ alpha \)) derivatul modifică semnul de la minus la plus. Prin urmare, \ (\ alpha = \ mare \ frac \ normalsize \) - punctul \ minim (S \ stânga (\ alpha \ dreapta) \.) În acest caz, trapez „degenerează„pătrat. Valoarea minimă a zonei cifrei este determinată de formula \ [> = \ left (\ right).]
Fereastra are forma unui dreptunghi delimitat de sus de un semicerc (Figura \ (3 \)). Perimetrul ferestrei este \ (P. \) Determinați raza semicercului \ (R, \) pentru care suprafața ferestrei este cea mai mare.
Evident, o parte a dreptunghiului este egal cu \ cealaltă parte este notat cu \ perimetrală a ferestrei este exprimată prin \ [P = \ pi R + 2R + 2y \.] De aici găsim \ (y: \) (2R \.) (Y \.) \ [y = \ frac \ left [\ right].] Zona ferestrei este: \ [>> + 2Ry> = >> + 2R \ cdot \ frac \ left [
\ right]> = >> PR - \ pi - 2> = >> - 2.> \] Expresia rezultată este o funcție a lui \ (S \ left \ R \ right). Găsim derivatul: \ [>> - 2> \ right] ^ \ prime >> =
=
\] Definiți punctele staționare: \ [\; \; \ right) R = 0,> \; \; >>> \] Deoarece al doilea derivat este negativ: \ [\ right] R> \ right] ^ \ prime >> = <- \left( \right) r\)). Из данного бревна требуется вырезать балку в форме параллелепипеда с квадратным сечением наибольшего объема.
Presupunem că axele jurnalului și grinzilor coincid. Trunchiul de con și înscrisă într-un paralelepipedului sunt prezentate schematic în secțiune în figura \ (14 \) este definită de un volum \ paralelipiped [V = y, \] unde \ (\ x) - la partea de jos a unui paralelipiped pătrat, și \ (y \) - înălțimea sa.
Trimiteți-le prietenilor: