Teorema lui Vieta. Exemple de soluții
În această prelegere vom cunoaște relațiile curioase dintre rădăcinile ecuației patrate și coeficienții ei. Aceste relații au fost descoperite pentru prima oară de matematicianul francez Francois Viet (1540-1603).

De exemplu, pentru ecuația 3x2 - 8x - 6 = 0, fără a găsi rădăcinile ei, putem folosi imediat teorema lui Vieta pentru a spune că suma rădăcinilor este egală cu. și produsul rădăcinilor este
adică - 2. Și pentru ecuația x 2 - 6x + 8 = 0 concluzionăm: suma rădăcinilor este de 6, produsul rădăcinilor este egal cu 8; Apropo, aici nu este greu să ghicești care sunt rădăcinile: 4 și 2.
Dovada teoremei lui Vieta. Rădăcinile x1 și x2 ale ecuației patratice ax 2 + bx + c = 0 se găsesc prin formule
unde D = b 2 - 4 ac este discriminantul ecuației. Combinând aceste rădăcini,
avem
Acum calculăm produsul rădăcinilor x1 și x2. Avem
A doua relație este dovedită:
Notă. Teorema Wyeth deține în cazul în care ecuația de gradul doi are o radacina (t. E. Când D = 0), este simplu în acest caz, se consideră că ecuația are două rădăcină identică, la care se aplică raportul menționat mai sus.
O formă deosebit de simplă este relația dovedită pentru ecuația cuadratoare redusă x 2 + px + q = 0. În acest caz primim:
x1 = x2 = -p, x1 x2 = q
și anume suma rădăcinilor ecuației cuadratoare reduse este egală cu al doilea coeficient luată cu semnul opus, iar produsul rădăcinilor este egal cu termenul liber.
Folosind teorema Vieta, este posibil să se obțină și alte relații între rădăcini și coeficienții ecuației patratice. Fie, de exemplu, x1 și x2 să fie rădăcinile ecuației cvadrate reduse x 2 + px + q = 0. Atunci
Cu toate acestea, scopul principal al teoremei lui Viet nu este acela că exprimă unele relații între rădăcini și coeficienții ecuației patratice. Mai important, cu ajutorul teoremei lui Viet derivăm formula de expansiune a unui trinomial cuadrat în multiplicatori, fără de care nu vom face fără.
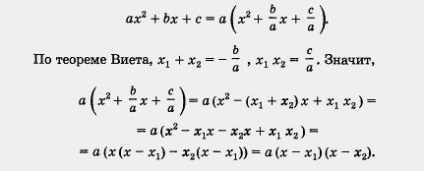
Exemplul 1. Factorul trinomial pătrat 3x 2 - 10x + 3.
Soluția. Rezolvând ecuația 3x 2 - 10x + 3 = 0, găsim rădăcinile trinomului triunghiular 3x2 - 10x + 3: x1 = 3, x2 =.
Folosind Teorema 2, obținem
Există un sens în loc să scrieți 3x - 1. Apoi, obțineți în cele din urmă 3x 2 - 10x + 3 = (x - 3) (3x - 1).
Rețineți că un trinomial quadratic dat poate fi factorizat și fără a aplica Teorema 2, folosind metoda de grupare:
3x2 - 10x + 3 = 3x2 - 9x - x + 3 =
= 3x (x - 3) - (x - 3) = (x - 3) (3x - 1).
Dar, după cum puteți vedea, prin această metodă succesul depinde de faptul dacă reușim să găsim o grupare de succes sau nu, în timp ce în primul rând succesul este garantat.
Exemplul 1. Reduceți fracția
Soluția. Din ecuația 2x2 + 5x + 2 = 0 găsim x1 = -2,
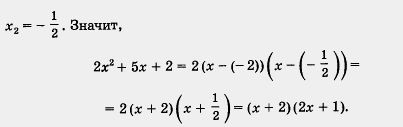
Din ecuația x2 - 4x - 12 = 0 găsim x1 = 6, x2 = -2. prin urmare
x 2 - 4x - 12 = (x - 6) (x + 2)) = (x - 6) (x + 2).
Și acum reducem fracțiunea dată:
Exemplu 3. Extindeți expresiile:
a) x4 + 5x2 + 6; b) 2x + 3
R e w n e. A) introduce noua variabila y = x 2. Aceasta permite rescrierea expresiei predeterminate ca polinom pătratic în variabila y, și anume în forma y 2 + bu + 6.
Rezolvând ecuația pentru 2 + până la + 6 = 0, găsim rădăcinile trinomului pătrat y 2 + 5y + 6: y1 = -2, y2 = -3. Acum folosim Teorema 2; avem
y + 5y + 6 = (y + 2) (y + 3).
Trebuie să ne amintim că y = x 2. adică să ne întoarcem la expresia dată. Și așa,
x 4 + 5 x 2 + 6 = (x 2 + 2) (x 2 + 3).
b) Introducem o nouă variabilă y =. Aceasta ne permite să rescriem expresia dată sub forma unui trinomial quadratic în raport cu variabila y, și anume în forma 2y 2 + y - 3. Ecuația de rezolvare
2y 2 + y - 3 = 0, găsim rădăcinile trinomului cuadrat 2y 2 + y - 3:
y1 = 1, y2 =. Mai departe, folosind Teorema 2, obținem:
Trebuie să ne amintim că y =. adică să se întoarcă la expresia dată. Și așa,
În încheierea acestei secțiuni, unele argumente, legate din nou de teorema lui Viet sau, mai exact, de afirmația inversă:
dacă numerele x1. x2 sunt astfel încât x1 + x2 = -p, x1 x2 = q, atunci aceste numere sunt rădăcinile ecuației
Cu ajutorul acestei afirmații, multe ecuații pătrate pot fi rezolvate verbal, fără a folosi formule rădăcinoase greoaie și, de asemenea, pentru a forma ecuații pătrate cu rădăcini date. Să dăm câteva exemple.
2) x 2 + 11x + 30 = 0. Aici x1 + x2 = -11, x1 x2 = 30. Nu este greu de ghicit că x1 = -5, x2 = -6.
Notă: dacă termenul liber al ecuației este un număr pozitiv, atunci ambele rădăcini sunt fie pozitive, fie negative; acest lucru este important de luat în considerare la selectarea rădăcinilor.
3) x 2 + x - 12 = 0. Aici x1 + x2 = -1, x1 x2 = -12. Este ușor de ghicit că x1 = 3, x2 = -4.
Notă: dacă termenul liber al ecuației este un număr negativ, atunci rădăcinile sunt diferite în semn; acest lucru este important de luat în considerare la selectarea rădăcinilor.
4) 5x 2 + 17x - 22 = 0. Este ușor de observat că x = 1 satisface ecuația, adică x1 = 1 este rădăcina ecuației. Deoarece x1 x2 = -. și x1 = 1, atunci obținem că x2 = -.
5) x 2 - 293x + 2830 = 0. Aici x1 + x2 = 293, x1, x2 = 2830. Dacă ne acorde atenție faptului că 2830 = 283 • 10 si 293 = 283 + 10, devine clar faptul că x1 = 283, x2 = 10 (și acum imaginați ce calcule ar trebui să fie efectuate pentru a rezolva această ecuație patratică folosind formule standard).
6) formează ecuația de gradul doi, astfel încât rădăcinile erau numere x1 = 8, x2 = - 4. De obicei, în astfel de cazuri, face redusă ecuația pătratică x 2 + p + q = 0.
Avem x1 + x2 = -p, prin urmare, 8 = 4 = -p, adică p = -4. Mai mult, x1 x2 = q, adică 8 «(- 4) = q, de unde obținem q = -32. Deci, p = -4, q = -32, atunci ecuația patratică necesară are forma x 2 -4x-32 = 0.
Trimiteți-le prietenilor: