Să existe o ecuație caracteristică a unui sistem închis
Pentru a determina ordinea în care intervalul poate varia parametrii a1 ... o operațiune sub stabilă a sistemului, a fost dezvoltat și rafinat (1940 AA Sokolov 1948 NEIMARK) metoda pentru zonele de durabilitate izolare.
Să fie un grafic al timpului de călătorie al lui Mihailov pe limita de stabilitate. Dacă sistemul este la limita de stabilitate, atunci complot polar Mikhailova D (jv) trece prin origine, care poate fi afișată prin ecuația:
În ecuația (6.45), selectăm parametrii necesari și tragem o limită pentru v = 0¸¥. Această limită se numește partiția D și reprezintă maparea limitei de stabilitate în planul rădăcinilor în planul parametrilor sistemului.
Figura 6.26 D-partiționare
Pentru ca sistemul să fie stabil, este necesar ca toate rădăcinile ecuației caracteristice a unui sistem închis să fie "lăsate".
Coeficienții ecuației caracteristice depind de constantele de timp
Pentru a determina natura efectului parametrilor asupra stabilității, transferați limita de stabilitate de la planul rădăcinilor la planul parametrilor. Aceasta se face din condiția D3 (jv) = 0. În această ecuație, parametrii sunt extrași și o limită de stabilitate (curba de descompunere D) este construită în planul parametrilor.
stabilitatea frontierei standuri umbrită de regula Neumark. Cand conduceti de-a lungul axei imaginare de la w = - ¥ la w = + ¥ stânga eclozat, lăsând zona rădăcinilor cu o parte negativă reală stânga.
Avem: - ecuația caracteristică a unui sistem închis. Este necesar să se găsească ecuația limită de stabilitate, adică la - ¥ D-partiție pentru un parametru complex. 1) Înregistram. și anume Din polinomul D (p), luați parametrul K. și S (p) este un polinom care nu conține parametrul K. 2) În continuare - împărțim în părțile reale și imaginare. 3) Construiește dependența K (v). dat de diferite valori ale v. Obținem limita regiunilor de stabilitate. 4) Am identificat regiunile de stabilitate prin ecloziune conform Neimark, pentru aceasta: a) notați direcția mișcării v de la - ¥ k + ¥; b) umbrați partea stângă a curbei în raport cu mișcarea. Întregul plan este împărțit în trei zone (I, II și III) (Figura 6.27). O parte din planul în care latura îndreptată accident vascular cerebral (zona I) afișează stânga semiplanul din rădăcini, și, prin urmare, are cel mai mare număr de rădăcini și din stânga este o zonă mai mare stabilitate.
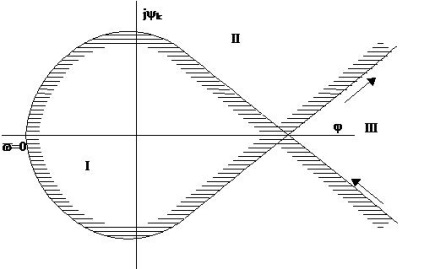
Figura 6.27 Limita regiunilor de stabilitate.
Trecerea de la zona I la zona II, adică curba D-trecere partiție a porțiunii umbrită nu hașurat în pierdut unul negativ și unul rădăcină pozitivă este dobândită (se mută rădăcină la dreapta semiplanul).
Stabilitatea este redusă în zona III, unde se pierd două rădăcini negative.
Deci, regiunea I (Figura 6.27) are cea mai mare marjă de stabilitate. Verificăm stabilitatea la punctul 0. Deoarece parametrul K este real, găsim acele valori ale lui K. care sunt în regiunea I pe axa reală. Cu aceste valori, ATS va avea cea mai mare marjă de stabilitate.
Un exemplu. Ecuația caracteristică a unui sistem închis:
Să găsim valoarea lui K corespunzătoare celei mai mari stabilități.
4) deoarece parametrul k este real, valorile reale ale k = j (v) și așezate pe segmentul AB, adică de la -1 la 19,8 corespund funcționării stabile a ATS.
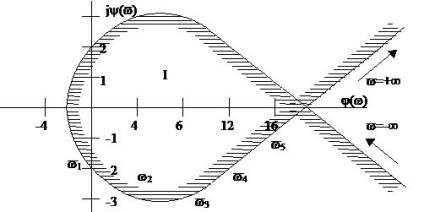
Figura 6.28 De exemplu, determinarea celei mai mari stabilități a unui sistem închis
De multe ori, zone cu diferite domenii de stabilitate este mai mic decât gradul de ecuația caracteristică, și, prin urmare, numărul de rădăcini ale ecuației caracteristice. În acest caz, stabilitatea regiunii mai oferă doar o stabilitate, dar nu răspunde la întrebarea dacă sistemul este stabil atunci când este necesar, după alegerea parametrilor pentru a examina stabilitatea altor metode.
Cel mai adesea, acest lucru se face cu valoarea parametrului egal cu zero, adică la originea curbei descompunerii D.
În ecuația noastră caracteristică am stabilit k = 0.
și găsim rădăcinile care egalează la zero toți factorii
și anume Zona I corespunde funcționării stabile a sistemului de control automat cu o schimbare în k de la -1 la 19,8, adică de la 0 la 19,8.
Pentru a determina numărul absolut de rădăcini negative pentru o anumită valoare a parametrului studiat, trebuie să rezolvăm ecuația caracteristică și să găsim numărul de rădăcini care ne interesează. De obicei, valoarea parametrului este luată egală cu zero (originea coordonatelor planului parametru). Ecuația caracteristică este simplificată. În cele ce urmează, determinăm numărul de rădăcini în toate zonele prin eclozarea curbei descompunerii D.
Selectăm regiunea cu cea mai mare stabilitate și comparăm numărul de rădăcini negative cu exponentul n al ecuației caracteristice. Dacă numărul rădăcinilor negative este n, atunci sistemul este stabil.
Articole similare
Trimiteți-le prietenilor: