§ 6. Comparația seturilor. Seturi de calculatoare. 62
6.1. Conceptul de cardinalitate a setului 62
6.2. Seturi de calculatoare 64
6.3. Neconcordabilitatea setului 67
Conceptul de cardinalitate
Fondatorul doctrinei seturilor este matematicianul german Georg Kantor (G. Kantor, 1845-1918), profesor de la Halle. Una dintre marile merite ale lui Cantor este aceea că a stabilit conceptele exacte care apar în problema împărțirii seturilor infinite în mărime sau în volum. Această problemă este trivială pentru seturile finite și este rezolvată prin compararea numărului de elemente din ele. Dar pentru seturi infinite, problema comparării lor conduce la o problemă dificilă: poate un număr infinit de elemente dintr-un set să fie considerat mare, egal sau mai mic decât un număr infinit de elemente dintr-un alt set? După sugestia lui Cantor, o comparație a două seturi se realizează printr-o corespondență unu-la-unu între elementele lor.
Se spune că între elementele a două seturi

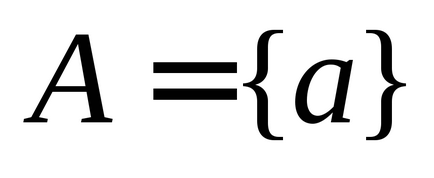
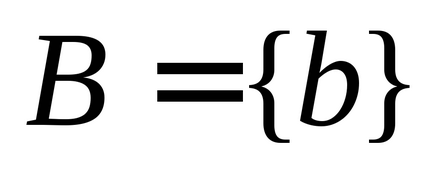
1) fiecare element
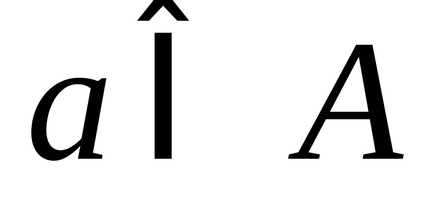
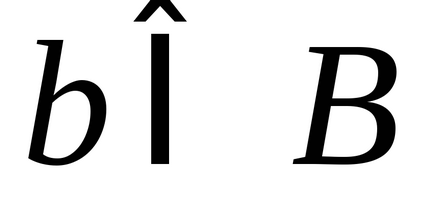
2) fiecare element
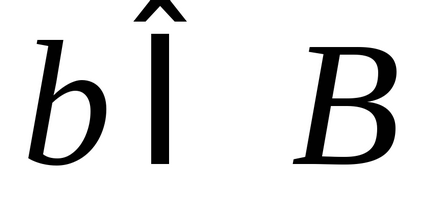
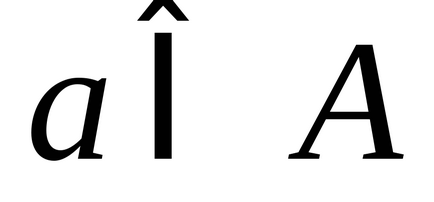
Definiția seturilor echivalente (echipollente)
Două seturi, între elementele din care se poate stabili o corespondență unu-la-unu (bijecție), se numesc seturi echipollente. sau seturi de aceeași putere. sau seturi de putere echivalente.
Desemnarea seturilor echivalente (echipotent):
Astfel, există întotdeauna o mapare bijectivă între elementele seturilor echivalente (echivalente). Dacă o astfel de cartografiere nu poate fi stabilită, seturile au puteri diferite. se pare că indiferent de modul în care încercăm să potrivim elementele celor două seturi, vor rămâne mereu elemente inutile și întotdeauna din același set, care are prin urmare "putere mai mare". De exemplu, este evident că două seturi finite sunt echivalente dacă și numai dacă ele conțin același număr de elemente.
Exemplu (seturi echivalente finite)
unde
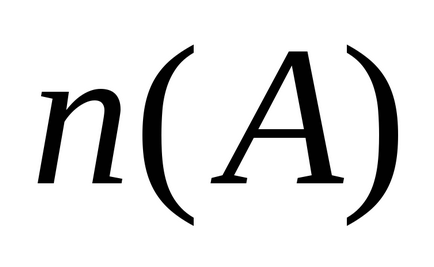
și
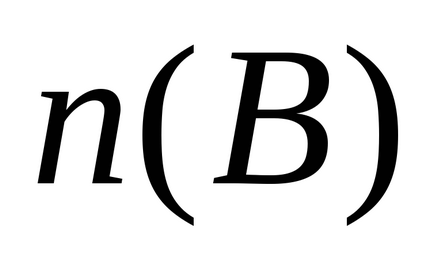

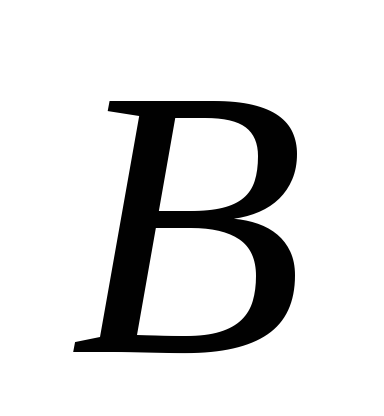
Un set care nu este finit se numește infinit și numărul elementelor din el nu poate fi exprimat prin nici un număr. Prin urmare, este posibilă compararea seturilor infinite numai prin puterea lor, adică folosind o procedură care stabilește o corespondență unu-la-unu între elementele acestor seturi.
De asemenea, este clar că:
1) a două seturi finite

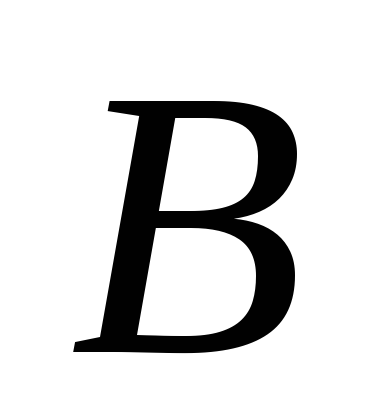
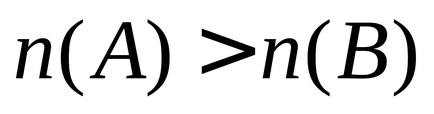

2) fiecare set finit


Exemple (seturi infinite echivalente)
adică mulțimea N a tuturor numerelor naturale are aceeași caracteristică ca și cea proprie, care constă doar în numere egale.
2) adică setul


seturi

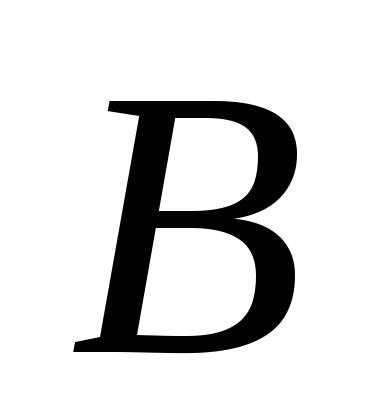
)
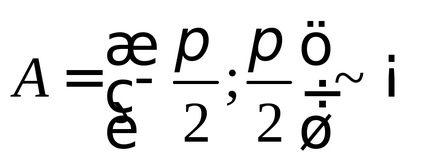
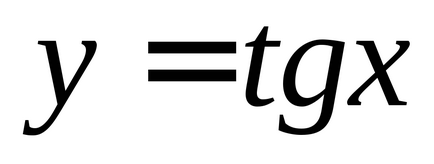
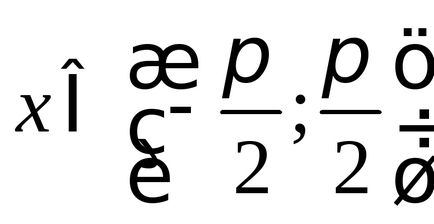
(Figura 2), deci setul
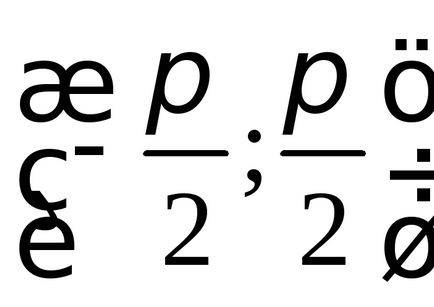
Aceste exemple arată în mod clar că partea privată a (subsetul propriu-zis) a unui set infinit poate avea o putere egală cu el, adică, pentru un set infinit nu este o afirmație adevărată „parte este mai mică decât întregul.“
Articole similare
Trimiteți-le prietenilor: