Proprietatea principală a planului proiectiv este "simetria" rolurilor jucate de puncte și linii în definiții și teoreme, iar dualitatea este formalizarea acestui concept. Există două abordări ale acestei dualități: una care folosește limba (vezi "principiul dualității" de mai jos) și o altă abordare mai funcțională. Ele sunt complet echivalente și ambele servesc ca punct de plecare pentru versiunile axiomatice ale geometriei. În abordarea funcțională există o corespondență între geometrii, care se numește dualitate. În exemple particulare, o astfel de corespondență poate fi construită în mai multe moduri. Conceptul de dualitate al unui avion se extinde ușor la dualitate în orice geometrie proiectivă dimensională finită.
Principiul dualității [ ]
Dacă definim ca un plan proiectiv a structurii axiomatic incidență în ceea ce privește un set de puncte P. set de linii L și o incidență relație binară I. determină ce puncte se află pe liniile drepte care, este posibil să se definească o structură de plan duală.
Dacă schimbați rolurile de "puncte" și "linii" în structura incidenței
obținem o structură dublă
unde I * este relația inversă [la] I. C * este de asemenea un plan proiectiv, care se numește planul dual (dual) pentru C.
Dacă C și C * sunt izomorfe, atunci C se numește auto-dublă. Proiectiv plane PG (2, K) pentru fiecare domeniu (sau, mai general, pentru orice divizare inel izomorfă dubla sale) K sunt auto-duale. În special, perturbările unui plan de ordine finită sunt întotdeauna auto-duale. Cu toate acestea, printre avioane non-Desarguesian există ca (de exemplu, planul Hughes [en]) auto-duală, nu a auto-duală (de exemplu, Hall-plan).
Pentru declarația plan proiectiv privind punctele, avioane și incidența lor obținute de la un alt astfel de aprobare prin schimbul de termeni „punct“ și „linia“ (schimbarea, dacă este necesar, gramatica) se numește declarația dublă. Declarație dublă pentru „Două puncte trece printr-o linie unic“ va fi „Două linii se intersectează la un moment dat.“ Formarea afirmației duale se numește dualizare a afirmației.
Dacă afirmația este adevărată în planul proiectiv C, atunci afirmația duală trebuie să fie adevărată în planul dual C *. Acest lucru rezultă din faptul că dualizarea fiecărei instrucțiuni în dovada "în C" dă o declarație în dovada "în C *".
Principiul dualității unui plan spune că dublarea oricărei teoreme în planul pro-planic auto-dual C generează o altă teorie adevărată în C.
Acest concept poate fi generalizat în dualitatea spațiului tridimensional, unde conceptele de "puncte" și "planuri" schimbă rolurile (iar liniile rămân drepte). [1] Aceasta duce la principiul dualității spațiului. Sunt posibile generalizări suplimentare (a se vedea mai jos).
Aceste principii oferă un motiv bun pentru utilizarea termenului "simetric" pentru relația de incidență. Deci, în schimb oferă „punct se află pe linia“ puteți spune „punct și incidentul direct“, precum și pentru aprobarea dualizarea suficiente cuvinte punct și linie pentru a interschimba ( „linia dreaptă și un incident punct“).
Prin definiție, un plan proiectiv este un set de puncte și linii, iar o transformare proiectivă poate cartografia punctele spre puncte și linii drepte către linii drepte. O astfel de transformare se numește colinăție. [2] Atunci când se analizează dualitatea unui plan proiectiv, este luată în considerare o altă cartografiere, în care punctele sunt transformate în linii drepte și linii drepte în puncte. O astfel de mapare se numește o corelație. [3] Maparea proiectivă este definită de cerințele de conservare
1) incidența punctelor și liniilor 2) a raportului dublu [4]
Teoreme duale [ ]
Deoarece planul real proiectiv PG (2, R) este auto-dual, există o serie de afirmații binecunoscute duale între ele. Printre acestea:
Dualitatea ca o cartografiere [ ]
Dualitate (plane) - o cartografiere a planului proiectiv C = (P, L, I), în dubla sa C * = (L, P, I *), păstrând proprietatea incidență. Astfel, dualitate (planul) sigma reprezintă un punct în direct și direct la punctele (P σ = L și σ = P L), în așa fel încât, dacă Q se află pe linia m (notat QI m), atunci Q σ I * m σ ⇔ m σ IQ σ. Dualitatea (planul), care este un izomorfism, se numește o corelație. [5] Existența unei corelații înseamnă auto-dualitatea planului proiectiv.
În cazul special când planul proiectiv este de tip PG (2, K), unde K este un inel de diviziune, dualitatea se numește transformare reciprocă. [6] Prin teorema fundamentală a geometriei proiective, transformarea reciprocă este compoziția unei funcții automorfe pe K și a unei transformări proiective. Dacă automorfismul utilizat este identic, transformarea reciprocă se numește corelație proiectivă.
Corelarea ordinii a doua (involuția) se numește polaritate. Dacă corelația nu este o polaritate, atunci φ 2 este o colinăție netrivială.
Acest concept de mapare poate fi extins la spații de dimensiuni mai mari, astfel încât referința la plan poate fi îndepărtată.
Dualitate de dimensiuni mari [ ]
Dualitatea planului proiectiv este un caz special de dualitate pentru spațiile proiective. Conversii PG (n, K) (care sunt notate ca KP n), unde K - câmp, schimbul de dimensiuni r obiecte cu obiecte de dimensiune n - 1 - r (= r codimensional + 1). Astfel, într-un spațiu proiectiv de dimensiune n a punctului (dimensiunea 0) va corespunde hiperplane (codimensional 1), liniile care trec prin două puncte (dimensiune 1) va corespunde intersecția a două hiperplane (codimensional 2), și așa mai departe.
Punct de PG (n, K) poate fi considerată ca o nenulă vector în spațiul vectorial (n + 1) dimensional peste K. în care identificăm cei doi vectori, în cazul în care acestea diferă numai printr-o multiplicare scalar. O altă modalitate de a reprezenta ambele puncte ale unui spațiu proiectiv n-dimensional este ca liniile care trec prin originea în Kn + 1. Acestea sunt subspații vectoriale 1-dimensionale. Astfel, n vector -dimensional câmpurile subspațiali Kn + 1 sunt (n - 1) hiperplan -dimensional geometric proiectiv n spații peste K.
Un vector nenulos u = (u0, u1, un) în Kn + 1 definește un subspațiu geometric (hiperplane) dimensional (n - 1) Hu,
Vectorul u. folosit pentru a defini hyperplane, vom denota prin uH. și pentru a indica punctul corespunzător capătului vectorului, folosim notația uP. În ceea ce privește produsul scalar obișnuit. Hu = xP: uH • xP = 0>. Deoarece K este un câmp, produsul scalar este simetric, ceea ce înseamnă că uH • xP = u0 x0 + u1 x1 +. + un xn = x0 u0 + x1 u1 +. + xn un = xH • uP. Se poate defini o transformare reciprocă uP ↔ Hu între puncte și hiperplane. Această corespondență poate fi extinsă la linii drepte formate din două puncte și la intersecția a două hiperplane și așa mai departe.
Pe plan proiectiv PG (2, K) cu un câmp K avem potrivire: coordonate omogene (a, b, c) ↔ linii, dată de ecuațiile ax + de + cz = 0. PG spațiu proiectiv (3, K) de potrivire arată punct în coordonate omogene (a, b, c, d) ↔ planul dat de ecuații ax + de + cz + dw = 0. Această corespondență prezintă, de asemenea, linia dreaptă definită prin două puncte (a1, b1, c1, d1) și (a2, b2, c2, d2), o linie dreaptă care este intersecția a două plane definite de ecuațiile a1 x + b1 y + c1 z + d1 w = 0 și a2 x + y + b2 + c2 z d2 w = 0.
Spațiu tridimensional [ ]
În hărțile polare ale unui spațiu proiectiv real 3-dimensional PG (3, R), punctele corespund planurilor, iar liniile corespund liniilor. În stereometrie, există o dualitate de polyhedra. atunci când punctele sunt duale față de fețe, iar marginile sunt duale la margini, astfel încât icosaedrul este dublu la un dodecaedru. iar cubul este dublu la un octaedru.
Construcția geometrică a transformării reciproce [ ]
Valoarea în PG (2, R) în coordonate omogene pot fi descrise geometric. În acest scop, modelul real planului proiectiv [en] „Unitate sferă cu antipozi identificare [7],“ sau, echivalent, liniile de modele și avioane care trec prin originea coordonatelor spațiului R 3. asociat cu linia care trece prin origine, ortogonal pe planul tălpii, care conține originea. În cazul în care acest model este considerat puncte drepte și un plan - dreapta PG plan proiectiv (2, R), această comparație devine corespondență (și de fapt - cartografierea polar) a planului proiectiv. Modelul sferic poate fi obținut ca intersecția liniilor și planuri care trec prin origine cu sfera unitate având un centru la origine. Direct intersectează sfera în două puncte opuse, care sunt identificate pentru a obține un punct al planului proiective, planul domeniului de aplicare transversală a cercurilor mari. care sunt liniile planului proiectiv.
Faptul că o astfel de comparație "păstrează" incidența este ușor de arătat pe modelul de linii drepte și planuri. Punctul care intră într-o linie dreaptă în planul proiectiv corespunde unei linii drepte situate pe planul din model. Conform comparației, planul devine o linie dreaptă care trece prin origine și perpendiculară pe plan. Această imagine (linie dreaptă) este perpendiculară pe orice linie dreaptă situată în plan și în special la linia dreaptă originală (punctele planului proiectiv). Toate liniile drepte perpendiculare pe linia inițială formează un plan care este planul asociat al liniei originale. Astfel, imaginea liniei stă în imaginea planului, astfel încât incidența să fie păstrată.
Polonezi și polari [ ]
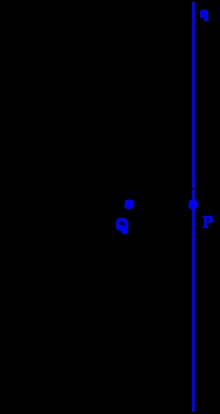
Polul și polarul pentru cercul O. P = Q '. q este un polar pentru Q. Q este un pol pentru q.
În spațiul euclidian, fixăm un cerc C cu centrul O și o rază r. Pentru fiecare punct P. diferit de O, definim imaginea lui Q '. astfel încât OP • OQ = r 2. Cartografia P → Q se numește inversiunea [en] [8] în raport cu cercul C. Linia dreaptă q. Trecând prin P. perpendicular la OP. se numește polar al punctului Q în raport cu cercul C.
Fie q o linie care nu trece prin O. Lăsăm perpendicularul de la O la q. care intersectează q la punctul P (acesta este punctul liniei q mai apropiat de O). Imaginea punctului Q (punctul P) sub inversiune relativ la C se numește polul liniei q. Dacă punctul M se află pe linia q (care nu trece prin O), atunci polul liniei drepte q se află pe polarul punctului M și invers. Un proces care păstrează incidența, în care punctele și liniile intră în polar și pol, în raport cu C, se numește transformare proiectivă. [9]
Pentru a face acest proces de transformare reciprocă spațiu (plan non-proiectiv) euclidiene trebuie să se extindă la planul Euclidian extins prin adăugarea de linie la infinit [en] și puncte la infinit [en]. care se află pe această linie infinit de îndepărtată. Acest plan extins, definim punctul polar O ca o linie la infinit (și O este un pol la infinit), iar polii liniilor drepte care trec prin O la punct infinit, în care, în cazul în care linia are o pantă s (≠ 0), polul este un punct infinit de îndepărtat corespunzător clasei de linii paralele cu panta -1 / s. Polul pentru axa x - acesta este punctul de la infinit de linii verticale și axa y pol - punctul de la infinit de linii orizontale.
Construcția transformării polare pentru inversiunea relativă la cercul dat mai sus poate fi generalizată folosind inversarea în raport cu secțiunile conice (pe planul real extinse). Transformarea reciprocă construită în acest fel este o corelație proiectivă a ordinii a doua, adică transformarea polară.
Cartografierea sferei în plan [ ]
Modelul unui plan proiectiv cu sfera unității este izomorf (ținând cont de proprietatea de incidență) a modelului plan, unde planul este extins de linia proiectivă la infinit. În acest model, punctele opuse ale sferei (față de centru) sunt considerate a fi un punct.
Pentru a compara punctele unei sfere pe un plan, presupunem că sfera este tangentă la plan într-un anumit punct și alegem acest punct ca fiind originea planului. Acum trageți o linie prin punctul din sferă și centrul sferei. Această linie dreaptă va traversa sfera la un moment dat. Punctul rezultat poate fi folosit pentru a construi o cartografiere unu-la-unu
Liniile drepte pe un model plan sunt proiecții ale cercurilor mari ale unei sfere, deoarece un plan poate fi tras printr-o linie dreaptă în plan și originea coordonatelor tridimensionale, iar acest plan va intersecta sfera de-a lungul unui cerc mare.
După cum se poate observa, orice cerc mare pe sferă poate fi asociat cu un punct proiector corespunzător unei singure linii drepte perpendiculare pe planul pe care se află cercul și care poate fi definit drept dublu. Această linie dreaptă traversează planul tangent și aceasta arată cum să asociem un singur punct al planului oricărei linii în acest plan, astfel încât punctul să fie dublu față de linie.
Notă [ ]
Proprietăți [ ]
Referințe [ ]
Legături externe [ ]
Trimiteți-le prietenilor: