Rezolvarea ultimei ecuații pentru



Considerăm câteva exemple, în fiecare dintre acestea realizându-ne o secvență de acțiuni pentru rezolvarea problemei de identificare a valorilor proprii și vectorilor proprii ai matricei.
Găsiți valorile proprii și vectorii proprii ai matricei
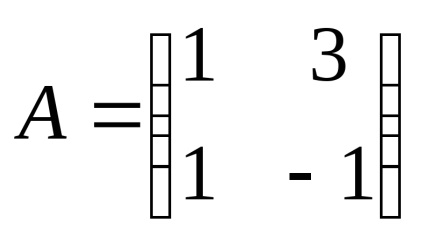
Matricea are dimensiunea 2

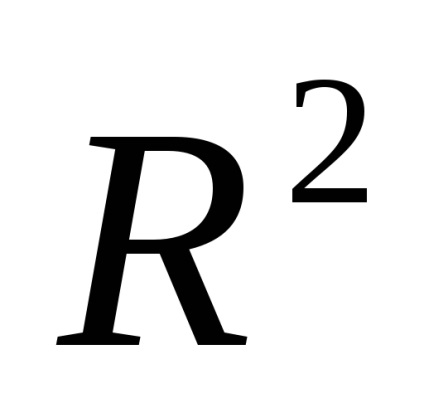
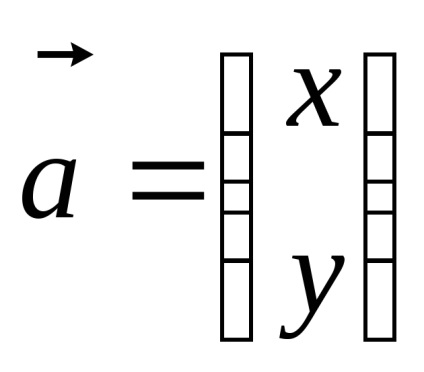
Formăm ecuația pentru găsirea vectorilor proprii sub formă de matrice:
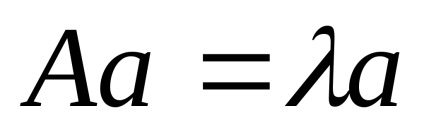

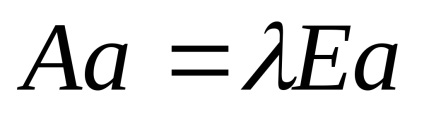

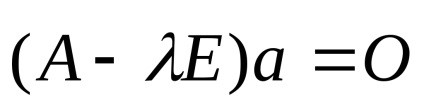
3. Rescriem ecuația matricei sub forma unui sistem de ecuații:
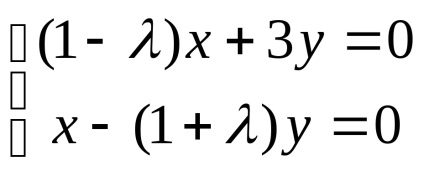
Un sistem omogen are soluții nonzero dacă și numai dacă determinantul matricei sale principale este 0. Obținem ecuația caracteristică a sistemului și îl rezolvăm:
.
Valorile proprii ale matricei

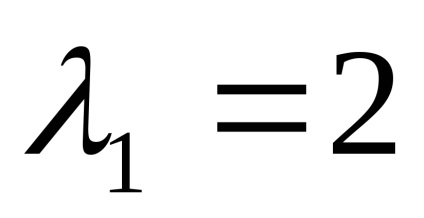
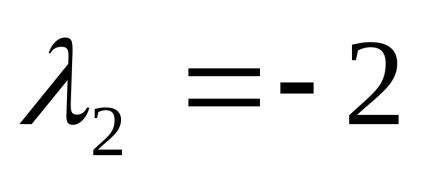
Să găsim vectorii proprii pentru fiecare valoare proprie:
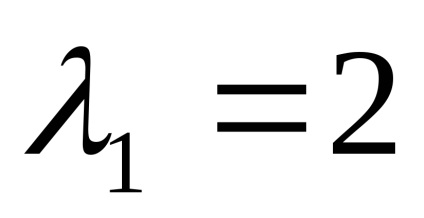
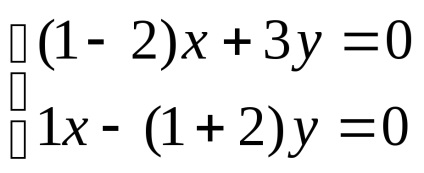
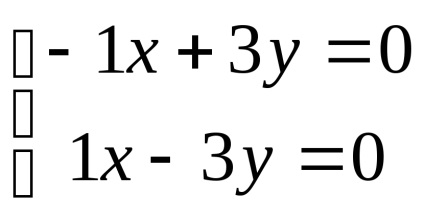
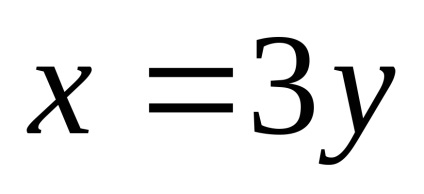
lăsa
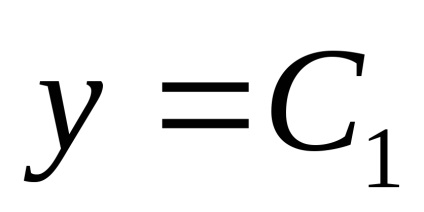

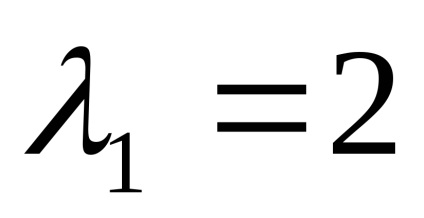
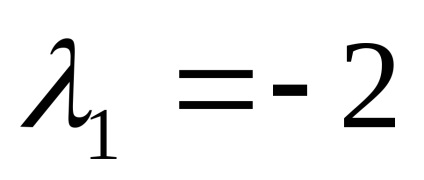
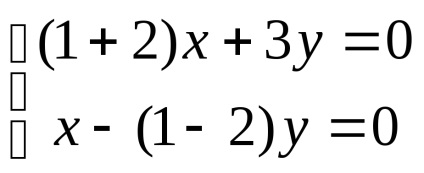
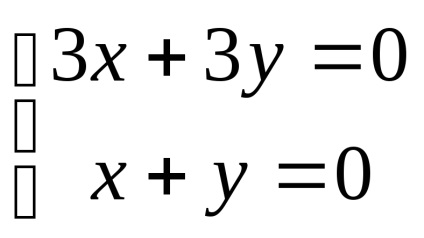
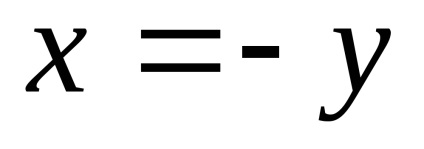
lăsa
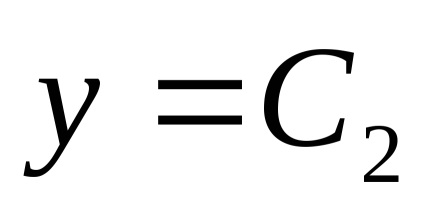

, corespunzătoare valorii proprii
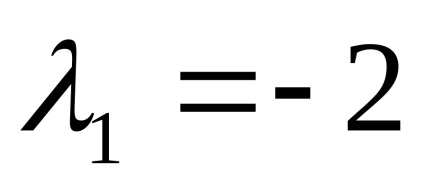
Exemplul 2. Găsiți valorile proprii și vectorii proprii ai unui operator liniar. dat într-o anumită bază de matricea A =
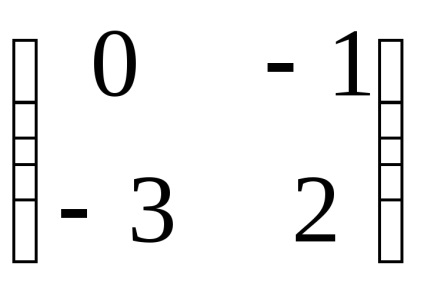
Formăm și rezolvăm ecuația caracteristică
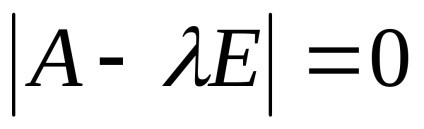
Apoi ecuația caracteristică ia forma:
,
,
- valorile proprii ale unui operator liniar.
Să găsim vectorii proprii care corespund valorii proprii
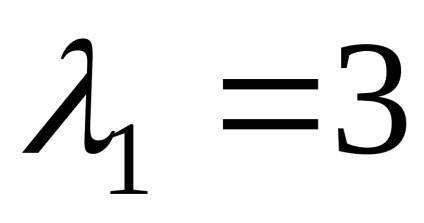
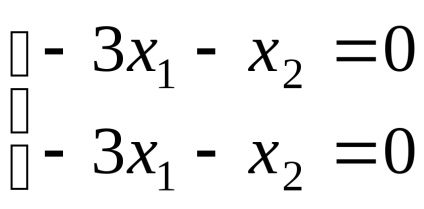
Presupunând în ultima egalitate
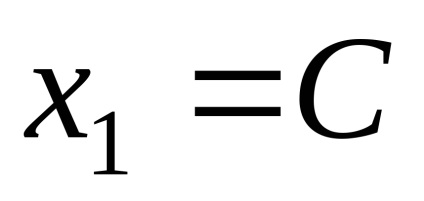
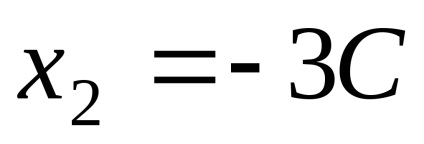
De unde vectorii proprii corespund valorii proprii
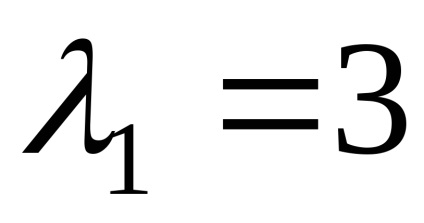
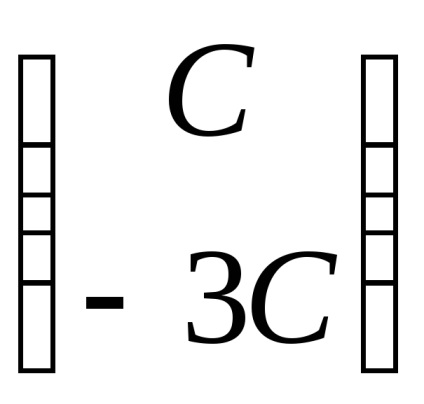
Să găsim vectorii proprii care corespund valorii proprii
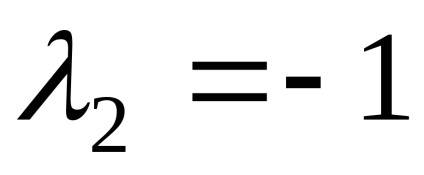
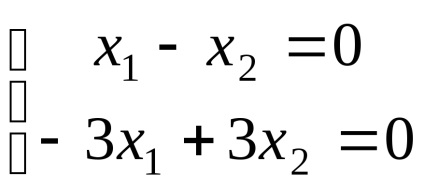
Presupunând în ultima egalitate
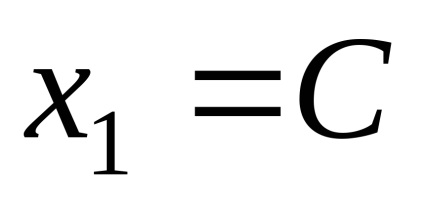
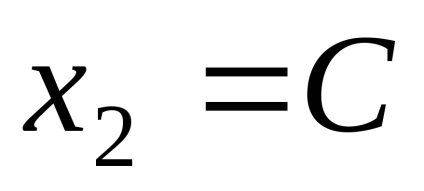
De unde vectorii proprii corespund valorii proprii
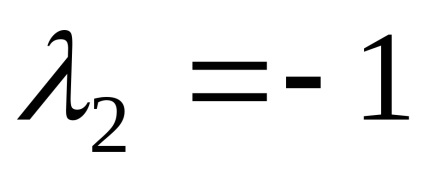
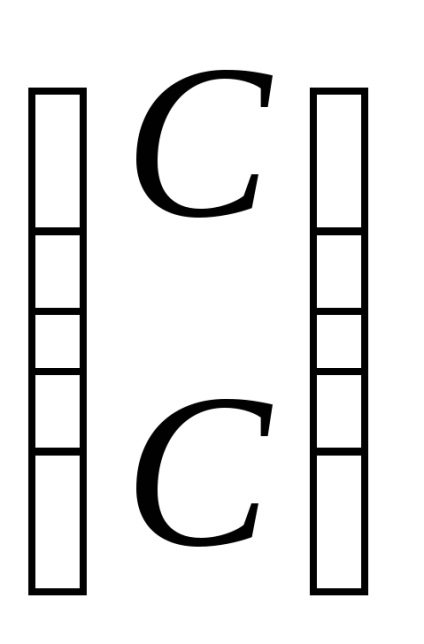
Răspuns. Valoare proprie
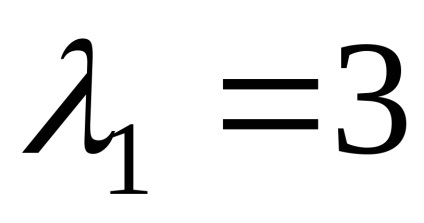
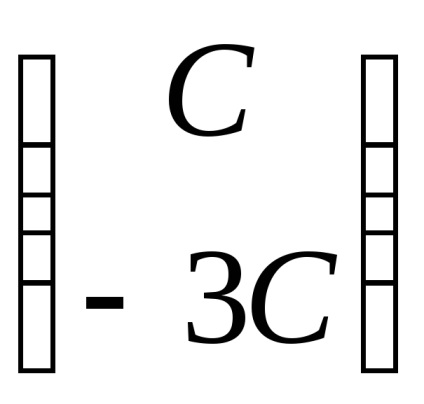
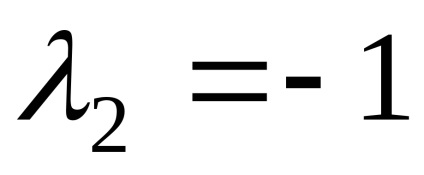
Exemplul 3. Găsiți valorile proprii și vectorii proprii ai unui operator liniar. dat într-o anumită bază de matricea A =
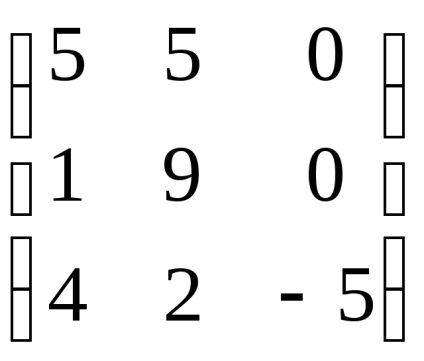
Să găsim valorile proprii ale unui operator liniar. Pentru a face acest lucru, formulam ecuația caracteristică și găsim rădăcinile ei:
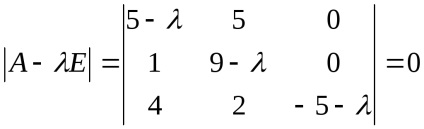
,
,
,
,
, ,
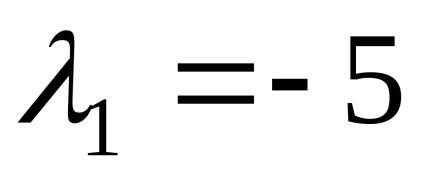
Să găsim vectorii proprii care corespund valorii proprii
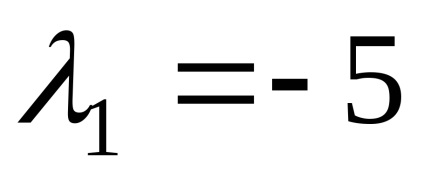
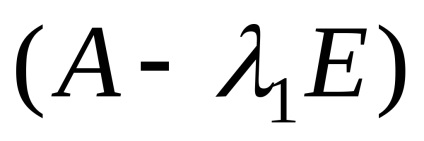
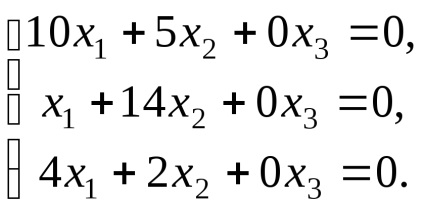

Deoarece rangul matricei sistemului (r = 2) este mai mic decât numărul de necunoscute, sistemul are un set infinit de soluții. Scriind sistemul transformat și rezolvându-l,
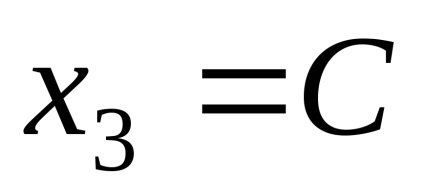
Astfel, vectorii proprii corespund valorii proprii
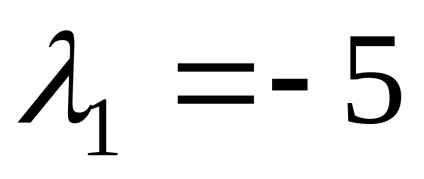
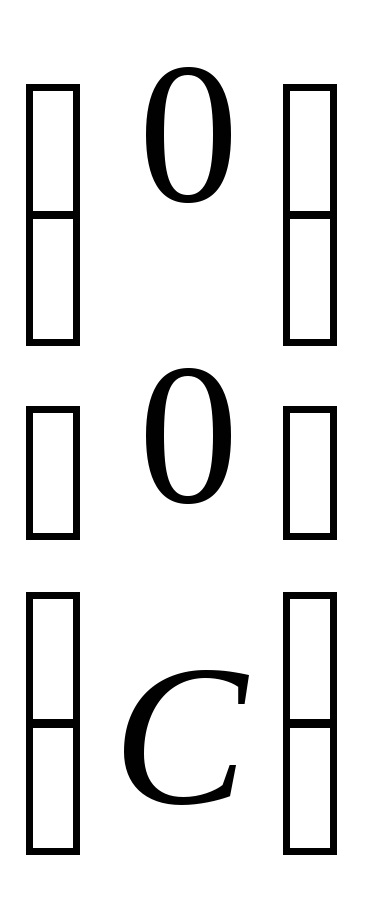
Să găsim vectorii proprii care corespund valorii proprii
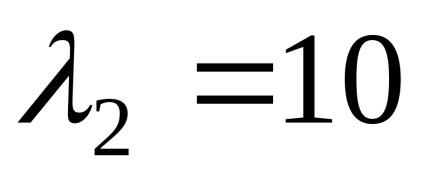
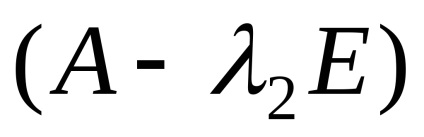
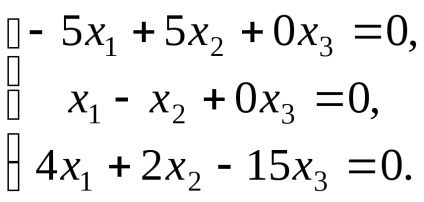
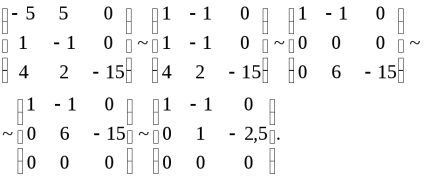
de unde, sistemul ia forma
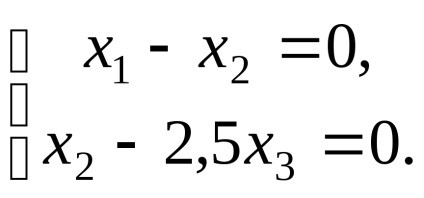
Astfel, vectorii proprii corespund valorii proprii
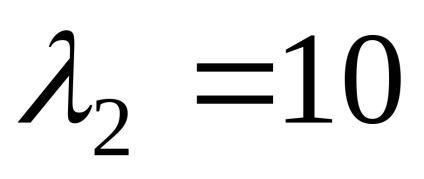
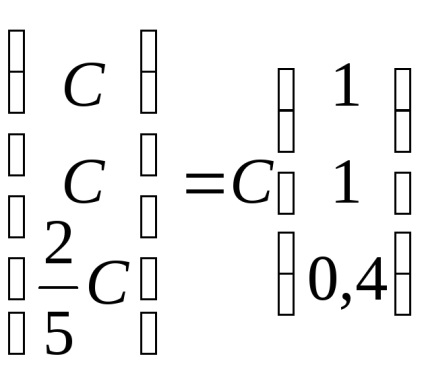
Să găsim vectorii proprii care corespund valorii proprii
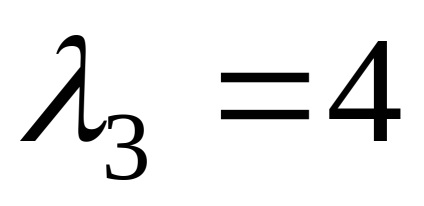
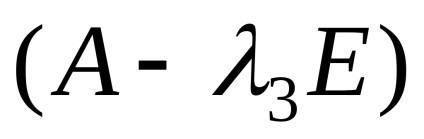
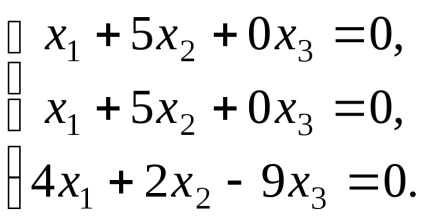
,
de unde, sistemul ia forma
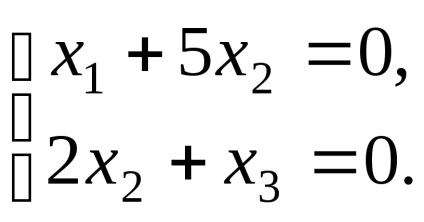
Astfel, vectorii proprii corespund valorii proprii
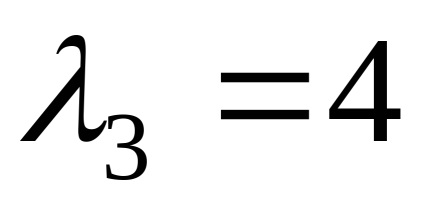
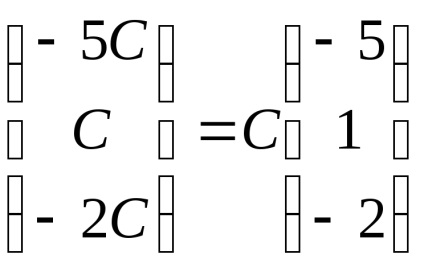
Articole similare
-
Semnificația numelui agvan este originea și interpretarea numelui
-
Semnificația numelui Abigail este originea și interpretarea numelui
-
Semnificația numelui Araxia este originea și interpretarea numelui
Trimiteți-le prietenilor: