Istoria teoremei pitagoreene este interesantă

și

Istoria teoremei lui Pitagora este interesantă. Deși această teoremă este legată de numele lui Pythagoras, ea era cunoscută cu mult înainte de el. În textele babiloniene, această teoremă are loc cu 1200 de ani înainte de Pythagoras, iar în Egipt acest raport a fost folosit pentru a construi un unghi drept acum cinci mii de ani. Este posibil ca la acel moment dovezile ei să nu fi fost încă cunoscute, iar relația dintre hypotenuse și picioare a fost stabilită experimental pe baza măsurătorilor. Pitagora, aparent, a găsit o dovadă a acestei relații. Păstrarea tradiției antice că, după deschiderea lui Pitagora a sacrificat un taur pentru zei, în conformitate cu alte dovezi - chiar și o sută de tauri. În secolele următoare au fost găsite diverse alte dovezi ale teoremei pitagoreene. În prezent, există mai mult de cinci sute, inclusiv: geometric, algebric, mecanic și altele. Datorită acestei dovezi, teorema lui Pitagora a căzut în Cartea Recordurilor Guinness, ca o teoremă cu cele mai multe dovezi. Acest lucru demonstrează interesul neîngrădit pentru el din comunitatea matematică largă. Teorema pitagoreană a servit drept sursă pentru multe generalizări și idei fertile. Adâncimea acestui adevăr vechi, aparent, este departe de a fi epuizată.

Există așa-numitele pitagoreice copac - un copac ipotetic, care este compus din triunghi dreptunghiular interconectate, cu un picior și construit pe pătratele ipotenuzei.

Teorema lui Pitagora are o consecință pentru un triunghi arbitrar:
latură a triunghiului este egală cu rădăcina pătrată a sumei pătratelor celorlalte două din laturile sale minus de două ori produsul laturile cosinusul unghiului dintre ele.
Sub forma unei formuli, este scris astfel:

a 2 = b 2 + c 2 - 2 bc * cos α

Această consecință este denumită, de obicei, teorema cosinus, dar, de fapt, este teorema lui Pythagorean pentru un triunghi arbitrar.

Există trei formulări ale teoremei pitagoreene:

1. Într-un triunghi dreptunghiular, pătratul hypotenusei este egal cu suma pătratelor picioarelor.

2. Pătratul pieței construit pe hypotenuse a unui triunghi în unghi drept este egal cu suma pătratelor pătrate construite pe picioare.

3. Piața construit pe ipotenuzei unui triunghi dreptunghic, pătrate equidecomposable construit pe Catete.

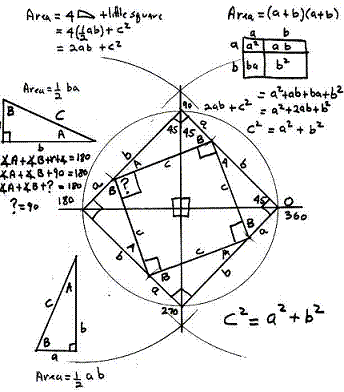
Figura arată două pătrate egale. Lungimea laturilor fiecărui pătrat este a + b. Fiecare dintre pătrate este împărțită în părți formate din pătrate și triunghiuri dreptunghiulare. În mod evident, în cazul în care zona de pătrat ia zona cvadruplu drept triunghi cu picioare a, b, va rămâne în zone egale, adică. E. C2 = a2 + b2. Cu toate acestea, vechii hinduși cărora le aparține acest raționament, de obicei, nu l-au înregistrat, ci au însoțit desenul cu un singur cuvânt: "Uite!" Este posibil ca Pitagora să propună aceeași dovadă.

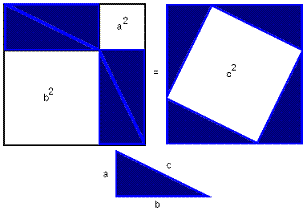
2) Dovada an-naurisiei *

Dovada An-Narysia este, de asemenea, destul de ușoară. Este demn de remarcat faptul că toate cifrele coincid cu cele egale cu acestea numai în cazul transferului paralel.
D

da: atunci când se împarte în cifre, este necesar să se ia în considerare faptul că DE = BF.
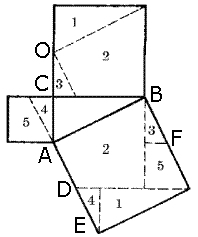
dovada:
Desenul arată clar că smochinele. marcate cu aceleași numere, sunt egale. Triunghiurile 1 și 1, 3 și 3, 4 și 4 sunt egale unele cu altele. Cvadranglele 2 și 2, 5 și 5 sunt de asemenea egale. În consecință, teorema este demonstrată.

* - Denumire romanizată - Annanități.

3) O dovadă posibilă a lui Pitagora

Printre dovezile teoremei pitagoreene, primul loc (probabil cel mai vechi) printr-o metodă algebrică este dovada folosind o asemănare. Vom prezenta în prezenta prezentă una dintre astfel de dovezi, eventual aparținând lui Pythagoras.
Dată: ΔАВС - dreptunghiulară cu un unghi drept C; CM - înălțime; b1 - proiecția piciorului b pe hypotenuse, a1 - proiecția piciorului a pe hypotenuse.
Dovada: Din faptul că ΔABC este similar cu ΔACM, urmează:

din faptul că ΔABC este similar cu ΔBCM urmează:

Termenul Folding prin termenul ecuației (1) și (2), obținem un 2 + b 2 = CB1 + CA1 = c (b1 + a1) = c 2 .Teorema dovedit.
Dacă Pitagora a oferit într-adevăr o astfel de dovadă, el a fost familiarizat cu un număr de teoreme geometrice importante pe care istoricii moderni de matematică este de obicei atribuite Euclid.

3) Dovada lui Garfield

Dată: Două triunghiuri dreptunghiulare.
Dovada: În ilustrație, trei triunghiuri dreptunghiulare constituie un trapez. Prin urmare, aria acestei cifre poate fi găsită prin formula zonei unui trapez dreptunghiular sau ca sumă a suprafețelor a trei triunghiuri. În primul caz, această zonă este

și în al doilea caz

ab / 2 + ab / 2 + c 2/2.

Ecuating aceste expresii, vom obține teorema Pitagora.

4) Dovada se bazează pe teoria similitudinii.

În triunghiul drept ABC, desenați CD-ul de înălțime din vârful unghiului drept; apoi triunghiul este împărțit în două triunghiuri, care sunt de asemenea dreptunghiulare. Triunghiurile rezultate vor fi similare unul cu celălalt și cu triunghiul original. Acest lucru este ușor de dovedit folosind primul semn al asemănării triunghiurilor (la două unghiuri). De fapt, se poate vedea că în afară de dreptul de triunghiuri unghi ABC și ACD au un unghi comun o, triunghiurile ABC și CBD - total unghi b. Faptul că triunghiurile mici sunt, de asemenea, similare unul cu celălalt, rezultă din faptul că fiecare dintre ele este similar cu un triunghi mare. Cu toate acestea, acest lucru poate fi stabilit direct.
pentru că Picioarele unui triunghi dreptunghiular sunt mediul geometric între hypotenuse și proiecția piciorului la hypotenuse, avem:

Adăugând aceste termene egale pe termen, obținem:

Teorema este dovedită din nou.

Nicola Leonard Sadu Carnot (1824)

Articole similare

Pagina anterioară