La examinarea fiecărei întrebări, există cantități constante și variabile.
Cantități care nu își schimbă mărimea atunci când iau în considerare o întrebare se numesc constante.
Variabile de cantitate. Cantitățile care își pot schimba valoarea sunt numite variabile.
În cazul în care un anumit cerc, raza constanta de cerc, coardă este un cerc care trece prin orice punct de pe cerc, este variabil.
In mod similar, cu creșterea apotemă număr corect de laturi ale poligonului descris le rămâne constantă, iar valoarea perimetrelor variabile.
Variabilele variază în limite.
Valoare aproximativă. Când variabilă în timpul schimbării sale prin creșterea sau scăderea se apropie de o valoare constantă, astfel încât diferența dintre ea și constanta poate fi făcută mai mică decât orice dimensiune dată, aceasta se numește o cantitate se apropie.
Valoarea constantă la care se apropie o variabilă se numește limita sa.
Limita. Limita este definită ca fiind o valoare constantă, care este aproape de cealaltă variabilă creștere sau în scădere, dar niciodată nu ajunge, deși diferența poate fi făcută mai mică decât orice mărime dată.
Metoda limitelor. Setul de proprietăți pe care se apropie cantitățile și limitele lor și aplicarea acestor proprietăți la rezolvarea diferitelor întrebări se numește metoda limită.
De la definirea limitei, urmatoarele proprietati ale limitelor:
Limita este o valoare constantă.
Cantitatea care se apropie este întotdeauna mai mare sau mai mică decât limita.
Diferența dintre cantitatea care se apropie și limita sa poate fi mai mică decât orice valoare dată.
Suma unghiurilor unui poligon obișnuit având n laturi este exprimată prin formula:
S = 2d (n-2) = 2-4d
Valoarea fiecărui unghi va fi
Această valoare a lui A este o variabilă. Se modifică odată cu creșterea numărului de laturi ale poligonului obișnuit.
În această expresie, numărul 2d are toate cele trei proprietăți ale limitei:
În primul rând, cantitatea 2d este o valoare constantă.
În al doilea rând, valoarea apropiată a lui A este întotdeauna mai mică decât 2d și
în cele din urmă, diferența (4d) / n cu creșterea n poate fi făcută mai mică decât orice valoare dată.
Odată cu creșterea numărului de laturi ale unui poligon regulat al valorii sale toate unghiurile A, crescând și mai mult, mai aproape de două linii și două linii există o limită la care se tinde la această valoare.
Dacă în ecuația X = K + α cantitatea α poate fi făcută mai mică decât orice cantitate dată și K este o valoare constantă, atunci X este o cantitate care se apropie și K este limita sa.
Limita este notată cu cuvântul lim. (limită) sau înainte. (limită), stabilită înainte de amploarea apropierii.
Astfel scriu
K = lim X = lim (K + α)
Din această relație este clar că
O cantitate infinit de mică este o variabilă care are limita zero.
Următoarele teoreme sunt importante în metoda limită.
Teoremă 129. Dacă două valori aproximative sunt egale, atunci limitele lor sunt egale.
Este dat. Fie X și Y două cantități aproximative, A și B limitele lor, astfel încât
X = A + a, Y = B + β
Variabilele α și β pot fi făcute mai puțin decât orice valoare dată.
Dovada. Din faptul că cele două cantitati apropiate X și Y sunt egale, egalitatea X = Y sau Y
Aici pot apărea următoarele trei ipoteze:
A> B, A
1. Dacă există o inegalitate A> B, atunci diferența A - B ar fi egală cu o anumită constanță finită k.
Deoarece α și β poate scădea la infinit, nu se poate presupune că p difference - alfa egală cu o valoare constantă finită k, în consecință, inegalitatea A> B nu este posibilă.
2. În mod similar, inegalitatea A
unde l este o valoare finită constantă.
Din egalitatea (a) rezultă că
Această inegalitate este la fel de imposibilă, deci presupunerea A Astfel, numai egalitatea rămâne valabilă: A = B (BTD). Teorema 130. Raportul dintre cantitățile care se apropie este egal cu raportul dintre limitele lor. Două cantități aproximative sunt date X = A + α și Y = B + β Este necesar să se demonstreze că X / Y = A / B. Dovada. Raportul celor două cantități apropiate va fi Indicați valoarea finită a acestui raport cu l, apoi A + α este o cantitate apropiată având limita A; Bl + Bβ este o cantitate aproximativă având limita valorii lui Bl. Pe baza teoremei precedente, egalitatea (1) conduce la egalitate În consecință, l = A / B din care (A + α) / (B + β) = A / B (BTD). Teorema 131. Linia poligonală exterioară este mai mare decât curba convexă din interiorul liniei poligonale.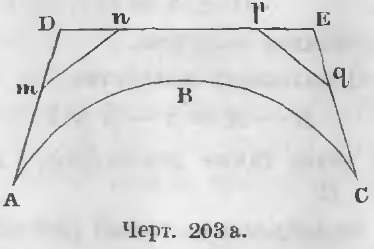
Dovada. Dacă curba ABC nu este mai mică decât orice poligon extern (Fig. 203), atunci ar exista un astfel de poligon extern, care ar fi fost mai mică decât oricare altă curbă ABC poligonal externă și, prin urmare, mai puțin.
Lăsați ADEC să fie o astfel de linie întreruptă.
În acest caz, este întotdeauna posibil să se petreacă ca segmente Mn, PQ, astfel încât acestea nu traversează curba ABC, apoi a format un nou polilinie AmnpqC, care este mai mică decât ADEC, pentru
mn Adăugând la aceste inegalități cantitățile Am, np, qC, obținem: mn + pq + Am + np + qC Astfel, prezumția că există o linie poligonală exterioară mai mică decât o curbă nu se păstrează. De aici rezultă corolarul. Perimetrul poligonului descris este mai mare decât un cerc. Teorema 132. Diferența dintre perimetrul unui poligon cu același nume descris și înscris împreună cu numărul de laturi poate fi făcut mai mic decât orice valoare dată. Notând cu P și p perimetrele poligonului descris și inscripționat cu n laturi (Figura 204), știm că (P - p) / p = (OA - Oa) / Oa, (P - p) / p = Aa / Oa, P - p = (Aa / Oa) p (a) Perimetrul orice poligon poligon mai lung perimetru, care constă în aceea, perimetrul p mai mic decât perimetrul unui pătrat descris. Perimetrul pătratului descris este 8 · Oa (8 raze), deci p <8 · Oa. Introducerea 8 · Oa în cea de-a doua parte a egalității (a) în loc de p, o creștem, prin urmare, P - p <8 · Oa · (Aa/Oa) или Prin dublarea numărului de laturi Aa lungimea segmentului pot fi realizate mai mici decât orice mărime dată, pentru dublarea numărului de laturi ale unghiului AOB, și, prin urmare, unghiul de AON sunt reduse, iar înclinat AO se apropie perpendicular pe nO, astfel încât diferența dintre indirectă și perpendiculara poate fi făcută mai mică decât de orice magnitudine. Teorema 133. Pe măsură ce crește numărul de laturi, perimetrele poligoanelor descrise și inscripționate se apropie de aceeași limită. Dovada. Din inegalitate Odată cu dublarea numărului de laturi, perimetrul poligonului descris scade, iar perimetrul înscrisului crește. Deoarece limita lui Aa este 0, limita (P - p) = 0. P = prev. p sau lim P = lim p (PTC). Teorema 134. Un cerc este limita perimetrilor poligoanelor înscrise și descrise. Atunci când dubla numărul de laturi, perimetrul poligonului obișnuit descris scade, iar perimetrul celui înscris crește. În acest caz, perimetrul poligonului descris este mai mare, iar inscripția este mai mică decât un cerc. Deoarece diferența dintre perimetrul poligonului circumscris și inscripționată poate fi făcută mai mică decât orice valoare dată, atunci cu siguranță cu gradual dublarea numărului de laturi ale diferenței dintre perimetrele poligoane regulate descrise și o circumferință, precum și între circumferința și circumferințele inscripționată poligoane regulate pot fi mai mici decât orice valoare dată , prin urmare: Un cerc este limita perimetrilor poligoanelor inscripționate și descrise. Teorema 135. Cercurile sunt proporționale cu razele. Dovada. Indicați lungimile a două cercuri prin O și O ', raza lor prin R și R'. Să adăugăm poligoane regulate cu n laturi în ambele cercuri. Denumind perimetrele lor de Pn și Pn, avem egalitatea atunci ecuația precedentă dă Odată cu creșterea treptată a numărului de laturi diferențe a și β între cercurile și circumferințele inscriptionate poligon poate fi făcută o importanță mai mică această valoare, prin urmare, diferența dintre O - α, O „- valorile p se apropie, iar cantitățile O și O“ a limitelor lor. Pe baza teoremei 130, avem egalitatea (O - α) / (O '- β) = O / O', de la Pe baza O / R = O '/ R' sau O / 2R = O '/ 2R' consecința urmează. raportul dintre fiecare cerc și diametrul său este o valoare constantă. Acest raport constant al circumferinței la diametru este numit litera π. Circumferința este egală cu raza înmulțită cu 2π. Aici lungimea este exprimată în aceleași unități în care este exprimată raza. Numărul abstract al π este o cantitate incomensurabilă. Mărimea aproximativă a lui 22/7 este dată de Archimedes. Ea exprimă adevărata valoare a lui π la 0,01. Mecius, care a trăit la sfârșitul secolului al XVI-lea, a găsit pentru o valoare aproximativă de 355/113 = 3,141592 cu o precizie de 0,000001. Această relație este ușor de reținut dacă este prezentată sub formă Lungimea arcului având n grade. Circumferința are 360 °. Lungimea unui cerc de rază R este exprimată prin formula 2πR. Lungimea unui grad va fi valoarea (2πR) / 360. Notând cu lungimea unui arc de n grade, avem: Formula (a) se referă la trei cantități: n numărul de grade al arcului, lungimea lui și R raza cercului. Aceasta face posibilă determinarea uneia dintre ele de celelalte două. O formulă care exprimă circumferința unui cerc, ia pentru R = 1 formularul din care se poate observa că 2π expune lungimea unui cerc descris de o rază egală cu una. Pentru a determina π, se calculează perimetrele poligoanelor regulate înscrise și descrise cu același număr de laturi. Circumferința se află între perimetrele acestor poligoane. Este mai mică decât circumferințele poligoanelor circumscrise și mai multe perimetre. Diferența dintre perimetre va indica în ce măsură se află eroarea în definirea cercului și deci în definiția lui π. Pentru a reduce această eroare în definirea lui π, se calculează succesiv perimetrele poligoanelor cu dublul numărului de laturi. Diferența dintre perimetrele lor va fi mai mică și mai mică și, prin urmare, precizia cu care se poate determina crește. Denumirea lungimii laterale a poligonilor obișnuiți având laturi n inscripționate printr-o. descrisă de An și de raza de r, folosim formula pentru a determina lungimea laterală a unui poligon inscripționat cu dublul numărului de laturi: ci pentru a determina partea poligonului descrisă de-a lungul laturii înscrise de formula: Notând cu Pn și pn perimetrele poligonului obișnuit descris și inscripționat, avem: Valoarea aproximată a lui π satisface inegalitățile: în care an și An sunt calculate pentru un cerc cu o rază egală cu 1, deci r = 1 în formulele care le definesc. Formulele (1) și (2) pentru r = 1 au forma: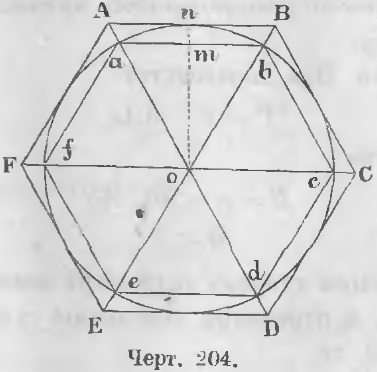
P - p <8AaDefiniția lui π
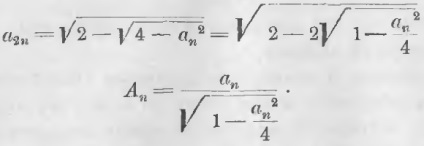
Presupunând că n = 6, pentru a6 de partea unui hexagon regulat înscris pentru r = 1, avem:

Înmulțind aceste valori cu numărul de laturi, avem următorul tabel de perimetre ale poligoanelor normale inscripționate și descrise ale numărului corespunzător de laturi, calculat cu până la 6 zecimale

Din acest tabel vedem că diferența dintre perimetrele poligoanelor obișnuite înscrise și descrise scade.
Pentru un 96-gon, el este deja mai mic decât 0,01, iar pentru un poligon cu 3072 laturi, acesta este mai mic decât 0,00001.
Arhimedes a stabilit calculul laturii celor 96 de goni și a dat o valoare aproximativă lui π la 0,01. Mecii a dat pentru π o valoare de π = 355/113 = 3.1415920 cu o precizie de 0.000001.
Articole similare
Trimiteți-le prietenilor: