În ceea ce predecesorii Apollonios de inovare reflectate, în special, în comunitatea cu care a abordat subiectul său. În primul rând, Apollonios secțiuni conice definite ca planul de secțiune, care nu este neapărat perpendicular pe con.
Mai mult decât atât, Apollonios, așa cum sa spus, și a considerat al doilea aspect al hiperbola, iar acest lucru a luat în considerare faptul că conul este împărțit în două cavități. Acest lucru era necesar pentru ca teoriile să aibă comunitatea dorită - altfel ar fi trebuit să facem prea multe excepții. Astfel parabolei a încetat să fie o secțiune de numai un con unghi obtuz, elipsa - o acută și hiperbolă - obtuz. Mai mult decât atât, Apollonios considerat nu numai un con circular drept (adică, cele în care perpendiculara a scăzut de la partea de sus, trece prin centrul bazei), dar conuri arbitrare și circulare.
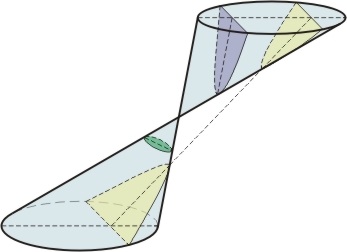
Fig. 1. Secțiuni de conuri din Apollonium
Apollonius a arătat că nici unul dintre planurile de con secționale arbitrar duce numai la aceste trei tipuri de curbe (cu excepția unor cazuri degenerate, de exemplu, atunci când secțiunea transversală constă dintr-o pereche de linii intersectate). De aceea a trebuit să schimbe terminologia: „hiperbolă“ în loc de „o secțiune transversală dreptunghiulară (o, obtuz acută) con“ Apollonios a introdus termenii „parabole“, „elipsa“, În ultima lecție, am văzut că acești termeni sunt legați de forma ecuațiilor ("simptome") care determină această secțiune. Apollonius a arătat că relația dintre coordonate, exprimată prin simptomul acestei secțiuni:
y 2 = 2 px pentru parabola,
y 2 = 2 px - (p / a) x 2 pentru elipsă,
y 2 = 2 px + (p / a) x 2 pentru hiperbola,
nu se modifică dacă axa absciselor este luată nu numai de axa secțiunii conice.
Aici este necesar să introducem un nou termen. Diametrele unei elipse sau a unei hiperbola sunt orice segmente care trec prin centrul unei elipse sau hiperbola. (Sper că înțelegeți ce este centrul de hiperbole Este centrul său de simetrie. - punctul de intersecție al asymptotes) și diametrul parabolei este orice linie dreaptă paralelă cu axa parabolei (de exemplu, intersectându unei parabole, la un singur punct). Deci, Apollonios a aratat ca simptom al secțiunii conica va avea același fel, în cazul în care axa x este un diametru arbitrar al secțiunii conice și axa y - a tangentei la un capăt al acestui diametru. Astfel, nu ar mai coordonate rectangulare vor abscisă diametrul segmentelor și ordonată - poluhordami paralelă cu tangenta respectivă. (Secțiunile conice au proprietatea că acordurile paralele cu această tangentă sunt împărțite în jumătate de diametrul dat).
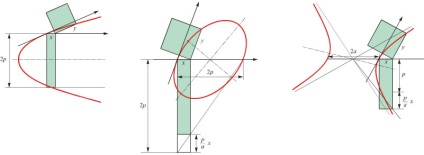
Fig. 2. Forma ecuațiilor de secțiuni conice este păstrată în coordonatele formate prin diametru și tangent
În cazul unei elipse și a unei hiperbola, pentru fiecare diametru este posibil să se determine diametrul său conjugat, adică un diametru paralel cu diametrul tangențial desenat la capetele diametrului inițial.
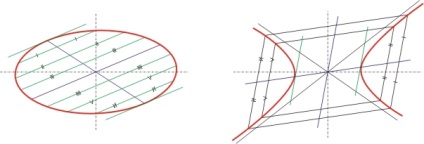
Fig. 3. Diametre conjugate
Diametrele conjugate joacă un rol important în teoria lui Apollonia. În special, el susține că:
- suma pătratelor diametrelor conjugate ale elipsei este constantă;
- Un paralelogram construit pe diametrele conjugate ale unei elipse are o arie constantă.
Apollonius mult preocupat forma ecuațiile secțiunilor conice în raport cu axele de coordonate coincid cu două diametre diferite, în special conjugat. În notație modernă, ecuația elipsa și hiperbola în raport cu diametrul conjugat (așa-numita ecuație centrală a elipsei și hiperbola) sunt după cum urmează:
x 2 / a 2 + y 2 / b 2 = 1 (elipsă),
Articole similare
Trimiteți-le prietenilor: