Interpolarea cu polinoame algebrice

Interpolarea cu polinoame algebrice a funcției f (x) pe intervalul [a, b] este construcția unui polinom Pn (x) cu grad mai mic sau egal cu n. recepție la nodurile de interpolare x0. x1. xn valorile lui f (xi):

Pn (xi) = a 0 + a 1 x i + a 2 x i 2 +. + a n x i n = f (x i). i = 0. 1. n (x _) = a_ + a_x_ + a_x _ ^ +. + a_x _ ^ = f (x_), \ quad i = 0,1. n>

Este nonzero pentru orice valoare pereche distinctă a lui xi. iar interpolarea funcției f de la valorile sale la nodurile xi cu ajutorul polinomului Pn (x) este întotdeauna posibilă și unică.

Formula de interpolare obținută f (x) ≈ P n (x) (x)> este adesea folosită pentru calcularea aproximativă a valorilor funcției f pentru valorile argumentului x. altele decât nodurile de interpolare. În acest caz, interpolarea se distinge în sens restrâns, când x ∈ [x 0. x n], x_ \ right]>. și extrapolare. atunci când x ∈ [a. b]. x ∉ [x 0. x n], x_ \ dreapta]>

Să presupunem că n punctele P 1 sunt date în spațiu. P n, P_, \ puncte, P_>. care în unele sisteme de coordonate au vectori radiali r 1. r 2. .... r n _, \ mathbf _, \ dots, \ mathbf _>.

Problema interpolării constă în construirea unei curbe care trece prin punctele indicate în ordinea indicată.

Printr-un set fix de puncte, un număr infinit de curbe poate fi desenat, astfel încât problema interpolării nu are o soluție unică.

Introducerea parametrizării și a rețelei poate fi efectuată în mai multe moduri. În mod normal, fie este aleasă o rețea uniformă, presupunând a = 0. b = n - 1. t i = i - 1 = i - 1>. sau, mai preferabil, să conecteze punctele prin segmente și să ia lungimea segmentului r i + 1 - r i - - mathbf -> ca diferență a valorilor parametrului t i + 1 - t i - t>.

Una dintre metodele comune de interpolare este folosirea unei curbe sub forma unui polinom în t de grad n - 1. care este, ca o funcție

Aceste condiții conduc la un sistem de ecuații liniare pentru coeficienții a k>

Să fim atenți că este necesar să rezolvăm trei sisteme de ecuații: pentru x. y și z coordonate. Toate acestea au aceeași matrice de coeficienți, inversând care, în funcție de valorile vectorilor de rază r i> puncte, se calculează vectorii a k> din coeficienții polinomului. Determinantul matricei

W (t 1. t 2. .... T n) = | 1 t 1 t 1 2 ... t 1 n - 1 1 t 2 t 2 2 ... t 2 n - 1 ⋮ ⋮ ⋮ ⋮ 1 t n t n 2 ... t n n - 1 | = Π i. j. i> j (t i - t j), t, ldot, t _) = 1t_t _ ^ \ ldots t _ ^ \\ 1t_t _ ^ \ ldots t _ ^ \\\ vdots \ vdots \ vdots \ vdots \\ 1t_t _ ^ \ ldots (t-t)>

se numește determinantul Vandermonde. Dacă nodurile rețelei nu coincid, este diferită de zero, astfel că sistemul de ecuații are o soluție.

În plus față de inversarea directă a matricii, există mai multe modalități de calcul al polinomului de interpolare. Din cauza unicității polinomului, vorbim despre diferite forme ale înregistrării sale.

• Pentru un anumit set de puncte și o rețea de parametri, curba este construită în mod unic.
• Curba este interpolare, adică trece prin toate punctele date.
• Curba are derivate continue de orice ordine.

• Cu un număr tot mai mare de puncte, ordinul polinomului crește, iar cu acesta crește numărul operațiilor care trebuie efectuate pentru a calcula punctul de pe curbă.
• Pe măsură ce crește numărul de puncte din curba de interpolare, pot apărea oscilații (a se vedea exemplul de mai jos).

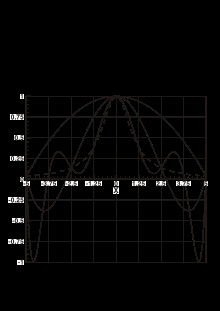
Interpolarea pe o secvență de grile. Exemplu de exemplu.

Un exemplu clasic (Runge), arătând apariția oscilațiilor într-un polinom de interpolare, este o interpolare pe o rețea uniformă de valori ale funcției

care la punctele x i> ia valori y i = 1 / (1 + x i 2) = 1 / (1 + x _ ^)>. Figura prezintă graficele funcției în sine (linia punctată punctuală) și trei curbe de interpolare pentru n = 3. 5. 9:

• interpolarea pe grilă x 1 = - 5. x 2 = 0. x 3 = 5 = -5, x_ = 0, x_ = 5> este o parabolă patratică;
• interpolarea pe grilă x 1 = - 5. x 2 = - 2.5. x 3 = 0. x 4 = 2.5. x 5 = 5 = -5, x_ = - 2,5, x_ = 0, x_ = 2,5, x_ = 5> este un polinom de gradul patru;
• interpolarea pe grila x 1 = - 5. x 2 = - 3.75. x 3 = - 2,5. x 4 = - 1,25. x 5 = 0. x 6 = 1,25. x 7 = 2,5. x 8 = 3,75. x 9 = 5 = -5, x _ = - 3,75, x _ = - 2,5, x _ = - 1,25, X_ = 0, X_ = 1,25, X_ = 2,5, X_ = 3,75, X_ = 5> - un polinom de gradul opt.

Valorile polinomului de interpolare, chiar și pentru funcțiile netede la punctele intermediare, pot să se abată puternic de valorile funcției însăși.

Trimiteți-le prietenilor: