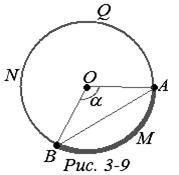
Fie mai puțin decât un semicerc și deci d (A, B) este lungimea acestui arc. Indicăm prin valoarea AOB unghiulară susținută pe arcul AMB și prin r (A, B) lungimea segmentului AB. După cum știți,
AOB (Figura 3-9) găsim:
Din formulele (1), (2) rezultă că:
3. O mișcare a unei sfere este orice cartografie izometrică a acestei sfere în sine, adică o mapare f. S ® S, care satisface următoarea condiție: pentru orice punct A și B al sferei, d (A, B) = d (f (A), f (B)). Rezultă din (3) că în acest caz r (A, B) = r (f (A), f (B)). În consecință, orice mișcare f a sferei S este generată de o mișcare f0 a spațiului și f0 (0) = 0. În schimb, orice mișcare g0 a spațiului care părăsește punctul O invariante generează o mișcare definită a sferei S.
Prin urmare, concluzionăm că setul tuturor mișcărilor sferei S este un grup care este izomorf cu subgrupa staționară H0 a punctului O în grupul de mișcări ale spațiului.
Două figuri F, F 'Ì S se spune că sunt congruente sau egale dacă există o mișcare a sferei S care ia una din aceste figuri în alta. În consecință, figurile F, F ' Ì S sunt congruente dacă sunt echivalente cu H0.
4. Luăm pe sfera S trei puncte A, B, C care nu se află pe un cerc mare. Ele definesc trei emisfere, fiecare dintre ele conținând puncte A, B, C, cu două dintre aceste puncte aparținând marginii emisferei. Intersecția acestor trei emisfere este numită un triunghi sferic cu vârfurile A, B, C. Arcurile AB, BC, AC de cercuri mari (semicercuri mai mici) se numesc laturile triunghiului sferic ABC.
Fie ABC - triunghi sferic, a = d (B, C), b = d (A, C), cu = d (A, B) - lungimea laturilor sale, a, b, g, respectiv unghiurile AOC BOC și AOB.
Să demonstrăm teorema sinusoidală pentru un triunghi sferic.
Teorema. Să presupunem că a = d
Se poate demonstra că se menține următoarea egalitate, care exprimă teorema cosinusului pentru triunghiul sferic ABC:
De asemenea, puteți demonstra că aria triunghiului sferic ABC este calculată prin formula
unde este așa-numitul exces al unui triunghi sferic. Din zona SABC> 0, rezultă din formula (8) că e> 0, adică. Astfel, suma unghiurilor oricărui triunghi sferic este mai mare decât p. Aceasta este o diferență esențială între geometria pe sferă atât din geometrie pe planul euclidian, cât și din geometria pe planul Lobachev
Modelul Poincaré de geometrie Lobachevsky. (Omul de știință francez Henri Poincaré (1854-1912) - cel mai mare model matematician descris mai târziu, a fost oferit pentru a le în 1882 ..) Rolul jucat de planul Lobachevsky semi-deschis; rolul directe operează conține un semicerc centrată pe limitarea razele directe și perpendicular pe această linie. Rolul suprapunerii se realizează prin compoziții de inversiuni cu privire la aceste semicercuri și reflexii în raze. Geometria Totul Axiom euclidiană sunt efectuate, cu excepția axioma paralele (Fig. 4-1, precum și), deci în acest model se realizează geometria Lobachevskian.
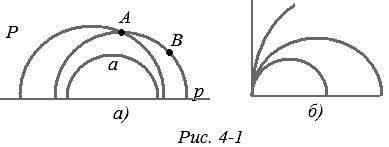
Să descriem acest model mai detaliat și să dovedim ceea ce sa spus. Noi luăm pe planul euclidian de obicei orice linie p și deschis pe jumătate linia de p R. limitat este numit o linie de delimitare. P-avionul P va juca rolul avionului Lobachevsky; îl vom numi un "avion" în ghilimele. Punctele în modelul va fi punctul de acest „plan“, adică. E. R. Pentru semiplanul „directă“, în modelul acceptat, în primul rând, conținute în semicercuri P ale căror centre se află pe linia de delimitare (fig. 4-1, a). "Segmentul" AB din model este arcul unui astfel de semicerc cu puncte finale A, B.
Subliniem că sfârșitul "segmentului" nu poate fi sfârșitul unui semicerc care reprezintă o linie dreaptă; capetele sale sunt excluse impreuna cu linia de granita; Un "avion" este o jumătate de avion deschis. Punctul "drept" servește ca început comun al a două "raze" - două arce de semicerc (cu capetele excluse). "Unghiul" este o figură a două "raze" cu origine comună, care nu sunt cuprinse într-o singură "linie dreaptă" (Figura 4-1, a).
În plus față de aceste "directe" există și "directe" - acestea sunt jumătăți de linie perpendiculare pe linia de graniță. Acestea sunt limitele semicercurilor considerate (Figura 4-1, b). Când centrul semicercului este îndepărtat de-a lungul liniei de graniță, iar semicercul trece prin punctul dat, acesta se "îndreaptă", iar în limita se trece în jumătatea liniei. Prin urmare, vom continua să credem aceste semilogii printre modelele "directe" ca semicercuri, ca "semicercuri de rază infinită". Acest lucru va face posibilă renunțarea la rezervele plictisitoare privind aceste jumătăți de linii și, cu toate acestea, trebuie să ne amintim convenționalitatea acestui lucru și să fim gata să verificăm declarațiile pentru astfel de "semicercuri". ("Segmentul" de pe o astfel de "linie dreaptă" este segmentul obișnuit, iar "razele" sunt o rază obișnuită, cealaltă este un segment cu un capăt exclusiv pe linia de frontieră.)
Considerăm acum în acest model axiomele în care nu intră conceptul de egalitate de segmente și unghiuri.
Axiomul liniilor paralele pentru liniile drepte se referă la astfel de axiome. În acest model, evident, nu este satisfăcut: printr-un punct A care nu se află pe "linia dreaptă" a, trec infinit multe "linii drepte" care nu au puncte comune cu o (fig.4-1, a).
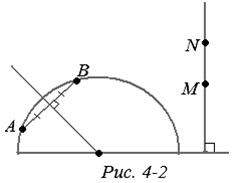
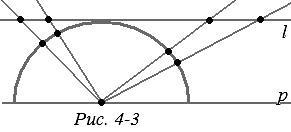
Toate celelalte axiome care vorbesc despre legătura dintre puncte și segmente sau puncte și linii, despre aranjamentul reciproc al punctelor și liniilor, sunt satisfăcute aici. Astfel, în Fig. 4-2 prezintă construcția unui segment cu capete date. Apoi, luăm un semicerc care reprezintă "linia dreaptă" din model. Desenați o linie tangentă la acest semicerc și paralel cu linia de frontieră. Proiectăm un semicerc din centrul său pe linia dreaptă l (figura 4-3). Obținem o corespondență unu-la-unu care păstrează ordinea între punctele liniei și semicercul, adică modelul "drept". Toate proprietățile exprimate în axiome vor fi aceleași. Acestea sunt, de asemenea, evident efectuate pe semilini reprezentând modelele "directe". Axiomul divizării planului este de asemenea satisfăcut. "Straight" - un semicerc - împarte planul în două regiuni - interiorul și cel exterior. Acesta va fi "jumătatea planului" din modelul nostru. De la unul la altul, nu se poate traversa nici un arc fără a traversa "linia dreaptă" - semicercul care le separă.
Trimiteți-le prietenilor: