Integrarea funcțiilor trigonometrice prin intermediul unei substituții trigonometrice universale.
Luați în considerare unele cazuri, găsirea integrantă a funcțiilor trigonometrice. Funcția cu variabile sin x și cos x, peste care se efectuează acțiuni raționale (adunare, scădere, înmulțire și împărțire) sunt de obicei notate R (sin x, cos x), în care R - semn al unei funcții raționale.
Calculul integralelor nedefinite se efectuează la calculul integralelor funcției pioniene prin substituire. care se numește universală.
,
unde R1 (t) este o funcție rațională a lui t. De obicei, această metodă este foarte greoaie, dar întotdeauna duce la rezultat.
În practică, se folosesc și alte substituții mai simple, în funcție de proprietățile (și tipul) funcției integrand. În special, următoarele reguli sunt convenabile:
1) dacă funcția R (sinx; cos x) este impare în raport cu sinxul, adică R (- sinx; cos x) = - R (sin x; cos x), atunci substituția cosx = t raționalizează integralele;
2) dacă funcția R (sinx; cos x) este impare în raport cu cosx, adică R (sinx; -cosx) = -R (sinx; cosx), atunci substituția sinx = t;
3) în cazul în care R funcția (sin x, cos x) este chiar relativ sinx și cosx R (- sin x; - cos x) = R (sin x, cos x), apoi integral raționalizate TGX substituție = t. Aceeași substituție este utilizată dacă integrala are forma
Exemplu Găsiți integrala
Soluție: Facem o substituție universală, apoi dx = ,,. Prin urmare,
Unele substituții trigonometrice speciale.
Integralele de tipul ∫sinmx • cosnx dx
Pentru a găsi astfel de integrale, se utilizează următoarele metode:
1) substituția sinx = t, dacă n este un întreg pozitiv impar întreg;
2) substituția cosx = t, dacă m este un întreg pozitiv impar întreg;
3) formula reducerea ordinului: cos 2 x = 1/2 (1 + cos2x), păcatul 2 x = 1/2 (1-cos 2x), sinx-cosx = 1/2 sin2x, în cazul în care tipul - chiar și numere nenegative;
4) substituția tg x = t, dacă m + n - este un întreg întreg negativ.
Exemplu Găsiți integrala
Soluție: Aplicați substituția sinx = t. Apoi x = arcsint, dx AND
Folosind transformări trigonometrice
Integralele de tipul sunt calculate folosind formulele de trigonometrie binecunoscute:
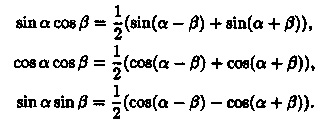
Exemplu Găsiți integralele
Integrarea expresiilor iraționale.
Să luăm în considerare câteva tipuri de integrale care conțin funcții iraționale.
Integralele de tipul sunt numite integrale nedefinite de iraționalități patratice. Acestea pot fi găsite în felul următor:
sub radicalul de a aloca un pătrat complet
și facem substituția x + b / 2a = t. Primele două integrate sunt reduse la tabele, iar cea de-a treia la suma celor două integrale de masă.
Exemplu Găsiți integralele
Soluție: Întrucât,
Facem substituția x + 1/4 = t, x = t-1/4, dx = dt. atunci
Integralele de tipul în care Pn (x) este un polinom de grad n poate fi calculat folosind formula
unde Qn-1 (x) este un polinom de grad n-1 cu coeficienți nedefiniți, este de asemenea un coeficient indefinit.
Toți coeficienții indeterminați se găsesc din identitatea obținută prin diferențierea ambelor laturi ale (1):
după care este necesară echivalarea coeficienților pentru aceleași puteri ale necunoscutului x.
Exemplu Găsiți integralele
Soluție: Prin formula (1) avem:
Diferențiând această egalitate, obținem:
Comparați coeficienții pentru aceleași puteri de x:
Prin urmare, A = -1 / 2, B = 3/2, = 2. Prin urmare,
Integralele de tipul în care a, b, c, d sunt numere reale, , . , sunt numere naturale, se reduc la integrale ale unei funcții raționale prin substituție unde K este cel mai puțin comun multiplu al numerelor fracționate
Într-adevăr, din substituție rezultă că u
adică, x și dx sunt exprimate în termeni de funcții raționale ale lui t. Mai mult, fiecare grad al unei fracții este exprimat în termenii unei funcții raționale a lui t.
Exemplu Găsiți integrala
Soluție: Cel mai mic numar comun al numerelor fracționate de 2/3 și 1/2 este 6.
Prin urmare, am stabilit x + 2 = t 6. x = t 6 -2, dx = 6t 5 dt, Prin urmare,
ExampleShow substituția pentru a găsi integralele:
Soluție: pentru substituția I1 x = t 2. pentru substituția I2
integralelor tip sunt integralele de funcții funcțiilor trigonometrice dependente în mod rațional, folosind următoarele substituții trigonometrice: x = a • pentru prima sint integralei; x = a • tgt pentru cel de-al doilea integral; pentru al treilea integral.
Aici integrandul este o funcție rațională x și alocarea unui radical și complet pătrat pentru a face substituția, integralele acestui tip sunt integralele pascmotpennogo deja tip t. E. La integralelor de tip Aceste integralelor pot fi calculate folosind substituții trigonometrice corespunzătoare.
Exemplu Găsiți integrala
Soluție: Deoarece x 2 + 2 = 4 (x + 1) 2 -5, x + 1 = t, x = t-1, dx = dt. De aceea am stabilit

Notă: Integralul tipului poate fi găsit cu ajutorul substituției x = 1 / t.
Integrarea unui binomial diferențial
Integralele de tip (numite integrale ale unui binomial diferențial), unde a, b sunt numere reale; m, n, p - rațional numerele sunt luate doar atunci când cel puțin unul dintre numerele p, (m + 1) / n sau (m + 1) / n + p este un număr întreg.
Rationalizarea integralului în aceste cazuri se realizează prin următoarele substituții:
1) dacă p este un număr întreg, atunci substituția x = t k. unde k este cel mai puțin comun multiplu al numitorilor fracțiunilor m și n;
2) dacă (m + 1) / n este un număr întreg, atunci substituția unde s este numitorul fracțiunii p;
3) dacă (m + 1) / n + p este un număr întreg, atunci substituția unde s este numitorul deviației p.
În toate celelalte cazuri, integralele de tip nu sunt exprimate în termeni de funcții elementare cunoscute, adică "nu se angajează".
Exemplu Găsiți integralele
Soluție: Din moment ce
Prin urmare, facem o înlocuire
Trimiteți-le prietenilor: