\ (\ blacktriangleright \) Se spune că funcția \ (f (x) \) crește pe intervalul \ (X \). dacă pentru orice \ (x_1, x_2 \ în X \). astfel încât \ (x_1
Se spune că funcția nu se reduce la intervalul \ (X \). dacă pentru orice \ (x_1, x_2 \ în X \). astfel încât \ (x_1
\ (\ blacktriangleright \) Funcția \ (f (x) \) se numește descrescătoare în intervalul \ (X \). dacă pentru orice \ (x_1, x_2 \ în X \). astfel încât \ (x_1

Funcția se numește nonincreasing pe intervalul \ (X \). dacă pentru orice \ (x_1, x_2 \ în X \). astfel încât \ (x_1
\ (\ blacktriangleright \) Funcțiile ascendente și descrescătoare sunt numite strict monotonice. și non-în creștere și non-descrescătoare - doar monotone.
\ (\ blacktriangleright \) Proprietăți principale:
I. Dacă funcția \ (f (x) \) este strict monotonă pe \ (X \). atunci egalitatea \ (x_1 = x_2 \) (\ (x_1, x_2 \ în X \)) implică \ (f (x_1) = f (x_2) \). și invers.
Exemplu: funcția \ (f (x) = \ sqrt x \) este strict în creștere pentru toate \ (x \ în [0; + \ infty) \). prin urmare, egalitatea \ (\ sqrt x = \ sqrt 4 \) implică \ (x = 4 \).
II. Dacă funcția \ (f (x) \) este strict monotonă pe \ (X \). apoi ecuația \ (f (x) = c1). unde \ (c \) este un număr, are întotdeauna cel mult o soluție pe \ (X \).
Exemplu: funcția \ (f (x) = x ^ 2 \) este strict descrescătoare pentru toate \ (x \ in (- \ infty; 0] \) nu mai mult de o soluție, sau mai degrabă una: \ (x = -3 \).
funcția \ (f (x) = - \ dfrac 1 \) este în creștere strict pentru toate \ (x \ in (-1; + \ infty) \). prin urmare, ecuația \ (- \ dfrac 1 = 0 \) are în acest interval nu mai mult de o soluție, sau mai precis nici una, deoarece. numerotatorul din partea stângă nu poate fi niciodată zero.
III. Dacă funcția \ (f (x) \) nu se micșorează (nu se micșorează) și continuă în intervalul \ ([a, b] \). iar la capetele intervalului ia valori \ (f (a) = A, f (b) = B \). atunci pentru \ (C \ în [A; B] \) (\ (C \ în [B; A] \)) ecuația \ (f (x) = C \) are întotdeauna cel puțin o soluție.
Exemplu: funcția \ (f (x) = x ^ 3 \) este strict în creștere (adică, strict monotonă) și continuă pentru toate \ (x \ in \ mathbb \). cu toate acestea, pentru orice \ (C \ in (- \ infty; + \ infty) \) ecuația \ (x ^ 3 = C \) are exact o soluție: \ (x = \ sqrt [3] \).
Transferăm toți termenii care conțin \ (ax \). stânga și conținând \ (x ^ 2 \) - spre dreapta și luați în considerare funcția
\ f (t) = 5 (t-2) ^ 3 + 15e ^ t + 6e ^ t \ cdot \ sin + 3e ^ t \ cdot \ cos \
Apoi ecuația inițială ia forma:
\ [f (ax) = f (x ^ 2) \]
Să găsim derivatul:
\ f (t) = 15 (t-2) ^ 2 + 15e ^ t \ cdot (1+ cos) \]
pentru că \ (t-2) ^ 2 \ geqslant 0, \ e ^ t> 0, \ 1 + \ cos \ geqslant 0 \). atunci \ (f '(t) \ geqslant 0 \) pentru orice \ (t \ in \ mathbb \).
În plus, \ (f '(t) = 0 \). dacă \ ((t-2) ^ 2 = 0 \) și \ (1 + \ cos = 0 \) în același timp, ceea ce nu se păstrează pentru niciun \ (t \). În consecință, \ (f '(t)> 0 \) pentru orice \ (t \ in \ mathbb \).
Astfel, funcția \ (f (t) \) crește strict pentru toate \ (t \ in \ mathbb \).
Prin urmare, ecuația \ (f (ax) = f (x ^ 2) \) este echivalentă cu ecuația \ (ax = x ^ 2).
Ecuația \ (x ^ 2-ax = 0 \) pentru \ (a = 0 \) are o rădăcină \ (x = 0 \). și pentru \ (a \ ne 0 \) are două rădăcini distincte \ (x_1 = 0 \) și \ (x_2 = a \).
Prin urmare, răspunsul este: \ (a \ in (- \ infty; 0) \ cup (0; + \ infty) \).
Nivel de asociere: Raven EGE
Găsiți toate valorile parametrului \ (a \). pentru fiecare dintre care ecuația \ [2 ^> \ cdot \ log _ >> + \ log_9 + 2)> = 0 \]
are o soluție unică.
Adăugați o atribuire favorită
Să considerăm funcția \ (y = 2 ^ t \ cdot \ log _> \) când \ (t \ geqslant 0 \) (ca \ (\ sqrt \ geqslant 0 \)).
\ Derivative (y '= \ stânga (-2 ^ t \ cdot \ log_9 \ dreapta)' = - \ dfrac \ cdot \ stânga (\ ln 2 \ cdot \ ln + \ dfrac \ dreapta) \).
pentru că \ (2 ^ t> 0, \ \ dfrac> 0, \ \ ln> 0 \) pentru toate \ (t \ geqslant 0 \). atunci \ (y '<0\) при всех \(t\geqslant 0\).
În consecință, pentru \ (t \ geqslant 0 \) funcția \ (y \) scade monotonic.
Ecuația poate fi considerată în forma \ (y (t) = y (z) \). unde \ (z = ax, t = \ sqrt \). Din monotonicitatea funcției rezultă că egalitatea este posibilă numai dacă \ (t = z \).
Prin urmare, ecuația este echivalentă cu ecuația: \ (ax = \ sqrt \). care la rândul său este echivalentă cu sistemul: \ [\ a \ begin \ ^ 2x ^ 2-x-1 = 0 \ ax \ geqslant 0 \ end \
Pentru \ (a = 0 \) sistemul are o soluție \ (x = -1 \). care satisface condiția \ (ax \ geqslant 0 \).
Considerăm cazul \ (a \ ne 0 \). Discriminant al primei ecuații a sistemului \ (D = 1 + 4a ^ 2> 0 \) pentru toate \ (a \). În consecință, ecuația are întotdeauna două rădăcini \ (x_1 \) și \ (x_2 \). și sunt de semne diferite (deoarece prin teorema lui Viet \ (x_1 \ cdot x_2 = - \ dfrac<0\) ).
Aceasta înseamnă că pentru \ (a<0\) условию \(ax\geqslant 0\) подходит отрицательный корень, при \(a>0 \) este adecvată o rădăcină pozitivă. În consecință, sistemul are întotdeauna o soluție unică.
Prin urmare, \ (a \ in \ mathbb \).
Luați în considerare funcția \ (f (x) = 2x ^ 3-3x (ax + x-a ^ 2-1) -3a-a ^ 3) pentru unele fix \ (a \). În acest caz, derivatul nostru este: \ (f '(x) = 6x ^ 2-6ax-6x + 3a ^ 2 + 3 = 3 (x2-2ax + a ^ 2 + x ^ 2-2x + xa) ^ 2 + (x-1) ^ 2) \).
Rețineți că \ (f '(x) \ geqslant 0 \) pentru toate valorile lui \ (x \) și \ (a \). unde \ (0 \) este egal numai pentru \ (x = a = 1 \). Dar cu \ (a = 1 \):
\ (f (x) = 6 (x-1) ^ 2 \ rightarrow f (x) = 2 (x-1) ^ 3 \ Rightarrow \ are o rădăcină unică \ (x = 1 \). care nu satisface condiția. Prin urmare, \ (a \) nu poate fi egal cu \ (1 \).
Acest lucru inseamna ca functia \ (f (x) \) creste strict pentru toate \ (a \ ne 1 \), prin urmare ecuatia \ (f (x) = 0 \) poate avea cel mult o radacina. Având în vedere proprietățile funcției cubice, graficul \ (f (x) \) pentru unele fix \ (a \) va arăta astfel:

Aceasta înseamnă că ecuația are o rădăcină în intervalul \ ([- 1; 0] \). trebuie să fie: \ [\ begin f (0) \ geqslant 0 \\ f (-1) \ leqslant 0 \ end \ rightarrow \ începe a (a ^ 2 + 3) \ leqslant 0 \\ (a + 2) (a ^ 2 + a + 4) \ geqslant 0 \ end \ rightarrow \ începe o \ leqslant 0 \\ o \ geqslant -2 \ end \ rightarrow -2 \ leqslant o \ leqslant 0 \]
Astfel, \ (a \ în [-2; 0] \).
Nivel de asociere: Raven EGE
Găsiți toate valorile parametrului \ (a \). pentru fiecare dintre acestea ecuația \ [(sin_2x-5 \ sin x-2a (\ sin x-3) +6) \ cdot (\ sqrt2a + 8x \ sqrt) = 0 \
(Sarcină de la abonați)
Adăugați o atribuire favorită
Ecuația ODZ este: \ (2x-2x ^ 2 \ geqslant 0 \ quad \ Leftrightarrow \ quad x \ în [0; 1] \). Prin urmare, pentru ca ecuația să aibă rădăcini, este necesar ca cel puțin una dintre ecuațiile \ sinx 2x-5 \ sinx-2a (\ sin x-3) + 6 = 0 \ quad >> \ quad \ sqrt2a + 8x \ sqrt = 0 \] a avut o soluție la DSB.
1) Luați în considerare prima ecuație \ [sin ^ 2x-5 \ sin x-2a (\ sin x-3) + 6 = 0 \ quad \ Leftrightarrow \ quad \ \ sin x = 2a + 2 \\ \ sin x = 3 \\ \ end \ end \ right. \ quad \ Leftrightarrow \ quad \ sin x = 2a + 2 \] Această ecuație trebuie să aibă rădăcini pe \ ([0; 1] \). Luați în considerare cercul:
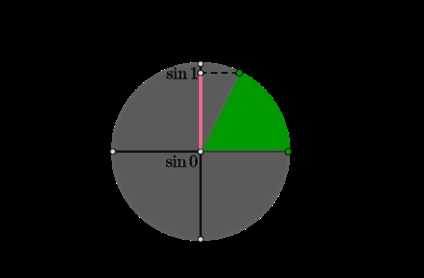
Astfel, vedem că pentru orice \ (2a + 2 \ în [\ sin 0; \ sin 1] \) ecuația va avea o soluție, dar pentru toate celelalte - nu va avea soluții. În consecință, pentru \ (a \ în \ left [-1; -1 + \ sin 1 \ right] \), ecuația are soluții.
2) Luați în considerare a doua ecuație \ [sqrt2a + 8x \ sqrt = 0 \ quad \ Leftrightarrow \ quad 8x \ sqrt = -a \]
Luați în considerare funcția \ (f (x) = 8x \ sqrt \). Derivația derivă: \ [f '(x) = - 4 \ cdot \ dfrac> \] Pe DDZ derivatul are un zero: \ (x = \ frac34 \). care este, de asemenea, un punct maxim al funcției \ (f (x) \).
Rețineți că \ (f (0) = f (1) = 0 \). Aceasta înseamnă că graficul lui \ (f (x) \) este schematic:
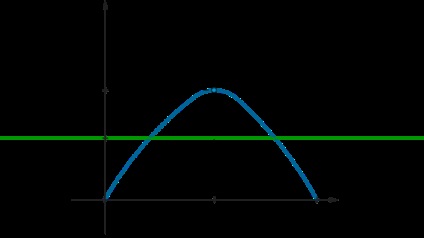
În consecință, pentru ecuația are soluții este necesară programarea \ (f (x) \) intersectează linia \ (y = -a \) (în figură este prezentat un exemplu de realizare adecvat). Adică, trebuie să \ [0 \ leqslant -a \ leqslant f \ left (\ dfrac34 \ dreapta) \ quad \ rightarrow \ quad - \ dfrac2 \ leqslant o \ leqslant 0 \]
3) Astfel, ecuația inițială va avea soluții pentru \ (a \ in \ left [-1; -1+ \ sin 1 \ right] \) sau \ (a \ in \ left [- \ dfrac2; 0 \ right] \). Combinând aceste soluții, obținem \ [a \ in \ left [- \ dfrac2; 0 \ right]. \]
Considerăm familii de funcții \ (f_a (x) = \ sqrt + 5x ^ 2-9x + 3a + 8, \\ g_a (x) = \ dfrac \).
ODZ al ecuației: \ (x \ geqslant 1 \). Pentru aceste \ (x \):
Funcția \ (y_1 = \ sqrt \) este în creștere. Graficul grafic al funcției \ (y_2 = 5x ^ 2-9x \) este o parabolă al cărei vârf este în punctul \ (x = \ dfrac \). În consecință, pentru toate \ (x \ geqslant 1 \), funcția \ (y_2 \) crește, de asemenea, strict (ramura dreaptă a parabolei). pentru că suma funcțiilor strict crescătoare este strict în creștere, atunci \ (f_a (x) \) este strict în creștere (constanta \ (3a + δ \) nu afectează monotonicitatea funcției).
Funcția \ (g_a (x) = \ dfrac \) pentru toate \ (x \ geqslant 1 \) face parte din ramificația dreaptă a hiperboliei și scade strict.
Rezolvarea ecuației \ (f_a (x) = g_a (x) \) - înseamnă găsirea punctelor de intersecție a funcțiilor \ (f \) și \ (g \). Din monotonicitatea lor opusă rezultă că ecuația nu poate avea mai mult de o rădăcină.
Pentru \ (x \ geqslant 1 \) \ (f_a (x) \ geqslant 3a + 4, \ \ \ 0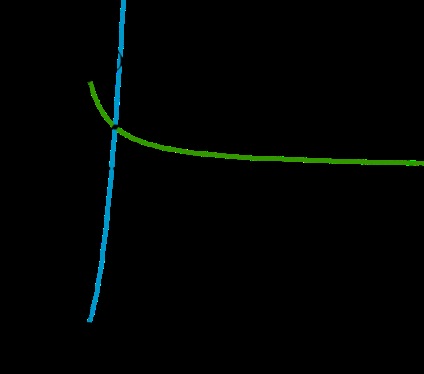
\ [3a + 4 \ leqslant a ^ 2 \ Rightarrow a \ in (- \ infty; -1] \ cup [4; + \ infty)
Trimiteți-le prietenilor: