Curbură a curbei plane. Radius de curbură. Evoluția și evolvarea unei curbe plane


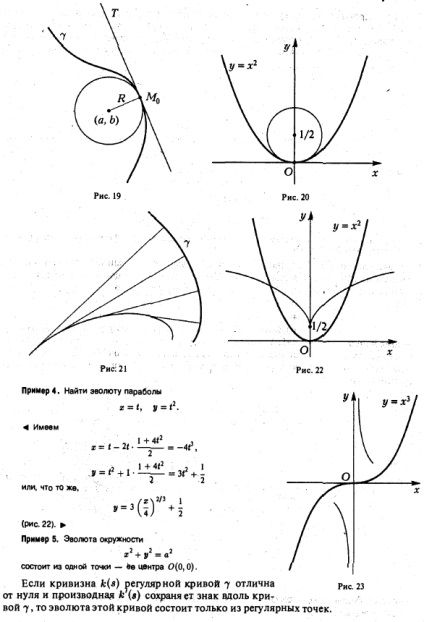





Fie γ o curbă obișnuită și MQ punctul acestei curbe. Definiția. 7 la curbura curbei în punctul M0 este raportul limită atunci când - unghiul dintre tangenta la curba la punctele 7 - ^ M0M lungimea arcului (. Figura 16). Curbura curbei caracterizează rata deviației sale de la tangent. Curbura liniei drepte este zero în fiecare dintre punctele sale. Curbura cercului este constantă și egală cu j, unde a este raza cercului. O curbă obișnuită are o anumită curbură în fiecare dintre punctele sale. Dacă - parametrizare naturală a curbei 7, curbura poate fi găsit prin formula 6 pentru o curbă curbură parameterization plan arbitrar. Radius de curbură. Evoluția curbelor plane și evoluează O cale clară de evoluție a curbelor Spațiale. Cu ajutorul metodelor de referință explicite modul de efectuare a exemplului 1. r1 curbură a parabolei y = 0 la vertexului (0,0) este egal cu 2. Curbura planului de definire a curbei este non-negativ. Cu toate acestea, în multe ^ y4a # v curbura curbei plane este utilă pentru a include un semn. De obicei, selectarea sign-liant vayuts papra ° Niemi tangenta de rotație curba atunci când se deplasează de-a lungul unei curbe cu o creștere a parametrului „4“: curbura este pozitiv dacă tangenta se rotește în sens antiorar (în direcția pozitivă); "-": Curbura curbei este negativă dacă tangenta se rotește în sens orar (în direcția negativă) (Figura 17). shsdosrmvie pentru a stabili în mod explicit curba clorhidric calculată prin „Prmir 2. Curbura sinusoiAy y = sin pozitiv telnv g (egal cu 1) * e vtoch J, -l) și negativ (egal cu -1) tochiv l) (Fig. 18). La punctul Irianien, sinusajul este zero. Dacă curbura curbei în punctul Mo (xo) este diferit de zero, curbura nativă determinată a curbei în acest moment pe cercul de rază R (a), care trece prin punctul Afb (fo), care are în acest moment cu curba 7 ob- rns.18 tangentă Shui și minciuna th sudoare aceeași parte a acestei tangente ca curba 7, eu numesc cercul osculating la punctul curbei 7 AFO, sau un cerc de curbura (Fig. 19). Este clar că curburile curbei și cercul ei de curbură coincid la punctul lor comun. Centrul cercului înconjurător se numește centrul curburii curbei în punctul Af0. Coordonatele sale a și b se calculează cu formulele • Exemplul 3. Pentru parabolei y = x2 la apex 0 (0.0) avem I »j, s = 0. Prin urmare, circumferința curburii parabolei în punctul O poate fi dată de urateg (figura 20). Evoluția unei curbe plane obișnuite este numită setul de centru al acesteia în curbură (Figura 21). Ecuațiile curba 7 înfășurătoare definite parametric sunt următoarele: Găsiți parabole înfășurătoare Exemplul 5. înfășurătoare circumferențială este un singur punct - centrul său 0 (0,0). Dacă curbura curbei regulate 7 este nenulă și un derivat al (e) a salva un semn de-a lungul curbei 7, înfășurătoare acestei curbe constă doar din puncte regulate. Dacă k (e) curbura curbei regulate 7 este zero, la o anumită curbă punct, k (deci) = 0, și derivatul său păstrează semn de-a lungul curbei 7, înfășurătoare curbei se imparte in doua curbe regulate sunt părți înfășurătoare ale curbei 7 când s Fiecare din aceste ramuri se duce la infinit ca s -> sq. Un exemplu în. Curbura parabolei y = x2 0 la vertexului (0,0) este diferit de zero, iar derivatul de curbură 2 nu reține semnul de-a lungul parabolei. De aceea, evolutul parabolei are o singularitate - un punct de întoarcere de primul fel (vezi Figura 22). Exemplul 7. Curbura unei parabole cubice y = x3 Curbura unei curbe plane. Radius de curbură. Evoluția curbelor plane și evoluează O cale clară de evoluție a curbelor Spațiale. Metodele de specificare pentru x = 0 dispar și derivatul său păstrează semnul în apropierea punctului 0 (0,0). De aceea, evoluția unei parabole cubice se împarte în două ramuri obișnuite (figura 23). / Curba involutară γ este o curbă pentru care curba dată γ este evolută. 7 curba evolventă este mulțimea tuturor segmentelor de linie tangentă la curba 7 în așteptare de la punctele de atingere, lungimile de care scad cu o valoare egală cu creșterea arcului curbei 7. O metodă ilustrativ de formare evolvente Postpone la iroizvolnoy din Mo curba 7 punct lungimea curbei arcului. Denumim al doilea capăt al arcului de Af. Acum arătăm că un fir flexibil inextensibil este atașat arcului, un capăt al căruia este fixat la punctul mq. Când firele tensionate sunt rebobinate din curba 7 (din șablon), al doilea capăt M va descrie contravaloarea curbei 7 (Figura 24). unde c este o constantă arbitrară. Astfel, pentru orice curbă obișnuită există un număr infinit de evoluează. Exemplul 8. Evoluția unui cerc este descrisă de ecuațiile formei în care c este parametrul familiei evolvent (Figura 25). § 3. Curbe spațiale. Metode de specificare pe. Parametrică curba spațială predeterminată este un set de 7 puncte M, coordonatele x, y și z sunt definite de relațiile în care - funcțiile sunt continue pe intervalul [a, b), sau, în formă vectorială r, unde curba vizual predeterminată parametrically poate fi kaksled se deplasează punctul M cu coordonate. Exemplul 1. Ecuația "dow" a limitei elicoidale itco * (figura 27). Punctele A și A ale curbei 7 Corespunzând valorilor t = a și t = 6 ale parametrului, respectiv se numesc punctele inițiale și finale ale curbei y. Se spune că o curbă 7 este închisă dacă aceste puncte coincid. Concepte netede și regulate curba spațială introdusă în deplină conformitate cu cazul plat: curba 7, ecuația vectorului parametric predeterminat s este numit n-regulat dacă 1) funcția vectorului g (() este în intervalul [a, b) Derivați continue de ordinul n + 2 ) viteza curbei este pozitivă în fiecare punct. Un alt mod comun de a defini o curbă spațială este modul implicit de definire a curbei ca un set de puncte M, coordonatele x, y și z care sunt soluții ale sistemului de ecuații în care funcția) în anumite condiții. Precizăm important caz special, cel mai frecvent întâlnite în practică: z) sunt funcțiile netede și argumentele lor, la un moment dat următoarele condiții: curbă spațială predeterminată, fiecare implicit punct din care prima condiție (3) este regulat. Exemplul 2. Criminalitatea, viermii mdamsha * vor fi obișnuiți (figura 28). Această crimă reprezintă un cerc mare - "sfera" sferei - de către avionul care dirijează centrul său. Fie γ o curbă regulată definită parametric. Notăm curba punctul Mo 7 care corespunde valorii parametrului, și prin M - punct al curbei care corespunde valorii t unui cartier * o „Direct MQT numit tangenta la curba 7 la punctul Mo, în cazul în care M -“ Mo cel mai mic unghi SA între Această linie dreaptă și linia dreaptă variabilă M0M Fig. 2s tinde la zero. Curba regulată are o tangență la fiecare dintre punctele sale. Vectorul vitezei curbei în punctul M0 este colinar cu tangenta sa în acest punct. Ecuațiile tangent la 7 punctul Mo (®E „Vo“ a) au forma următoare Orice linie care trece prin punctul u la perpendiculara pe tangenta curbei 7 din punctul M0 se numește curba normală la punctul 7 Mo Plan / M0 care trece prin punctele curbei 7 MoT perpendicular tangente la acest moment, a numit planul normal al curbei în punctul Mo (fig. 29). Curba plan normal Ecuația definită parametric, este după cum urmează: Este clar că toate Mo în punctul de curba normală situată în planul său normal de la acest punct. Exemplul 3. Planurile tangente și normale ale helixului la punctul t, (pentru t = j) sunt descrise prin ecuațiile respective. Curba spațială obișnuită este rectificabilă. Lungimea curbei date de ecuația vectorului se calculează prin formula În cazul unei alocări de coordonate a curbei curbei unei curbe plane. Radius de curbură. Evoluția curbelor plane și evoluează O cale clară de evoluție a curbelor Spațiale. Metodele de stabilire a valorii funcției sunt egale cu lungimea arcului curbei 7, închis între punctele A (a) și M (t) (Figura 30). Această funcție crește strict pe intervalul [a, b] și, prin urmare, lungimea arcului poate fi luată ca nou parametru pe curbă. Parametrizarea curbei, unde lungimea arcului s este luată ca parametru, se numește parametrizare naturală. O curbă cu parametrizare naturală are o viteză unitară (cu privire la această parametrizare). Pentru parametrizarea curbei naturale a fost necesară și suficientă pentru a satisface condiția, sau ceea ce este același lucru, Exemplul 4. helix au, prin urmare, o spirală parametrizare naturală poate fi scrisă ca
Articole similare
Trimiteți-le prietenilor: