Cele mai vechi concepte în dezvoltarea geometriei lumii sunt conceptele zonelor multor figuri rectilinie, incluzând: un dreptunghi, o paralelogramă, un triunghi și un trapez. Chiar și în secolul al VII-lea î.H., pătratul dreptunghiului a fost capabil să calculeze egiptenii. Au înmulțit lungimea cu lățimea.
Aritmetica și algebra babiloniene, de asemenea, au fost suficient de dezvoltate, după cum reiese din tabletele cuneiforme găsite în timpul săpăturilor. Geometria babiloniană a avut o idee despre proporționalitatea segmentelor care intersectau liniile paralele, precum și despre teorema lui Pitagora și chiar despre calculul volumelor și zonelor unor figuri. În același timp, babilonienii au luat obiecte concrete din viața de zi cu zi sub figurile spațiale. De exemplu, în construcția de clădiri circulare, au circumscris aproximativ circumferința celor trei diametre. Zona dreptunghiului a fost calculată prin numărul de pași trecuți. Aparent pentru acea vreme asemenea definiții ale semnificațiilor erau destul de acceptabile. O astfel de geometrie aplicată a fost caracteristică multor popoare ale lumii și a fost folosită pe scară largă în rezolvarea diferitelor probleme interne.
Un învățat remarcabil al timpului său, Archimedes, dovedind teoreme pe pătrate de figuri, a folosit metoda epuizării. De fapt, aceasta nu este altceva decât o dovadă indirectă, care pornește de la contrariul. Ideea principală a metodei lui Archimedes este că, în interiorul figurii, a cărei zonă o căutați, este necesar să introduceți cifrele corecte. Folosind variante ale metodei de epuizare, un om de știință remarcabil a reușit să dovedească multe teorii.
Teorema: zona dreptunghiului este egală cu produsul laturilor sale adiacente.
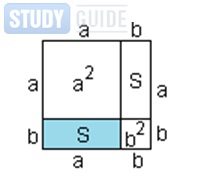
Transformați dreptunghiul nostru într-un pătrat. Pentru a face acest lucru, creștem partea lui b la lungimea laterală a
Ca rezultat, avem patru pătrate. Știm că pătratul pieței este (a + b) 2. În același timp, aceste pătrate sunt alcătuite din două dreptunghiuri: un dreptunghi cu suprafața S și același dreptunghi cu aceeași zonă, precum și două pătrate cu zone a 2 și b 2. Plecând de la faptul că patrulaterul nostru constă nu dintr-un patrulater, ci din mai multe, suprafața sa va fi egală cu suma tuturor zonelor acestor patrulaterale. Acest lucru iese din proprietatea piețelor:
(a + b) 2 = S + S + a 2 + b 2 sau 2 + 2ab + b 2 = 2S + a 2 + b 2.
Și aceasta înseamnă că S = ab. Aceasta înseamnă că teorema noastră este dovedită.
Articole similare
-
Grădina Anichkov Palace în zona de pe insula din Sankt Petersburg
-
Cum să găsim zona paralelogramului - o formulă prin diagonale
Trimiteți-le prietenilor: