Valori aproximative ale numerelor reale
Și în clasele a VII-a și a VIII-a am rezolvat grafic ecuațiile. Ați observat că în aproape toate aceste exemple ecuațiile au rădăcini "bune"? Acestea erau numere întregi, care au fost găsite cu ușurință folosind grafice, în special pe hârtie în carouri. Dar acest lucru nu este întotdeauna cazul, dar încă am selectat exemple "bune".
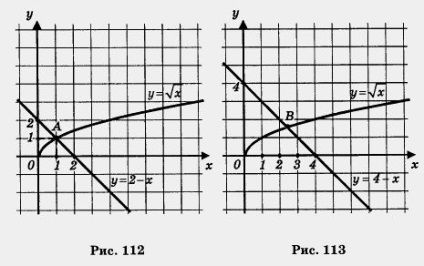
Luați în considerare două ecuații: = 2 - x și = 4 - x. Prima ecuație are o rădăcină unică x = 1, deoarece graficele funcțiilor y = și y = 2 - x se intersectează la același punct A (1; 1) (Figura 112). În cel de-al doilea caz, graficele funcțiilor - fc și y = 4 - x se intersectează la un punct B (Figura 113), dar cu coordonate "rele". Folosind desenul, putem concluziona că abscisa punctului B este aproximativ egală cu 2,5. În astfel de cazuri nu vorbim despre soluția exactă, ci despre soluția aproximativă a ecuației și scrieți aceasta:
Acesta este unul dintre motivele pentru care matematicienii au decis să introducă noțiunea unei valori aproximative a unui număr real. Există un al doilea motiv și poate chiar mai important. Ce este un număr real? Aceasta este o fracțiune zecimală infinită. Dar pentru a face calcule cu fracții zecimale infinite este incomod, deci în practică folosiți valori aproximative ale numerelor reale. De exemplu, pentru un număr, utilizați egalitatea aproximativă 3.141 sau 3.142. Prima se numește valoarea aproximativă (sau aproximarea) numărului n printr-un defect cu o precizie de 0,001; Cel de-al doilea se numește valoarea aproximativă (aproximare) a numărului k peste excesul de până la 0,001. Este posibil să se ia aproximări mai exacte: de exemplu, 3.1415 - aproximarea cu un defect cu o precizie de 0.0001; 3.1416 - aproximare în exces cu o precizie de 0,0001. Putem lua aproximații mai puțin precise, să zicem, cu o precizie de 0,01: pentru un deficit de 3,14, pentru un exces de 3,15.
Semnul egalității aproximative "pe care l-ați folosit în cursul matematicii clasei 5-6 și probabil în cursul fizicii și am folosit-o înainte, de exemplu în §27.
Exemplul 1. Găsiți valori aproximative pentru deficiență și pentru exces cu o precizie de 0,01 pentru numere:
a) Știm că = 2.236. (a se vedea § 27), prin urmare, 2.23 este o aproximare printr-un defect cu o precizie de 0,01; 2.24 este o aproximare în exces cu o precizie de 0,01.
b) 2 + = 2.000. + 2,236. = 4,236. Prin urmare, 2 + 4,23 este o aproximare printr-un defect cu o precizie de 0,01; 2 + 4,24 este o aproximare în exces cu o precizie de 0,01.
c) Avem 0.31818. (vezi secțiunea 26). Astfel, 0,31 este o aproximare printr-un defect cu o precizie de 0,01; 0,32 este o aproximație în exces cu o precizie de 0,01.
Aproximarea de către o deficiență și aproximarea prin exces sunt uneori numite numere naturale.
Definiția. Eroarea de aproximare (eroarea absolută) este modulul diferenței dintre valoarea exactă a lui x și valoarea sa aproximativă a: eroarea de aproximare este | x - a |.
De exemplu, eroarea de egalitate aproximativă este exprimată ca sau, respectiv,
Se pune o întrebare pur practică: care este cea mai bună aproximare, lipsă sau exces, adică, în ce caz este eroarea mai mică? Acest lucru, desigur, depinde de numărul specific pentru care se fac aproximări. De obicei, atunci când rotunzi numere pozitive, utilizați următoarea regulă:

Aplicăm această regulă pentru toate numerele considerate în această secțiune; alegem pentru numerele considerate aproximările pentru care eroarea este cea mai mică.
1) = 3,141592. Cu o precizie de 0.001, avem 3.142; aici prima cifră aruncată este de 5 (pe locul patru după punct zecimal), astfel încât au luat o aproximare a excesului.
Până la 0,0001 3,1416, avem - și aici abordarea adoptată de excesul, astfel cum exprimate de prima cifră (pe locul al cincilea, după punctul zecimal) este 9. Dar, cu o precizie de 0,01 trebuie să ia în abordarea lipsei de: 3.14.
2) = 2,236. Cu o precizie de 0,01, avem 2,24 (aproximație peste exces).
3) 2 + = 4,236. Cu o precizie de 0,01, avem 2 + 4,24 (aproximarea excesului).
4) = 0,31818. Cu o precizie de 0,001, avem 0,318 (aproximare cu un defect).
Să luăm în considerare ultimul exemplu în detaliu. Luați fragmentul mărit al liniei de coordonate (Figura 114).
Punctul aparține segmentului [0.318, 0.319], prin urmare distanțele sale de la capetele segmentului nu depășesc lungimea segmentului. Distanțele punctului de la capetele segmentului sunt egale cu, respectiv, intervalul [0.318, 0.319] egal cu 0.001. Prin urmare, u
Deci, în ambele cazuri (și pentru a aproxima numărul printr-un defect, și pentru a aproxima cu exces), eroarea nu depășește 0,001.
Până acum am spus: aproximări cu o precizie de 0,01, până la 0,001, etc. Acum putem pune lucrurile în ordine în utilizarea terminologiei.
Dacă a este o valoare aproximativă a numărului x și. să spunem că eroarea de aproximare nu depășește h sau că numărul x este egal cu numărul a până la h.
De ce este important să găsiți valori aproximative ale numerelor? Faptul este că este practic imposibil să operați cu zecimale infinite și să le folosiți pentru a măsura cantitățile. În practică, în multe cazuri, în loc de valori exacte, aproximările sunt luate cu o precizie predeterminată (eroare). Această idee este încorporată și calculatoare, care sunt afișate pe display decimal finite, t. E. Aproximarea afișat pe ecranul (rare excepții, când numărul afișat este fracția zecimală finală, se poate potrivi pe ecran).
Colecție de note de lecții în matematică descărcare. planificare tematică calendaristică, manuale în toate disciplinele online
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.
Articole similare
Trimiteți-le prietenilor: