a) ((A B) (C A)) (B C);
b) ((((A B) A) B) C) C;
c) (A (B C)) (A C) (A B)).
2. Să aducă formulele SDNF și SKNF:
3. Pentru un anumit set de valori de variabile, construiți o conjuncție elementară care este adevărată numai pentru acest set de valori ale variabilelor.
4. Pentru un anumit set de valori ale variabilelor, construiți o disjuncție elementară care este falsă numai pentru acest set de valori ale variabilelor.
5. Construiți SKNF și SDNF, echivalente cu această formulă, și găsiți interpretări pe care formula este adevărată și falsă:
6. Pentru funcțiile g și h, definite în Tabelul 1, găsiți formele SKN și VOS și cele mai simple formule care realizează aceste funcții.
7. Creați două funcții Boolean care planifică un aderent binar pe 1 biți conform tabelului următor
unde x1 și x2 sunt aceleași cifre ale sumelor 1 și 2; e1 este unitatea de transport de la cea mai puțin semnificativă cifră; e2 - unitatea de transfer la cea mai mare cifră a sumei; este rezultatul sumării.
8. Construiți o formulă din trei variabile, care este adevărată dacă și numai dacă exact două variabile sunt false.
9. Construiește o formulă din trei variabile, care ia aceeași valoare ca majoritatea (minoritatea) variabilelor.
10. Conform SKNF cu formula U, construiți:
a) CDNF a formulei duble U *;
b) SKNF cu formula U;
c) CDNF cu formula U.
11. Conform SDNF, formulele U și CDNF cu formula B sunt:
a) formulele SNNF și SDNF (U B);
b) SNNF și SDNF cu formula (U B);
c) SKNF și SDNF cu formula (U B).
3. Sisteme complete de operare
Se spune că sistemul de operații este complet. dacă orice operație logică poate fi reprezentată de o formulă de peste .
Deoarece fiecare formulă poate fi reprezentată de formula redusă, sistemul 0 = = este complet.
Sistemul reduce la *. este marcat cu *. Dacă toate operațiunile sistemului * sunt reprezentabile prin formule pe sistem . Dacă * este completă, atunci este completă.
Ultima afirmație oferă una dintre modalitățile de a demonstra completitudinea sistemului de operațiuni - reducerea acestuia la un sistem complet cunoscut, de exemplu, la 0. Asta este, sistemul este complet, prin operațiile căruia se poate exprima o conjuncție, o disjuncție și o negare.
Sarcină. Dovedește caracterul complet al sistemului 5 =.
Soluția. Reducem sistemul 5 la sistemul complet 0.
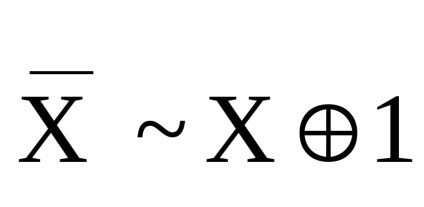
.
Dacă o formulă arbitrară Zhegalkin algebra, realizând o funcție booleană f, deschide parantezele și să facă toate simplificări posibile, vom obține o formulă având forma unei sume de produse, care este un polinom de mod 2. Această formulă se numește Zhegalkin polinomul pentru această funcție. Se numește o funcție liniară, care este liniar polinomială Zhegalkin.
Sarcină. Prezintă formula (x1 x2) (
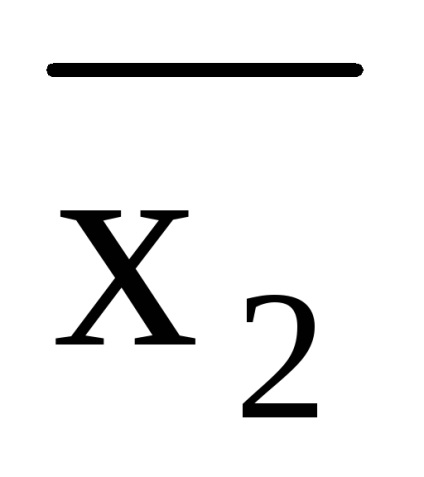
(x1 x2) (
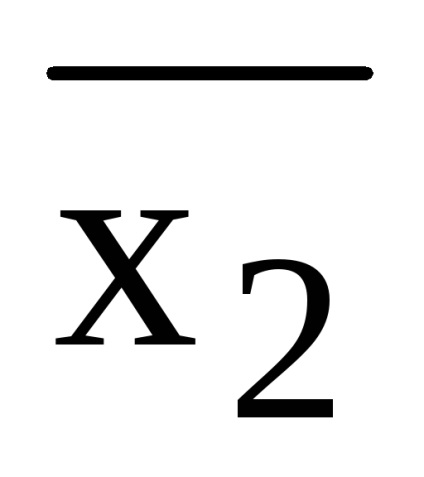
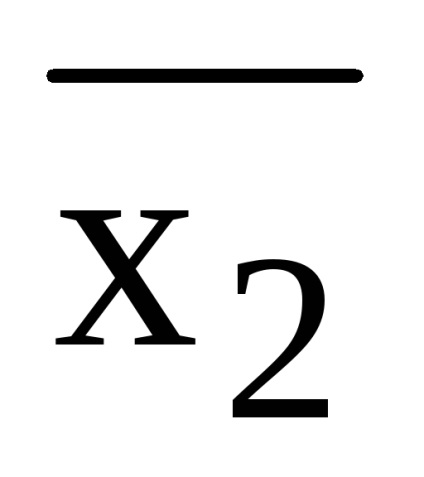
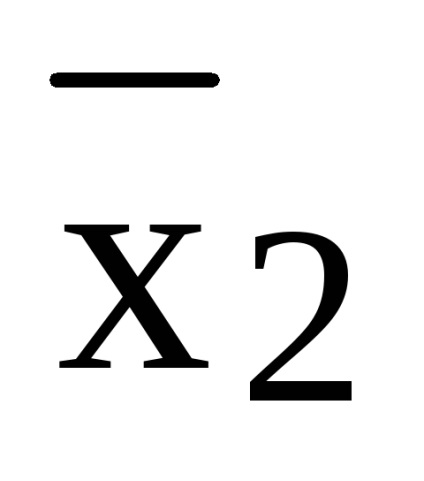
= x1 x2 x3 x x1
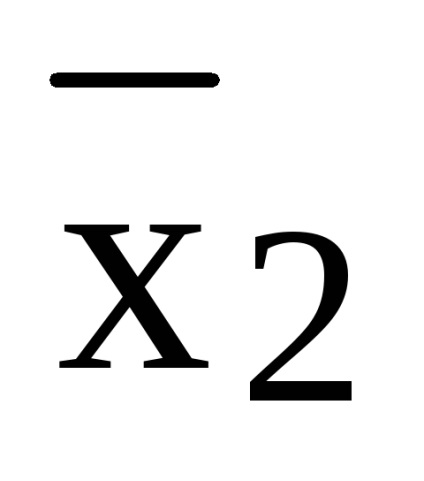
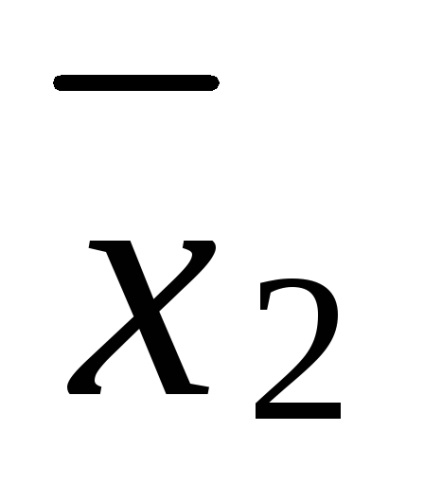
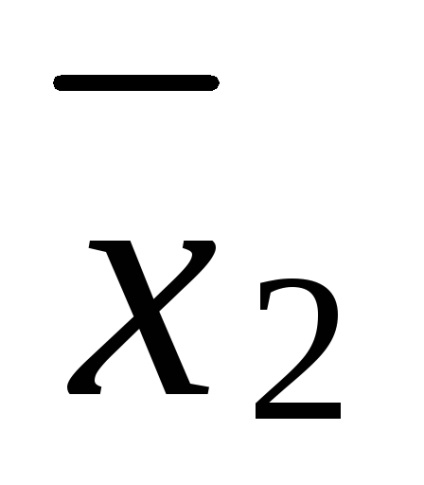
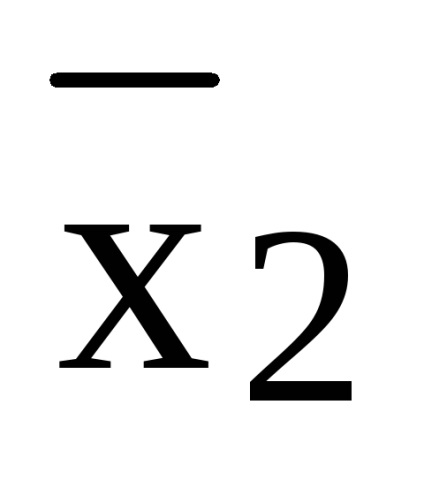
Polinomul rezultat nu este liniar și are gradul 3.
Reducerea la un sistem complet de operațiuni este o condiție necesară pentru completitudinea sistemului de operațiuni. O condiție necesară și suficientă pentru completitudinea unui sistem de operare este formulată în termeni de funcții booleene.
Un sistem de funcții booleene F se spune că este complet dacă orice funcție poate fi realizată printr-o formulă peste F.
Teorema postului. Sistemul boolean de funcții este completă dacă și numai dacă conține cel puțin o funcție, nu salvați 0, cel puțin o funcție, nu salvați 1, cel puțin o funcție nesamodvoystvennuyu, cel puțin o funcție non-monotone și cel puțin o funcție non-lineară.
Sarcină. Demonstrați caracterul complet al sistemului 0. utilizând condiția necesară și suficientă de completare.
Soluția. Considerăm sistemul corespunzător al funcțiilor Boolean F0 =
Clasă de funcții care păstrează 0.
Clasa de funcții care păstrează 1.
Articole similare
Trimiteți-le prietenilor: