In teoria grafurilor, adâncimea arborelui unui grafic neorientat conectat G - este un invariant numeric de G. înălțime minimă de copac Tremaux [en] pentru supergraphs graf G. Aceste concepte invariante și similare se găsesc sub diferite denumiri în literatura de specialitate, inclusiv numărul de topuri de rang comandat numărul cromatic și înălțimea minimă excludeți arborele. Conceptul este, de asemenea, aproape de concepte, cum ar fi rang ciclic [en] direcționat grafice și înălțimea de iterație regulate limba limbi [1]. Intuitiv, în cazul în care lățimea măsurilor grafic de arbori cum graficul este departe de copac, măsurile de adâncime de copac modul în care graficul este departe de steaua.
Adâncimea arborelui grafului G poate fi definită ca înălțimea minimă a pădurii F cu proprietatea că orice margine a graficului G conectează o pereche de vârfuri legate de relația strămoș-copil în F [2]. Dacă G este conectat, această pădure ar trebui să fie singurul copac. Pădurea nu trebuie să fie o subgrafă a graficului G, dar dacă este, atunci acesta este arborele Tremo [pentru] G.
Setul de perechi de copii strămoși în F formează un grafic trivial perfect [ro]. iar înălțimea F este dimensiunea celei mai mari clicuri a acestui grafic. Astfel, adâncimea copacului poate fi alternativ definită ca dimensiunea celei mai mari clicuri în supergraful trivial perfect al graficului G. Aceasta este o imagine oglindă a lățimii arborilor. care este una mai mică decât dimensiunea celei mai mari clicuri din supergraful chordal al graficului G [3]
O altă definiție este următoarea:
unde V este setul de vârfuri ale graficului G și G i sunt componentele conectate ale G [4]. Această definiție reflectă definiția rangului ciclic al grafurilor orientate spre [en], care utilizează conectivitate strictă și componente strict legate, în loc de conectivitate nedirecționată și componente conectate.
Adâncimea copacului poate fi determinată utilizând culoarea grafurilor. Culoarea centrată a unui grafic este o culoare de vârf care are proprietatea că în orice subgraf generat conectat există o culoare care apare exact o dată. Apoi adâncimea arborelui este dimensiunea minimă a culorilor necesare pentru colorarea centrat a graficului. Dacă F este o pădure cu o înălțime d. având proprietatea că orice margine graficului G conectează strămoș și arbore descendent, este posibil să se obțină colorarea graficului Gd flori centrate prin colorare fiecare vârf de culoare, cu un număr, egală cu distanța de la rădăcina graficului F [5].
În cele din urmă, o puteți defini în termeni de joc fictiv [en]. Mai exact, la fel ca jocul "hoți de poliție" [en]. Reprezentăm următorul joc pe un grafic nedirecționat. Sunt doi jucători, un tâlhar și un polițist. Robul are un cip, pe care îl mișcă de-a lungul marginilor graficului. Un polițist are un număr nelimitat de jetoane, dar vrea să minimizeze numărul de jetoane folosite. Un polițist nu-și poate mișca jetoanele, plasat pe grafic. Jocul este după cum urmează. Robotul își plasează cipul, apoi ofițerul de poliție spune unde dorește să pună următorul cip, iar tâlharul își poate muta cipul de-a lungul marginilor, dar nu prin vârfurile ocupate. Jocul se termină atunci când polițistul plasează următorul cip deasupra cipului de luptă. Adâncimea arborelui acestui grafic determină numărul minim de jetoane necesare pentru câștigul garantat [6] [7]. Pentru stele, doar două cipuri sunt suficiente - plasăm primul cip în centrul stelei, forțând hoțul să meargă în raze și apoi plasați cel de-al doilea cip pe cipul tâlharului. Pentru o cale cu n noduri, polițistul folosește o strategie binară de căutare. care garantează utilizarea a nu mai mult de jetoane ⌈ log 2 (n + 1) ⌉ (n + 1) \ rceil>.
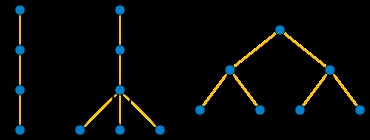
Adâncimea graficului complet al arborelui este egal cu numărul de noduri, și în acest caz, singura posibilă pădure F. astfel încât fiecare pereche de noduri trebuie să fie în relațiile părinte-copil, o singură cale. În mod similar, adâncimea arborelui completează graficul bipartit Kx, y este egal cu min (x, y) + 1, ca și cum nu am avea vârfuri, păduri frunze F trebuie să aibă cel puțin min (x, y) de strămoși în F. Wood, unde min atins (x, y) + 1 poate fi construit prin formarea calea nodurilor o proporție mai mică din grafic și nodurile formează o proporție mai mare de copac frunze F. conectat la calea apex de jos.
Adâncimea arborelui cu noduri n este exact ⌈ log 2 (n + 1) ⌉ (n + 1) \ rceil>. Pădurea F. reprezentând această cale cu o asemenea adâncime poate fi formată prin plasarea rădăcinii în punctul intermediar al căii F și continuarea recursiunii în două căi mai mici pe ambele părți ale rădăcinii [8].
Adâncimea copacilor și legătura cu lățimea copacului
Orice pădure cu n noduri are o adâncime a copacului de O (log n). Pentru pădure, puteți găsi întotdeauna un număr constant de vârfuri, a căror îndepărtare dă pădurea, care poate fi împărțită în două sub-păduri mai mici, cu câte 2 n / 3 vârfuri maxim. Prin împărțirea recursivă a acestor două sub-păduri, este ușor să se atingă o limită superioară logaritmică a adâncimii copacilor. Aceeași tehnică aplicată la descompunerea arborelui de grafic arată că dacă lățimea arborelui grafului n-vertex G este egală cu t. atunci adâncimea arborelui graficului G este O (t log n). [9] Deoarece graficele externe sunt grafice. paralele-grafice consecutive și grafice ale Halin au o lățime limitată de copaci, toate au, de asemenea, o adâncime logaritmică maximă de copaci.
În cealaltă direcție, lățimea arborelui grafului nu depășește adâncimea arborelui. Mai precis, lățimea arborelui nu depășește lățimea traseului [en]. care este de maxim unu mai mică decât adâncimea copacului [10] [11].
Minorul lui G este un alt grafic format din subgraful lui G prin contractarea unor margini. Adâncimea copacului este monotonă la minori - orice minor al graficului G are o adâncime a copacului care nu depășește adâncimea arborelui grafului G însuși [12]. Astfel, prin teorema lui Robertson-Seymour, pentru orice fix d setul de grafuri cu adâncimea unui copac nu depășește d. are un număr finit de minori interzise.
Dacă C este clasa grafurilor închise în ceea ce privește formarea minorilor, atunci graficele din C au o adâncime de copac O (1) dacă și numai dacă C nu include toate căile [13].
Adâncimea lemnului are o strânsă legătură cu teoria subgrafurilor generate de grafic. În clasa grafurilor cu adâncimea copacilor nu mai mult de d (pentru orice d natural fix), proprietatea de a fi generată de un subgraf este complet cvasi-ordonată [en] [14]. Ideea de bază a dovezii că această legătură este complet cvasi-ordonată este de a folosi inducția pe d. Pădurile de înălțime d pot fi interpretate ca o secvență de schele de înălțime d-1 (formată prin îndepărtarea rădăcinilor copacilor cu înălțimea d), iar lema Higman poate fi folosită. pentru a arăta că aceste secvențe sunt complet cvasi-ordonate.
Din destul de cvasi rezultă că orice proprietate a graficului, născut monotonă de subgrafurilor, este generat de un număr finit de subgrafurilor interzise, și, prin urmare, pot fi verificate în timp polinomial pentru graficele cu adâncime limitată de lemn. Grafice cu adâncime copac care nu depășește d. ei înșiși au un număr finit de subgrafe interzise generate. [15]
Dacă C este o clasă de grafice cu degenerare limitată [en]. graficele dintr-un set C au o lățime de copaci limitată dacă și numai dacă există o cale care nu poate apărea ca un subgraf generat în C [13].
Determinarea adâncimii unui arbore este o sarcină computațională complexă - problema de recunoaștere corespunzătoare este NP-completă [16]. Problema rămâne NP-completă pentru grafice bipartite [17]. precum și pentru graficele chordale [18].
Din momente pozitive - adâncimea copacului poate fi calculată în timp polinomial pentru graficele intervalului [19]. ca și pentru graficele permutării, graficele trapezoidale, graficele de intersecție ale arcurilor circulare, graficele permutării ciclice și graficele de limitare a finiteității dimensiunilor limitate [20]. Pentru arborii non-orientați, adâncimea unui copac poate fi calculată în timp liniar [21] [22].
Bodlender, Gilbert, Hafsteinsson Kloks și [10] a propus un algoritm de căutare de aproximare coeficient adâncimea arborelui de aproximare c O ((log n) 2))>. Algoritmul se bazează pe faptul că adâncimea arborelui depinde logaritmic de lățimea arborelui graficului.
Deoarece adâncimea grafului copac minori monotone, sarcina de căutare fixedly solubil parametrically [en] - există un algoritm pentru calcularea adâncimii unui copac, în timpul f de lucru (d) n O (1)>. unde d este adâncimea graficului dat și n este numărul de vârfuri. Astfel, pentru orice valoare fixă a lui d, testul este de a verifica dacă adâncimea copacului depășește d. poate fi rezolvată în timp polinomial. Mai precis - în dependență de n acest algoritm poate fi liniară prin următoarea metodă: construirea unui arbore de căutare în profunzime și verifica mai mare adâncimea arborelui 2 valoare d sau nu. Dacă mai mult, adâncimea copacului este mai mare decât d și problema este rezolvată. Dacă nu, poate fi folosit pentru a construi căutarea copac, la o adâncime superficială a arborelui de descompunere [en] și tehnică standard de programare dinamică pentru grafice cu lățime arbore mărginit pentru a calcula adâncimea timpului liniar [23].
Puteți calcula adâncimea copacului exact pentru grafice, valoarea adâncimii pentru care poate fi mare, într-un timp O (cn) cu o constantă c. puțin mai puțin de 2. [24]
Articole similare
Trimiteți-le prietenilor: