Din moment ce sinusul și cosinusul nu depind de adăugarea unui unghi multiplu
Iar această egalitate este deja evidentă, deoarece aceasta este forma trigonometrică a unui număr complex.
Astfel, logaritmul există pentru toate punctele din plan, cu excepția zero. Pentru un număr pozitiv real, argumentul este 0, deci acest set infinit de puncte are forma. adică, una dintre valori, și anume când. cade pe axa reală. Dacă calculam logaritmul unui număr negativ, ajungem. adică, mulțimea de puncte este deplasată în sus și nici una dintre ele nu se încadrează pe axa reală.
Se poate observa din formula că doar cu argumentul zero al numărului inițial una dintre valorile logaritmului se încadrează pe axa reală. Și aceasta corespunde semiaxisului corect și de aceea numai logaritmii de numere pozitive au fost luate în considerare în cursul matematicii școlare. De asemenea, există logaritme de numere negative și imaginare, dar nu au nicio valoare pe axa reală.
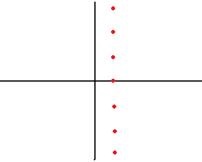
Figura următoare arată unde în plan sunt localizate toate valorile logaritmului unui număr pozitiv. Una dintre ele se află pe axa reală, restul fiind mai mare și inferioară. . și așa mai departe. Pentru un număr negativ sau complex, argumentul este nenul, deci această secvență de vârfuri se deplasează vertical, ca urmare a faptului că nu va exista un singur punct pe axa reală.
Soluția. Definim modulul unui număr (egal cu 2) și al argumentului 180 0. că este. Apoi =.

Anexa 1. Întrebări pentru probe (pentru bilete).
1. Dovediți integrarea prin părți.
1. Dovediți că înlocuirea. unde r = HOC (r1, rk) reduce integral la integrala fracțiunii raționale.
2. Dovada că înlocuirea unui înlocuitor reduce integralitatea formei la integrala unei fracții raționale.
3. Derulați formulele de transformare sinusoidală și cosinus
pentru o substituție trigonometrică universală.
4. Demonstrați faptul că, în cazul în care funcția este ciudată în raport cu cosinusul, înlocuirea reduce integral la o fracție rațională.
5. Dovediți că în cazul în care
înlocuire: reduce integral la o fracție rațională.
6. Demonstrați faptul că pentru un integral al formei, înlocuiți integrale cu fracțiunea rațională.
7. Dovediți formula
8. Dovedeste ca pentru un integral al formei, integrala este inlocuita de o fractiune rationala.
9. Dovedeste ca pentru un integral al formei substitutia reduce integral la o fractiune rationala.
1. Dovediți că funcția este o caracteristică antiderivativă a funcției.
2. Dovediți formula Newton-Leibniz :.
3. Dovediți formula pentru lungimea unei curbe definite explicit:
4. Dovedește o formulă pentru lungimea unei curbe date în coordonate polare
Dovedeste teorema: converge. converge.
1. Derivează (demonstrați) formula pentru zona unei suprafețe definite explicit.
2. Derivarea formulelor pentru trecerea la coordonatele polare.
3. Derivarea determinantului Jacobi al coordonatelor polare.
4. Derivarea formulelor de tranziție la coordonatele cilindrice.
5. Derivarea determinantului Jacobi al coordonatelor cilindrice.
6. Derivarea formulelor pentru trecerea la coordonatele sferice:
1. Dovediți ca înlocuirea să reducă o ecuație omogenă la o ecuație cu variabile de separare.
2. Se deduce forma generală a soluției unei ecuații liniare omogene.
3. Derulați forma generală a soluției unei ecuații liniare neomogene prin metoda Lagrange.
4. Dovada că înlocuirea reduce ecuația lui Bernoulli la o ecuație liniară.
1. Dovediți că substituția reduce ordinea ecuației cu k.
2. Dovada că înlocuirea reduce ordinea ecuației cu una.
3. Dovediți teorema: O funcție este o soluție a unei ecuații diferențiale omogene diferențiale este o rădăcină caracteristică.
4. Dovediți teorema conform căreia o combinație liniară de soluții de difuziune omogenă liniară. ecuația are și soluția sa.
5. Dovediți teorema privind impunerea soluțiilor: Dacă este soluția unei ecuații diferențiale liniare neomogene cu partea dreaptă. a este o soluție a aceleiași ecuații diferențiale, dar cu partea dreaptă. atunci suma este o soluție a ecuației cu partea dreaptă.
1. Dovediți teorema conform căreia sistemul de funcții este dependent de liniar.
2. Dovedește o teoremă asupra existenței n soluțiilor linear independente ale unei ecuații diferențiale omogene de ordin n.
3. Dovedeste ca daca 0 este o radacina a multiplicitatii. atunci sistemul de soluții care corespund acestei rădăcini are forma.
1. Dovediți să utilizați formularul exponențial în care multiplicarea numerelor complexe înmulțește modulele, iar argumentele se adaugă.
2. Dovediți formula Moivre pentru gradul n
3. Dovediți o formulă rădăcină a ordinului n cu un număr complex
4. Dovedeste ca u
sunt generalizări ale sinusului și cosinusului, adică pentru numere reale, aceste formule dau un sinus (cosinus).
5. Dovediți formula logaritmului unui număr complex:
Întrebări mici și orale privind teoria (pentru colocviile).
1. Ce este un integrativ primitiv și nedefinit, care sunt ele diferite?
2. Explicați de ce, de asemenea, este antitetic.
3. Scrieți formula de integrare după părți.
4. Ce fel de înlocuire este necesar în integralitatea speciei și cum elimină rădăcinile?
5. Notați forma de descompunere a integranței fracțiunilor raționale în protozoare în cazul în care toate rădăcinile sunt distincte și reale.
6. Scrieți forma de descompunere a integranței fracțiunilor raționale în protozoare în cazul în care toate rădăcinile sunt reale și există o rădăcină multiplă a multiplicității k.
1. Notați descompunerea unei fracții raționale în fracțiuni mai simple în cazul în care numitorul are un factor de 2 grade cu discriminant negativ.
2. Ce înlocuire reduce integral la o fracție rațională?
3. Ce este substituția trigonometrică universală?
4. Ce substituții se fac în cazurile în care funcția sub semnul integral este ciudată în raport cu sinusul (cosinusul)?
5. Ce substituții se fac în prezența unor expresii în integrad. . sau.
1. Definirea unui integral integrat.
2. Listați câteva dintre proprietățile de bază ale unui integral integrat.
3. Notați formula Newton-Leibniz.
4. Scrieți formula pentru volumul corpului de revoluție.
5. Scrieți o formulă pentru lungimea unei curbe definite explicit.
6. Scrieți o formulă pentru lungimea curbei definite parametric.
1. Definirea integrala necorespunzatoare (prin intermediul unei limite).
2. Ce distinge integralele necorespunzătoare de tipul 1 și 2.
3. Dați exemple simple de integrale convergente de tipul 1 și 2.
4. Pentru ce convergență sunt integralele (T1).
5. Deoarece convergența se referă la limita finită a derivatului antiderivant (T2)
6. Care este semnul necesar al convergenței, formularea acesteia.
7. Semnul de comparație în forma finală
8. Simptom de comparație în forma limitativă.
9. Definirea unui integrat multiplu.
1. Modificați ordinea de integrare, arătați în cel mai simplu exemplu.
2. Scrieți formulele suprafeței.
3. Care sunt coordonatele polare, scrieți formulele de tranziție.
4. Ce este Jacobianul sistemului de coordonate polare?
5. Care sunt coordonatele cilindrice și sferice, care este diferența lor.
6. Care sunt coordonatele cilindrice (sferice)?
1. Ce este o ecuație diferențială a ordinului 1 (forma generală).
2. Ce este o ecuație diferențială a ordinului 1, rezolvată cu privire la derivat. Dați un exemplu.
3. Ce este o ecuație cu variabile separabile.
4. Care este soluția generală, particulară, condițiile Cauchy.
5. Ce este o ecuație omogenă, care este metoda generală pentru rezolvarea ei.
6. Ce este o ecuație liniară, care este algoritmul pentru rezolvarea acesteia, care este metoda Lagrange.
7. Care este ecuația Bernoulli, algoritmul pentru soluția sa.
1. Ce substituție este necesară pentru o ecuație de un fel.
2. Ce substituție este necesară pentru o ecuație de un fel.
3. Arătați prin exemple cum puteți să exprimați în formular.
4. Ce este o ecuație liniară diferențială a ordinului n.
5. Care este polinomul caracteristic, ecuația caracteristică.
6. Formulează o teoremă asupra funcției r pentru care soluția este o ecuație diferențială omogenă liniară.
7. Formulează o teoremă că o combinație liniară de soluții de o ecuație lineară omogenă este, de asemenea, soluția sa.
8. Formulează o teoremă privind impunerea soluțiilor și a corolarilor din aceasta.
9. Ce este un sistem funcțional dependent de funcționalitate liniară și independentă, dați câteva exemple.
10. Care este determinantul sistemului Vronsky al funcțiilor n, dați un exemplu al determinantului Vronsky pentru sistemele LZS și LNS.
1. Care este proprietatea determinantului Wronskian dacă sistemul este dependent de liniar.
2. Câte soluții independente liniar ale unei ecuații diferențiale omogene de ordin n nu există.
3. Definirea FSS (sistemul fundamental de soluții) a unei ecuații liniare omogene de ordine n.
4. Câte funcții sunt incluse în FSR?
5. Scrieți forma sistemului de ecuații pentru găsirea metodei Lagrange pentru n = 2.
6. Notați formularul soluției particulare în cazul în care
7. Ce este un sistem liniar al ecuațiilor diferențiale, scrieți un exemplu.
8. Ce este un sistem autonom de ecuații diferențiale.
9. Sensul fizic al unui sistem de ecuații diferențiale.
10. Scrieți ce funcții are sistemul de ecuații, dacă sunt cunoscute valorile proprii și vectorii proprii ai matricei acestui sistem.
1. Care este unitatea imaginară.
2. Care este numărul de conjugat și ce se va întâmpla când se înmulțește cu numărul inițial.
3. Care este forma trigonometrică, exponențială a unui număr complex.
4. Scrie formula lui Euler.
5. Ce este un modul, argumentul unui număr complex.
6. Ce se întâmplă cu modulele și argumentele atunci când se înmulțește (împărțind).
7. Scrieți formula Moivre pentru gradul n.
8. Scrieți o formulă a rădăcinii ordinii n.
9. Scrieți formulele pentru sine și cosinus generalizate pentru un argument complex.
10. Scrieți formula pentru logaritmul unui număr complex.
Anexa 3. Sarcini de la cursuri.
Articole similare
Trimiteți-le prietenilor: