Soluția unei ecuații liniare omogene cu coeficienți constanți.
Anterior Cuprinsul Următor
O ecuație a formei
se numește o ecuație liniară omogenă cu coeficienți constanți. Soluția sa este compilată pe baza rădăcinilor ecuației caracteristice.
Această ecuație omogenă corespunde ecuației caracteristice:
.
și să aibă rădăcini. atunci:
1) Dacă este o rădăcină reală a multiplicității 1, atunci termenul unei soluții generale a formei
2) În cazul în care - rădăcina reală a k multiplicitate, atunci acesta corespunde termenului de soluția generală a formei în care - polinom (cu coeficienți nedeterminați) cu 1 grad mai puțin decât multiplicitatea rădăcină, care este, de exemplu, dacă rădăcina.
3) Dacă este o pereche de rădăcini complexe conjugate, atunci
4) Dacă - rădăcinile complexe conjugate ale multiplicității k, apoi, respectiv, înaintea cosinusului și sinusului sunt scrise nu doar constante, ci și polinoame de grad k-1.
exemple:
Exemplul 1.
Rezolvați ecuația:
Formăm și rezolvăm ecuația caracteristică
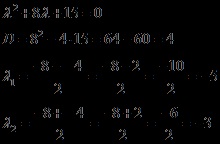
Am obținut două rădăcini reale de multiplicitate 1 (adică, există 1 dintre ele), atunci soluția generală a ecuației omogene va avea forma:
răspundă:
Exemplul 2.
Rezolvați ecuația:
Formăm și rezolvăm ecuația caracteristică
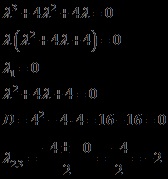
Am obținut trei rădăcini reale.
(multiplicitate - 1) și (din moment ce cele două piese sunt identice, multiplicitatea este 2). atunci soluția generală a ecuației omogene va avea forma:
Notă, deoarece rădăcina -2 are multiplicitatea 2, atunci factorul în suma corespunzătoare nu este pur și simplu C, ci forma generală a polinomului primului grad, adică, grad, la o mai mică multiplicitate a rădăcinii.
răspundă:
Exemplul 3.
Rezolvați ecuația:
Formăm și rezolvăm ecuația caracteristică
Am obținut o pereche de rădăcini complexe conjugate de multiplicitate 1
. atunci soluția generală a ecuației omogene va avea forma:
răspundă:
Exemplul 4.
Rezolvați ecuația:
Formăm și rezolvăm ecuația caracteristică
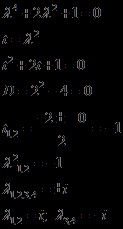
Am obținut două perechi identice de rădăcini complexe conjugate, adică multiplicitate 2
. atunci soluția generală a ecuației omogene va avea forma:
răspundă:
Articole similare
Trimiteți-le prietenilor: