




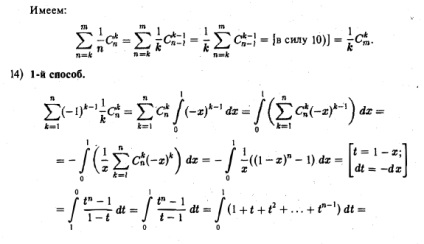

În această secțiune demonstrăm o serie de relații pentru coeficienții binomiali. Toți sunt interesați în ei înșiși și mulți vor fi folosiți de noi în viitor. Cu toate acestea, nu mai puțin interesante sunt metodele de dovedire (sau de primire). Vom oferi, de regulă, dovezi bazate pe natura combinatorică a relațiilor. Schema generală a raționamentului este după cum urmează. Să identitatea dovedită în minte părțile din stânga și din dreapta sarcinii reconstruit pentru numărare un anumit tip de combinații curate (n, m. Acționează ca parametri), decide ca un fel vom obține ca un răspuns. și într-un alt mod - în proporțiile parametrilor menționate mai jos sunt presupuse astfel încât toți coeficienții binomiali face sens (de exemplu, dacă sunt prezente în formula CJ, se presupune că identitatea combinatorii au următoarele identități: 1) pentru fiecare element subset n-element de set livra în corespondență complementul său cu întregul set. Este ușor de observat că, în acest caz, se stabilește o corespondență unu-la-unu între elementele k-element și (n-A) ale elementului n-element. Dacă există o corespondență unu-la-unu între două seturi finite, atunci aceste seturi conțin același număr de elemente. Astfel, numărul de combinații de n pentru a se potrivi cu numărul de combinații de n cu n - k 2) Să n Parlament deputați, inclusiv vorbitor .. Să numărăm numărul de modalități de formare a unei delegații parlamentare de la o persoană. Pe de o parte, acesta este numărul de combinații de CJ. Vom face calculul diferit. Pentru a forma o delegație, inclusiv un vorbitor, este necesar să alegeți dintre deputații obișnuiți n - i k - 1; acest lucru se poate face în moduri. Dacă vorbitorul nu intră în delegație, atunci membrii săi pot fi aleși. (de la n - 1 deputați obișnuiți aleși *, om). Astfel, există totul. modalități de a compune o delegație. 3) 2n este numărul tuturor subseturilor setului n-element. Din moment ce CJ este numărul tuturor subseturilor elementului fc, însumând Cj peste k de la 0 la n, obținem din nou numărul total al tuturor subseturilor. O altă metodă de probă constă în aplicarea unei formule binomiale Newton. Punând x = 1 în ea, obținem cerința necesară. 4) Identitatea este demonstrată prin înlocuirea lui x = -1 în formula de mai sus. De asemenea, oferim o dovadă combinatorie. Să găsim numărul de subseturi dintr-un set n-element care are un număr par de elemente. Coincide cu numărul de modalități de formare a unei delegații parlamentare dintr-un număr par de persoane, dacă sunt doar n deputați în parlament. O delegație arbitrară de acest tip poate fi obținută ca urmare a următoarei proceduri. În primul rând, în ceea ce privește fiecare dintre deputați, fără a lua în considerare vorbitorul, vom decide dacă acest deputat va intra în delegație sau nu. Conform regulii lucrării, aceste decizii pot fi luate de 2P
„moduri. Vorbitorul este inclus în delegație numai în cazul în care există un număr impar de deputați "obișnuiți" în el. Astfel, numărul total de delegații cu un număr par de termeni este de 2n
1, deoarece numărul total de subseturi este 2n, subsetul cu un număr impar de elemente este, de asemenea, 2n_ |, adică același număr ca și cu un număr par de elemente. Prin urmare, deoarece părțile egalității scrise exprimă numărul de subseturi ale setului n-element, respectiv, cu un număr ciudat și par de elemente. Această egalitate este echivalentă cu ceea ce am demonstrat. 5) Această relație este o altă formă de scriere a identității anterioare. Identități combinatoriale 6) Rezolvăm o astfel de problemă. Sunt tone de oameni și n femei. Dintre acestea, trebuie să formați o delegare unei persoane. Câte moduri pot face acest lucru? Răspunsul este evident: cu £ + n. Vom clasifica delegațiile în funcție de numărul de bărbați. Dacă o delegație este formată din bărbați și k - și femei, atunci bărbații pot fi aleși în moduri, iar femeile - în feluri; prin urmare, numărul delegațiilor cu bărbații este egal. Rezumă
a on s de la 0 la k, obținem numărul total de delegații. 7) Pentru dovada, este suficient să se aplice 1) în relația anterioară. 8) Dovada identității poate fi obținută din rezolvarea următoarei probleme: Câte moduri pot alege între n candidați la deputați și printre ultimii vorbitori? Deputații sunt aleși în moduri C, după care vorbitorul este selectat în funcție de metode; Astfel, numărul total de căi este egal cu C "k. Același număr poate fi calculat diferit. Vom alege mai întâi (prin vot popular) un vorbitor (n candidați), iar apoi de la ceilalți candidați n-1 - un alt deputat. Această procedură poate fi efectuată în moduri n • J. Acest lucru este dovedit. Aceasta implică o relație utilă de recurență. 9) Această identitate - generalizarea celei anterioare (dacă punem m = 1 în 9), obținem 8) și se poate dovedi prin rezolvarea unei probleme care este generalizarea considerată anterior: Câte moduri puteți alege între n candidați pentru deputați și printre ultimii membri ai prezidiului? 10) Prima metodă. Să demonstrăm identitatea prin inducția matematică pe k. Baza inducției. Pentru k = 0, avem egalitatea corectă: Pasul de inducție. Să presupunem că afirmația care trebuie dovedită este adevărată. Adăugarea la ambele părți a egalității. obținem astfel relația 10). A doua metodă. Total (subseturi -Element ale acelorași. (Partea dreaptă a acestei identități). Clasificăm aceste subseturi pe cel mai mare element lor, care are în mod evident valori. Vom găsi numărul de subseturi cu cel mai mare element de m + p 4-1. Deoarece cel mai mare element deja selectat m elemente selectate dintr-o multitudine de numere medii de subseturi rămase egale de a rezuma din nou obține numărul total de subseturi -Element (partea stângă a identității necesară) 11) identitatea este dovedită bazată pe cea anterioară: .. 12) Decide Problema m: Câte moduri poți alege între candidații m și printre deputații unor recompense (poate tot, și poate nimeni). Pe de o parte, membrii selectați moduri, și căruia i sa atribuit alocate moduri 2m (ca subseturi având o multitudine de elemente m), și, prin urmare, răspunsul la problema. Pe de altă parte, în cazul în care numărul deputaților acordați este egal cu, atunci ei pot fi aleși în moduri, după care ceilalți deputați sunt aleși în moduri. Sumând peste k de la 0 la m, obținem din nou identități combinatoriale, obținem răspunsul la problema în cauză. Identitatea este dovedită. 13) Folosind relația 8), transformăm termenul general al sumei: a doua metodă. Folosind 13) identitatea, notele și în suma dublă rezultată, schimbăm ordinea sumării
Articole similare
Trimiteți-le prietenilor: