Punctele de inflexiune ale graficului funcției
Definiția. Punctul graficului unei funcții se numește punctul de inflexiune al acestui grafic dacă există o vecinătate a punctului abscisei, în care graficul funcției la dreapta și la stânga punctului are direcții diferite de convexitate.
Dacă funcția este diferențiată într-un punct și în vecinătatea ei, atunci geometric înseamnă că graficul funcției trece într-o vecinătate a unui punct dintr-o parte a tangentei în alta (Figura 3).
Dacă funcția este continuă într-un punct. este diferențiat într-un cartier dintr-un punct. cu excepția punctului în sine. și. atunci graficul funcției într-o vecinătate a punctului este pe laturile opuse ale tangentei verticale (Figura 4).
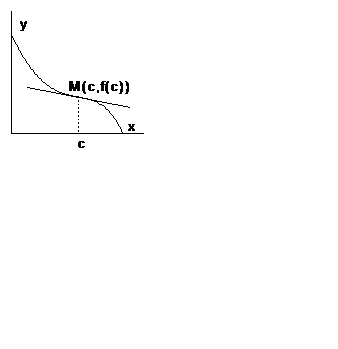
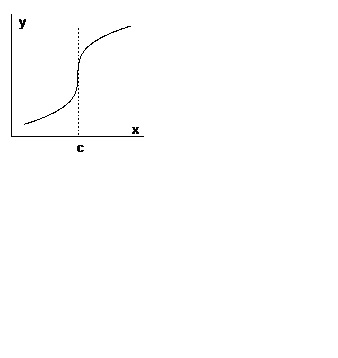
Teorema 3 (condiția necesară pentru existența unui punct de inflexiune). Fie funcția să aibă un derivat continuu secundar în acest punct. Apoi, dacă punctul este punctul de inflexiune al graficului funcției, atunci.
Observăm că condiția este o condiție necesară, dar insuficientă pentru curba graficului funcției la un punct. Luați în considerare, de exemplu, o funcție. Al doilea derivat al acestei funcții. dispare în acest punct. Cu toate acestea, pe întreaga axă numerică. în consecință, peste tot pe această axă, graficul funcției are o convexitate îndreptată în jos și punctul nu este un punct de inflexiune.
Teorema 4 (condiție suficientă pentru prezența unui punct de inflexiune). Dacă funcția este diferențiată într-un punct. este de două ori diferențiată în anumite circumstanțe ale punctului. cu posibila excepție a punctului însuși, iar cel de-al doilea semn al modificărilor derivă semn când argumentul trece prin punct. atunci punctul este punctul de inflexiune al graficului funcției.
Rețineți că dacă funcția este continuă într-un punct. este de două ori diferențiată în anumite circumstanțe ale punctului. cu excepția punctului în sine. și are o tangentă la punctul (cel puțin paralel cu axa), atunci afirmația teoremei 4 este de asemenea adevărată.
Exemplul 1. Găsiți punctele de inflexiune ale graficului funcției.
Să găsim derivatele unei funcții date:
,
.
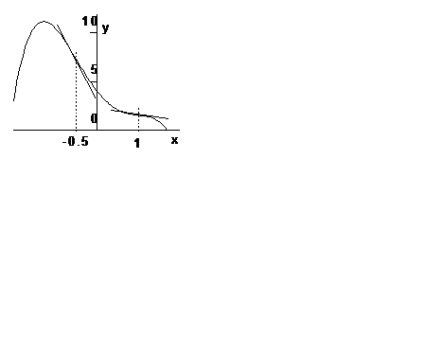
Exemplul 2. Gasiti punctele de inflexiune ale graficului unei functii.
Această funcție este continuă pe întreaga axă numerică și are
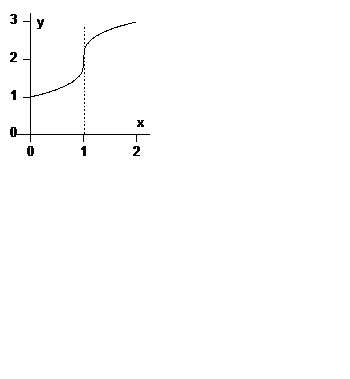
Direcția convexității graficului funcției
Fie funcția să fie diferențiată în orice punct al intervalului. adică are un derivat finit în orice punct al acestui interval. Apoi, există o tangență la graficul funcției. trecând prin orice punct al acestui grafic. Această tangentă nu este paralelă cu axa.
Definiția. Se spune că graficul unei funcții are o convexitate îndreptată în jos (în sus) asupra intervalului dacă graficul acestei funcții este cel puțin (nu mai mare) decât oricare dintre tangentele sale.
În Fig. 1 prezintă graficul unei funcții convexe în jos, iar în Fig. 2 - convex în sus.
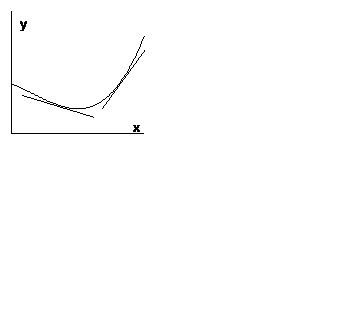
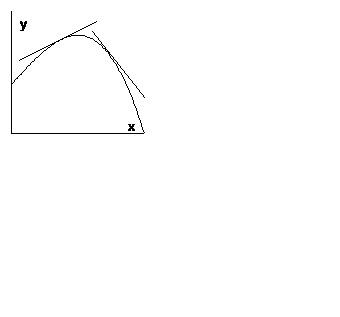
Teoremă 1. Dacă o funcție are un derivat finit secundar pe interval și dacă acest derivat este non-negativ peste tot în acest interval, atunci graficul funcției are o convexitate îndreptată în jos (în sus) asupra intervalului.
Teoremă 2. Fie ca al doilea derivat al unei funcții să fie continuu și pozitiv (negativ) la un punct. atunci există o vecinătate a punctului. în care graficul funcției are o convexitate orientată în jos (în sus).
Articole similare
Trimiteți-le prietenilor: