Intrările cu eticheta "semnificația geometrică a derivatului"
Rezultă ecuația tangentei la graficul funcției y = f (x) într-un punct cu abscisa x0. Pentru claritate, folosim graficul de la
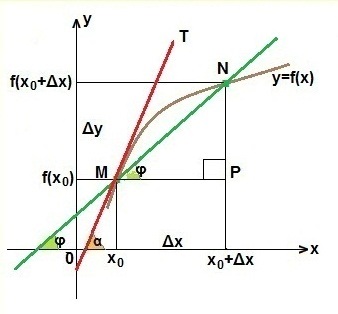
Deoarece am luat punctul M în mod arbitrar, trebuie să obținem o ecuație tangentă care va menține pentru orice funcție y = f (x). având o tangenta la un anumit punct cu abscisa x0.
Deci, orice linie dreaptă poate fi scrisă sub forma y = kx + b. unde k este panta liniei drepte. Acum stim ca ca coeficientul unghiular putem lua f '(x0) - valoarea derivatului functiei y = f (x) intr-un punct cu abscisa x0. Acest punct este un punct comun pentru funcția și pentru MT tangent.
Astfel, MT tangent are forma: y = f '(x0) · x + b. Rămâne să se determine valoarea b. Vom face acest lucru pur și simplu: înlocuiți coordonatele punctului M în ultima egalitate, adică în loc de x se scrie x0. și în loc de y înlocuim f (x0). Obținem egalitatea:
Efectuați următoarele sarcini.
1. Scrieți ecuația tangentei în graficul funcției y = x 2 la punctul x0 = 3. Desenați un desen.
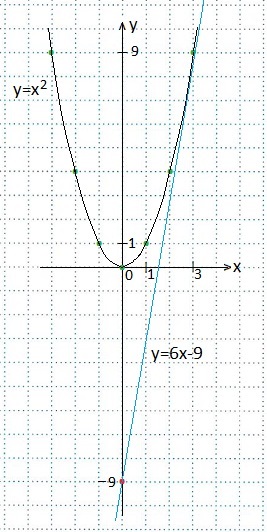
Gasim valoarea acestei functii intr-un punct cu o abscisa data:
Gasim derivatul f '(x) = (x 2)' = 2x si gasim valoarea acestui derivat pentru x = 3.
Înlocuiți valorile găsite
y = 6 x-9 este ecuația dorită a tangentei.
2. Scrieți ecuația tangentei în graficul funcției
Se scrie ecuația generală a tangentei: y = f (x0) + f '(x0) (x-x0). Gasim valoarea acestei functii la punctul x = 1. obținem:
f (x0) = f (1) = 1. Să găsim derivatul unei funcții date prin formula gradului derivat:
Gasim valoarea acestui derivat pentru x = 1.
f '(x0) = f (1) = - 2 (1) -3 = -2. Substituim valorile găsite în ecuația generală a tangentei:
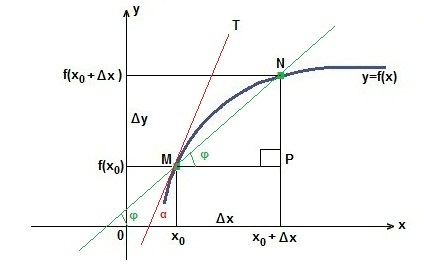
Δy = f (x0 + Δx) - f (x0). Prin punctele M și N tragem secvența MN. care formează un unghi φ cu o direcție pozitivă a axei Ox. Definiți tangenta unghiului φ de la triunghiul dreptunghiular MPN.
Fie Δx tendința de zero. Apoi, secvența MN va avea tendința de a lua poziția tangentei MT. iar unghiul φ devine unghiul α. Prin urmare, tangenta unghiului α este valoarea limita a tangentei unghiului φ:
Definiția derivatului. Limita raportului dintre incrementarea funcției și incrementarea argumentului, atunci când acesta din urmă tinde la zero, se numește derivatul funcției la un anumit punct:
Sensul geometric al derivatului este în acel instrument derivat numeric la un punct dat este egal cu tangenta unghiului format de tangenta trasată prin acest punct la această curbă, iar direcția pozitivă Ox:
1. Gasiti cresterea argumentului si cresterea functiei y = x 2. daca valoarea initiala a argumentului este 4. iar noua valoare este 4.01.
Noua valoare a argumentului x = x0 + Ax. Date substitut: 4.01 + bH = 4, prin urmare, argumentul incrementul bH = 4,01-4 = 0,01. Funcția increment, prin definiție, egală cu diferența dintre valorile noi și anterioare ale funcției, adică, Dy = f (x0 + bH) - f (x0). Din moment ce avem o funcție y = x 2. AU = (x0 + Ax) 2 - (x0) 2 = (x0) 2 + 2x0 · Ax + (Ax) 2 - (x0) 2 = 2x0 · Ax + (Ax) 2 =
A fost posibil să se găsească funcția increment diferit: Dy = y (x0 + Ax) -y (x0) = y (4,01) = y (4) = 4,01 2 -4 2 = 16,0801-16 = 0 , 0801.
Valoarea derivatului în punctul de tangență x0 este tangenta unghiului tangent (semnificația geometrică a derivatului). Avem: f '(x0) = tgα = 1 → α = 45 °, deoarece tg45 ° = 1.
Răspuns: Tangenta la graficul acestei funcții formează un unghi de 45 ° cu direcția pozitivă a axei Ox.
3. Derivează formula pentru derivatul funcției y = x n.
Diferențierea este acțiunea de a găsi derivatul unei funcții.
Când găsim derivați, folosim formule derivate pe baza definiției derivatului, așa cum am derivat și formula pentru gradul derivat: (xn) '= nx n-1.
Tabelul derivatelor va fi mai ușor de învățat prin pronunțarea formulărilor verbale:
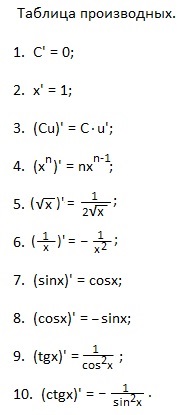
1. Derivatul unei cantități constante este zero.
2. Primul X este egal cu unul.
3. Factorul constant poate fi luat în afara semnului derivatului.
4. Derivatul unei puteri este egal cu produsul exponentului acestui grad cu un grad cu aceeași bază, dar exponentul este unul mai mic.
5. Derivatul rădăcină este egal cu unul împărțit de două rădăcini.
6. Derivatul unității împărțit la x este egal cu minus unul împărțit la x în pătrat.
7. Derivatul sinusului este egal cu cosinusul.
8. Derivatul cosinusului este minus sinusul.
9. Derivatul tangent este egal cu unul împărțit la pătratul cosinusului.
10. Derivatul cotangentului este egal cu minus unul împărțit la pătratul sinusului.
Aflați regulile de diferențiere.
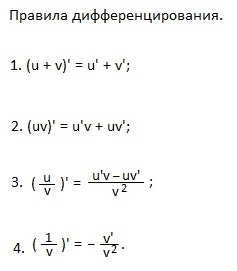
2. Derivatul produsului este egal cu produsul derivatului primului factor cu cel de-al doilea plus produsul primului factor cu derivatul celui de-al doilea factor.
3. Derivat „y“ împărțită „CE“ este fracțiunea în care numărătorul „în bara multiplicat cu“ CE „minus“ uneori bara ve „iar numitorul -“ ve în piață ".
Pagina 1 din 1 1
Trimiteți-le prietenilor: