Ne amintim definițiile de bază ale teoriei grafurilor. Fie V un set finit non-gol. Semnificăm prin V (2) mulțimea tuturor subseturilor cu două elemente ale lui V. Un grafic G este o pereche de seturi (V.E), unde E este un subset arbitrar de V (2). Elementele seturilor V și E sunt denumite, respectiv, vârfurile și marginile graficului G. Graficul G (V.E) este numit complet. dacă o pereche de vârfuri este conectată în cel puțin o direcție.
O rută (sau o cale) într-un grafic G este o secvență alternantă de vârfuri și muchii v 0. e 1. v 1. ..., v t -1. e t. v t + 1. în care e i = v i -1 v i (1 ≤ i ≤ t). Un astfel de traseu este numit pe scurt (v 0. v t) - traseul și se spune că se conectează v 0 c v t; la rândul lor, vârfurile v 0. v t sunt vârfurile de sfârșit ale rutei specificate. Lungimea căii este numărul de coaste pe care le conține. Rețineți că într-un grafic obișnuit traseul este complet determinat de secvența v 0. v 1. ..., v t a vârfurilor sale. Dacă v 0 = v t. apoi (v 0. v t) - traseul se numește închis.
Un lanț este un traseu fără repetarea coastelor. Un lanț este numit lanț simplu dacă nu are noduri repetate, cu excepția, probabil, vârfurile terminale coincide. Un lanț simplu închis este numit un ciclu (sau contur).
Lanțul Hamiltonian al unui grafic este lanțul său simplu, care trece prin fiecare vârf al grafului exact o dată. Un ciclu al unui grafic care trece prin fiecare vertex este numit un ciclu Hamiltonian. Un grafic este numit Hamiltonian. dacă are un ciclu Hamiltonian.
Aceste nume de lanțuri și cicluri asociate cu numele lui William Hamilton (Hamilton W.), care în 1859 a propus următorul joc de puzzle, este necesar trece pe rând de la un nod la altul vârf al dodecaedrul pe marginea sa, pentru a ocoli toate cele 20 de vârfurile o dată și reveniți la vârful inițial.
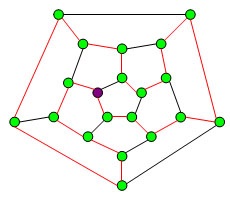
Rețineți că au fost inventate multe alte probleme distractive și utile legate de căutarea ciclurilor Hamiltonian. Formăm două dintre ele.
- (Problema banchetului) O companie de mai mulți oameni trebuie să se așeze la o masă rotundă în așa fel încât să fie cunoscuți de fiecare parte a fiecăruia. Evident, pentru a rezolva această problemă, trebuie să găsiți ciclul Hamiltonian în graficul de întâlnire al companiei.
- (Problema calului eșalonat.) Este posibil, pornind de la un câmp arbitrar al tabloului de șah, să parcurgeți toate cele 64 de câmpuri unul câte unul și apoi să reveniți la câmpul original? (soluția va fi luată în considerare mai jos).
Următoarea teoremă, dovedită de Posh (Posa L.), dă o condiție suficientă pentru ca graficul nedirecționat să fie Hamiltonian. Acesta generalizează rezultatele obținute anterior de Ore (Ore O.) și Dirac (Dirac G.A.), care sunt date aici sub formă de consecințe.
Fie G p ≥ 3 vârfuri. Dacă pentru fiecare n. 1 ≤ n ≤ (p -1) / 2, numărul de noduri cu puteri care nu depășesc n. este mai mică decât n. și pentru un paragraf p numărul de vârfuri de grad (p -1) / 2 nu depășește (p -1) / 2, atunci G este un grafic Hamiltonian.
Dovada. Să presupunem că teorema este falsă, iar G să fie un grafic maxim non-hamiltonian, cu vârfuri p satisfăcătoare condițiilor teoremei. Este ușor de observat că adăugarea oricărei margini într-un grafic care posedă proprietățile indicate în teorema conduce la un grafic care are și aceste proprietăți. Astfel, deoarece adăugarea unei margini arbitrare la G conduce la un grafic Hamiltonian, oricare două noduri neadiacente sunt conectate printr-un lanț simplu de acoperire (conținând toate vârfurile graficului).
Mai întâi arătăm că fiecare vertex al cărui grad este cel puțin (p -1) / 2 este adiacent fiecărui vârf cu o putere mai mare decât (p -1) / 2. Să presupunem (fără pierderea generalității) că deg v 1 ≥ (p -1) / 2 și deg v p ≥ p / 2, dar nodurile v 1 și v p nu sunt adiacente. Apoi, există un lanț simplu spanning v 1 v 2 ... v p. conectarea v 1 și v p.
Noi denotăm nodurile adiacente v 1. prin v i 1, ..., v i n. unde n = deg v 1 și 2 = i 1 v 1 v 2 ... v i j -1 v p v p -1 ... v i j v 1.
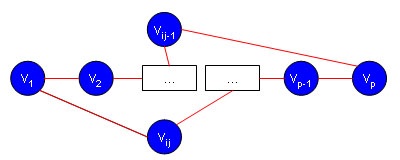
Mai mult, deoarece n ≥ (p -1) / 2, atunci p / 2 ≤ deg v p ≤ p -1-n
Rezultă că dacă deg v ≥ p / 2 pentru toate nodurile v. atunci G este un grafic Hamiltonian. (Aceasta este prezentată mai jos sub forma Corolarului 2). În virtutea celor de mai sus, fiecare pereche de vârfuri ale graficului G este adiacentă, adică G este graficul complet. Am ajuns la o contradicție, deoarece graficul complet este Hamiltonian pentru toate p ≤ 3.
Astfel, în G există un vertex v cu deg v
Condiția suficientă de mai sus nu este necesară. Graficul cubic descris în figură este un hamiltonian, deși este clar că nu satisface condițiile teoremei. Cu toate acestea, condițiile teoremei sunt neimportante, deoarece atunci când sunt slăbite, noua condiție nu va mai fi suficientă pentru ca graficul să fie Hamiltonian.
Restricționând condițiile teoremei Poth, obținem condiții mai simple, dar mai puțin suficiente, găsite de Ore și Dirac, respectiv:
Corolarul 1
Dacă p ≥ 3 și deg u + deg v ≥ p pentru orice pereche u și v de vârfuri neadiabile ale lui G. atunci G este un grafic Hamiltonian.
Corolarul 2
Dacă p> 3 și deg v ≥ p / 2 pentru orice vertex v al graficului G. atunci G este un grafic Hamiltonian.
În graficul complet G (V.E) există întotdeauna o cale Hamiltoniană.
Dovada. Fie m = a 1 a 2 ... a p o cale de lungime p -1, iar toate nodurile în m sunt distincte. x este vârful ∉ m. Arătăm că putem compune o cale a formei
Să presupunem că nu există un astfel de număr întreg k. încheiat între 1 și p. că
Prin urmare, avem 1 ≤ k ≤ p.
(a k x) ∈ E → (x, a k + 1) ∉ E → (a k + 1, x) ∈ E.
Dacă nu există nici o cale m 0 = x a 1 ... a p. atunci (a 1. x) ∈ E → (a 2. x) ∈ E. (a p. x) ∈ E. și calea m p = a 1 ... a p x există, contrar presupunerii. Astfel, puteți pași pas cu pas pentru a construi o cale care să conțină toate vârfurile graficului. ♦
Notă. Din acest rezultat rezultă că este întotdeauna posibil să se comande o mulțime de participanți la turneu în așa fel încât fiecare dintre aceștia să fie câștigătorul direct al următorului (dacă, bineînțeles, niciuna dintre întâlniri nu se termină la egalitate).
Problema calului eșuat
Vom seta sarcina de a ocoli placa de șah astfel încât să vizitați fiecare celulă exact o dată. Această problemă a fost de interes pentru mulți matematicieni, în special Euler L., de Moivres, Vandermonde și alții.
O regulă care, aparent, este justificată în practică, dar în teorie nu a fost încă confirmată este următoarea: de fiecare dată când mergem cal înapoi în cazul în care amenință cel mai mic număr nu a fost încă adoptată de către celule.
O altă modalitate este de a găsi ruta de-a lungul semiprofesiei, duplicarea simetrică a acesteia și conectarea ambelor rute.
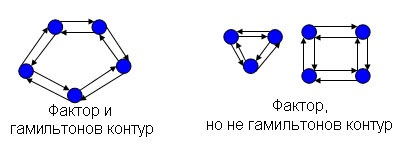
Grafic Factor (V. E) se numește graficul parțial (V. E 0), în care fiecare nod are outdegree și setarea egală cu 1. Cale Fiecare hamiltonian este un factor, dar reciproca nu este adevărat, deoarece factorul poate fi compus din mai multe circuite nu au noduri comune .
EA = ∪ u ∈ A Eu.
și anume EA este imaginea setului de vertex A.
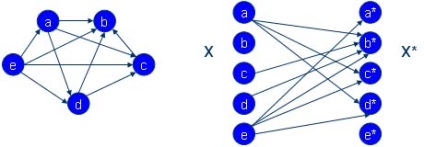
Definiți un grafic simplu (V. V * E.) Corespunzător acestui grafic arbitrar (V. E), după cum urmează: V * este un duplicat al setului V. av * k ∈ Ev i în (V. V * E.) Dacă și numai atunci, atunci când vk ∈ Ev i în (V. E).
Teorema 3 (Konig D. Hall P.)
O pereche care arata V in U. exista daca si numai daca | EW | ≥ | W | pentru orice set W ⊂ V.
Fie (V.U.E) un grafic simplu, a
atunci există întotdeauna o potrivire care utilizează toate acele noduri v. pentru care | Ev | = m. și toate acele noduri u. pentru care | E-1 u | = m.
O condiție necesară și suficientă pentru existența unui factor într-un grafic (V.E) este aceea că | EW | ≥ | W | pentru toate W ⊂ V.
Dovada. Într-adevăr, prin teorema 3, această condiție exprimă faptul că într-un simplu grafic (V.V * .E), există o potrivire care hărțuie V la V *. ♦
Dacă graficul (V.E) este astfel încât | Ev | = | E -1 v | = m pentru orice vârf v. atunci arcele acestui graf pot fi distribuite pe seturi disjuncte m W 1. W 2. ..., W m. fiecare dintre ele constituind un factor.
Dovada. Un grafic simplu (V.V * .E) posedă proprietatea | Ev | = m. | | E-1 v * | = m. Corolarul Teorema 3 poate fi mapat la V V * și prin aceasta determină W 1. Graficul parțială rămasă după îndepărtarea arcurilor 1. W poate fi afișat pe V V * și, astfel, determină W 2, etc. ♦
Găsirea unui factor este o problemă simplă, deoarece este problema celui mai mare flux. Metoda de a găsi conturul Hamiltonian este de a găsi toți factorii din grafic și de a păstra numai aceia dintre aceștia care constau dintr-un singur contur.
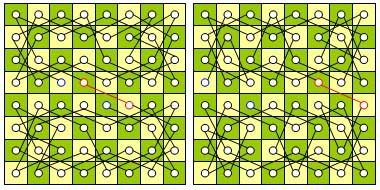
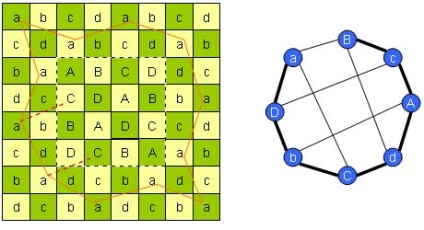
De asemenea, puteți "lipi" diferitele contururi ale factorului. Luați în considerare din nou problema calului eșalonat. Datorită simetriei plăcii de șah, se obține factorul prezentat în figură. Celule marcate cu aceleași litere formează un contur. Două contururi pot fi combinate dacă și numai dacă două vârfuri succesive ale unuia sunt adiacente la două vârfuri consecutive ale celeilalte. Diferite conexiuni sunt afișate utilizând graficul auxiliar. Graficul auxiliar are calea Hamiltoniană evidentă aDbCdAcB.
Algoritmul pentru găsirea ciclului Hamiltonian
Luați în considerare funcția de căutare recursivăHamiltonianCycle. care se întoarce adevărat. dacă graficul este Hamiltonian și altfel fals.
- numberOfVertices - numărul de vârfuri din grafic
- v - ultimul vârf găsit
- w - vârful inițial (căutarea începe de la acesta)
- d este lungimea rămasă a ciclului Hamiltonian
Acest algoritm seamănă cu un algoritm de căutare în profunzime (DFS). Principalele diferențe sunt marcate cu roșu:
- funcția ia vârful inițial w și lungimea ciclului Hamiltonian ca al doilea și al treilea parametru, respectiv;
- în linia 1, funcția verifică dacă toate nodurile au fost vizitate (d == 1) și dacă există, există o margine care leagă vertexul inițial cu vârful final. Dacă ambele condiții sunt îndeplinite, atunci se găsește ciclul Hamiltonian;
- în linia 7, funcția restabilește valoarea marcatorului vizitat. înainte de a reveni la o valoare care indică o eroare.
O căutare recursivă pentru un ciclu Hamiltonian poate necesita un timp exponențial.
Dovada. Luați în considerare un grafic a cărui vertex este izolat și marginile care leagă restul | V | -1 vârfurile formează un grafic complet. Funcția searchHamiltonianCycle nu va găsi niciodată un ciclu Hamiltonian, dar el explorează tot (| V | -2)! căi începând de la vârful inițial selectat, fiecare dintre ele folosind | V | -1 apeluri recursive. Prin urmare, numărul total de apeluri recursive este (V -1). ♦
Referințe
visualizers
Trimiteți-le prietenilor: