Independența liniară
O combinație liniară de șiruri de caractere el. e2. ek este suma produselor acestor rânduri prin numere reale arbitrare:
e = l el + 2 e2 +. + k ek. unde l. 2. k sunt numere arbitrare (coeficienții unei combinații liniare).
Rândurile matricei el. e2. em sunt numiți liniar dependenți. dacă există numere l. 2. m. nu egal cu zero în același timp, că combinația liniară de rânduri a matricei este egală cu linia zero:
l el + 2 e2 +. + m em = 0, unde 0 = (0 0 0).
Dependența liniară a rândurilor matricei înseamnă că cel puțin un rând al matricei este o combinație liniară a celorlalte. Într-adevăr, să presupunem pentru definitivitate ultimul coeficient m 0. Apoi, împărțind ambele părți ale egalității cu m. obținem expresia pentru ultima linie. ca o combinație liniară a liniilor rămase:
em = (l / m) el + (2 / m) e2 +. + (m-1 / m) em-1.
Dacă combinația liniară de rânduri este zero dacă și numai dacă toți coeficienții sunt zero, adică l el + 2 e2 +. + m em = 0 k = 0 k, atunci liniile sunt numite liniar independente.
O teoremă privind rangul unei matrice. Rangul matricei este egal cu numărul maxim al rândurilor sau coloanelor sale liniar independente. prin care puteți exprima liniar toate celelalte rânduri sau coloane.
Să dovedim această teoremă. Să presupunem că o matrice A de m x n are rang r (r (A) min). În consecință, există un minor non-zero de ordin r. Orice astfel de minor va fi numit de bază. Pentru claritate, permiteți-i să fie minor
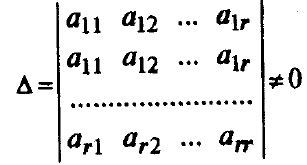
De asemenea, numim rândurile acestui element minor.
Să arătăm că atunci rândurile matricei el. e2. er sunt independente liniar. Să presupunem contrariul, adică una dintre aceste linii, de exemplu r, este o combinație liniară a celorlalte: er = l el + 2 e2 +. + r-1 er-1 = 0. Apoi, dacă scăpăm din elementele rândului r elementele din primul rând înmulțit cu l. elemente din al doilea rând, înmulțite cu 2. și așa mai departe. în final, elementele rândului (r-1) înmulțit cu r-1. atunci rândul r devine zero. În același timp, determinantul de mai sus nu trebuie să se schimbe în funcție de proprietățile determinantului. și trebuie să fie zero în același timp. Se obține o contradicție, independența liniară a rândurilor este dovedită.
Acum dovedim că orice (r + 1) rânduri ale matricei sunt dependente liniar; orice șir poate fi exprimat în termeni de bază.
Completăm minorul considerat anterior cu un rând mai nou (i-a) și încă o coloană (j-m). Ca rezultat, obținem o ordine minoră (r + 1), care prin definiție de rang este zero:
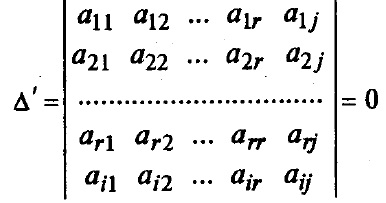
Extindem-o pe elementele coloanei j. Aici, ultimul complement algebric Aij coincide cu minorul de bază 0 Aij 0. Prin urmare, putem împărți ambele părți ale ultimei egalități de Aij. Acest lucru va exprima elementul din acesta :.
Dacă fixăm numărul rândului (i), atunci obținem că pentru orice j elementele rândului i sunt exprimate liniar în termeni de elemente ale rândurilor de bază :, orice rând al matricei este o combinație liniară a celor de bază.
Trimiteți-le prietenilor: