Un oscilator armonic este un sistem care efectuează oscilații descrise de o ecuație a formei (140.6):
Oscilațiile unui oscilator armonic sunt un exemplu important al mișcării periodice și servesc ca un model precis sau aproximativ în multe probleme ale fizicii clasice și cuantice. Exemple sunt arc oscilator armonic, circuit de pendul oscilație fizică și matematică (pentru curenți și tensiuni joase, astfel încât elementele de buclă ar putea fi considerate ca fiind liniare, vezi §146.).
1. Un pendul de primăvară este o masă de greutate. suspendat pe un arc absolut elastic și efectuând oscilații armonice sub acțiunea unei forțe elastice F = - k x, unde k este coeficientul de elasticitate, în cazul unui arc numit rigiditate. Ecuația de mișcare a pendulului
Din expresiile (142.1) și (140.1) rezultă că pendulul de primăvară efectuează oscilații armonice conform unei legi cu o frecvență ciclică
Formula (142.3) este valabil pentru vibrații elastice în limitele în care legea Hooke (cm. (3.21)), m. E. Când masa de primăvară este mică în comparație cu corpul de masă.
Energia potențială a pendulului de primăvară, conform (141.5) și (142.2), este
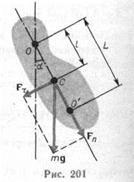
2. Un pendul fizic este un corp solid care, sub acțiunea gravitației, oscilează în jurul unei axe orizontale fixe a suspensiei care nu trece prin centrul masei C a corpului (figura 201).
Dacă pendulul este deviat de poziția de echilibru cu un unghi. apoi în conformitate cu ecuația dinamicii mișcării de rotație a unui corp rigid (18.3), momentul M al forței de refacere poate fi scris în forma
în care - momentul de inerție al pendulului în jurul unei axe care trece prin punctul O, l - distanța dintre punctul de suspensie și centrul masei pendulului; - restabilirea forței (semnul minus se datorează faptului că direcțiile și întotdeauna opuse; corespunde mici oscilații ale pendulului, adică mici ... deviațiile pendulului din poziția de echilibru).
Ecuația (142.4) poate fi scrisă în formular
identic cu (142.1), a cărui soluție (140.1) este cunoscută:
Rezultă din expresia (142.6) că pentru oscilații mici pendulul fizic efectuează oscilații armonice cu o frecvență ciclică (a se vedea (142.5)) și o perioadă
unde L = J / (ml) este lungimea redusă a pendulului fizic.
Punctul O 'al prelungirii liniei drepte OS, separat de axa suspensiei printr-o distanță a lungimii reduse L., este numit centrul oscilațiilor pendulului fizic (Figura 201). Aplicând teorema Steiner (16.1), obținem
adică, OO "este întotdeauna mai mare decât OC. Punctul de suspendare O și centrul de oscilație O 'au proprietatea de interschimbabilitate. dacă axa suspensiei este transferată în centrul oscilațiilor, atunci punctul O al axei de suspensie anterioare devine un nou centru de oscilații și perioada de oscilații a pendulului fizic nu se modifică.
3. Un pendul matematic este un sistem idealizat constând dintr-un punct de masă de masă m. suspendat pe un fir inextensibil fără greutate și oscilând sub influența gravitației. O bună aproximare a unui pendul matematic este o mică minge greu suspendată pe un fir subțire lung.
Momentul inerției unui pendul matematic
unde l este lungimea pendulului.
Deoarece pendulul matematic poate fi descris ca un caz special al unui pendul fizic, presupunând că toată masa sa concentrat într-un singur punct - centrul masei, apoi înlocuind expresia (142,8) în formula (142,7), obținem o expresie pentru perioada de oscilație a pendulului matematic mici
Comparând formulele (142.7) și (142.9), vedem că dacă lungimea redusă L a unui pendul fizic este egală cu lungimea l a unui pendul matematic, atunci perioadele de oscilații sunt aceleași. În consecință, lungimea redusă a unui pendul fizic este lungimea unui astfel de pendul matematic al cărui perioadă de oscilație coincide cu perioada de oscilație a unui pendul fizic dat.
Trimiteți-le prietenilor: