La proiectarea, dezvoltarea și evaluarea calității oricăror sisteme complexe, care includ și sisteme software, este nevoie de implementarea unui sistem de cerințe foarte contradictorii. Dacă aceste cerințe către sistem pot fi exprimate sub forma unui anumit set de indicatori cantitativi parțiali (criterii specifice - criteriile h), atunci problema de proiectare poate fi formalizată sub forma unei probleme vectoriale multicriteriale de programare matematică (VZMP):
unde (1) înseamnă că o creștere a oricăror criterii r îmbunătățește calitatea sistemului; [1] X = (xj) n - parametrii LPR de decizie controlați de factorul de decizie; Dx este domeniul soluțiilor admisibile ale LPR.
Mai mult, vom presupune că η-criteriile sunt lineare, iar domeniul este închis și limitat de inegalități liniare. Apoi, problema multicriterială (vector) LP (VZLP) poate fi scrisă sub forma:
unde restricțiile asupra dreptului sunt reprezentate ca funcții liniare non-negative (variabile) [2].
VZLP (3), (4) nu este o problemă de optimizare, deoarece este posibil să se vorbească despre optimitatea soluției doar în sensul unuia dintre un criteriu h din totalitatea lor (3). În ceea ce privește întregul set (3), putem vorbi doar despre o soluție rațională, într-o măsură mai mare sau mai mică, practic acceptabilă, de compromis, în care, probabil, nici unul dintre criteriile de rată nu ia valoarea maximă. Sunt propuse diferite proceduri pentru căutarea soluțiilor raționale [1-8], dar condiția necesară pentru fiecare astfel de soluție este imposibilitatea de a-l îmbunătăți cu cel puțin un criteriu h, astfel încât nici unul dintre celelalte să nu-și deterioreze valoarea. O astfel de soluție "neimportantă" este de obicei numită Pareto optimă [1-3] sau abreviată P-optimă.
Astfel, soluția la orice sarcini multiobiectiv sau începe să caute întregul set de soluții n-optime (n-set), care ar trebui să fie, și final, compromisul sau finisaje de verificare soluții preformate în n-optimalitate și, dacă este necesar, îmbunătățirea ulterioară a acestuia pentru unele h-criterii, fără o deteriorare a valorilor rămase.
Scopul principal al acestei lucrări este de a formula un algoritm destul de simplu și ușor formalizabil care să permită determinarea:
- întregul set de soluții Pareto-optimale ale VZLP (Dpx);
- dacă soluția X este P-optimă și, dacă este necesar, găsiți cea mai apropiată soluție P.
Baza metodei propuse este condiția formală a optimizării P a soluției X ¢ [1; 2]: soluția X ¢ÎDx este P-optimal dacă nu există altă soluție XÎDx, conform căruia sunt îndeplinite următoarele condiții:
"k": Lk (X) ³ Lk (X ¢), adică Dk = Lk (X) -Lk (X ¢)
cel puțin unul dintre ele este strict (Dk1> 0).
Pentru formularea algoritmului, este convenabil să reprezentăm condiția (5) sub forma problemei Lp (3nP):
sub constrângerile Dk = Dk (X) ≥0, "k = 1; r. (7)
Condițiile (7) în sensul geometric sunt o anumită regiune formată prin intersecția spațiilor semi-dimensionale r n-dimensionale definite de inegalități (7). În cazul compatibilității, sistemul (7) formează un anumit spațiu - un con cu vârful X ¢. Fiecare punct al acestui con este îmbunătățit, în comparație cu X ¢, o soluție (în continuare acest con este numit con de dominație, d-con).
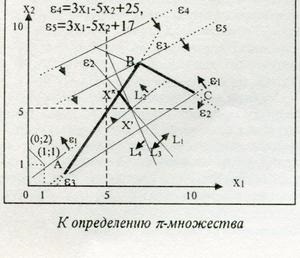
La definirea unui set p
În figură, partea conului situat în regiunea Dx este reprezentată de segmentul X ¢, Xp pentru următorul WVLP:
L2 (X) = - x1 + x2 + 10, ımax e2 = -x1-4x2 + 34, Dx
L3 (X) = -x1-x2 + 16, Xe3 = 2x1-x2-5,
L4 (X) = - 2x1-x2 + 30, (8) "i, j: xj,
Degenerarea conului d se datorează opusului complet al criteriilor h L1 și L3 - gradienții lor vectori diferă numai în semne. Din punct de vedere fizic, un astfel de caz nu poate avea loc. dacă, de exemplu, L1 necesită maximizarea fiabilității sistemului, atunci L3 - minimizarea aceleiași fiabilități. Cu toate acestea, o examinare formală a unui astfel de sistem de criterii y nu își pierde semnificația.
Schimbarea punctului de X ¢ în e-con, o soluție îmbunătățită. Această îmbunătățire (în acest caz, criteriul h-L2), eventual, până la un punct Xp deplasare atunci când întregul con-d, cu excepția vârful său, va fi în afara domeniului Dx. Deoarece alegerea punctului X ¢ nu afectează forma și orientarea d-con (care corespunde cu deplasarea paralelă în Octant n-dimensional), este posibil, prin alegerea X ¢ puncte diferite Dx să rețineți că toate suma P-mnozhstvo puncte de pe margini (margini) AB și BC model.
Astfel, a soluțiilor ZLP (6), (7), pentru orice alegere de top d-con X ¢ în Octant pozitiv [3] următoarele concluzii: dacă Dmax> 0, atunci d-cone există și suma set-P la anumite fețe ale pluralității dx; dacă Dmax = 0, atunci (7) este compatibil numai la X ¢, ceea ce înseamnă că orice punct al X ¢ÎDx este P-optimal (Dpx = Dx).
În cazul Dmax> 0, punctul X ¢ trebuie să fie selectat succesiv pe fiecare dintre fețele lui Dx. Aceasta este echivalentă cu adăugarea la sistem (7) a unei încă inegalități corespunzătoare feței i (eiφ0). Dacă criteriul D (6) crește în cursul soluției, atunci această față nu este P-optimă, iar dacă Dmax = 0, fața intră în setul Dpx. După verificarea tuturor fețelor m ale lui Dx, găsim setul D-D din setul P.
Setul de transfer (6) de pe muchie Dx asociată cu calcule suplimentare, însă vertex X ¢ d-con este recomandabil să se aleagă un punct fix X ¢ = (1) [4] și aceeași față a punctului de transfer simplex Dx. Apoi, scăderea transformărilor elementare, redus la punctul X ¢ = (1) n ZLP (6) și (7) poate fi scrisă ca:
În acest caz, chipurile transformate ale simplexului sunt scrise:
Se ilustrează procesul de soluție utilizând exemplul (8), (9). În conformitate cu (10) - (11), scriem SLA în sistem (12) în forma algebrică și tabelară T1:
T1 x1 x2 1 T2 x1 D1 1 T3 e2 D1 1
D = -3x1 + 3xmax, D -3 0 3 D -3 0 3 D -1 -4 0
D1 = x1 + x2-2, D1 1 1 -2 x2 -1 1 2 x 2 1
D2 = -x1 + x2, D2 -1 1 0 D2 -2 1 2 D2 0
D3 = -x1-x2 + 2, D3 -1 -1 2 D3 0 -1 0 D3 0 (13)
D4 = -2x1-x2 + 3, D4 -2 -1 3 D4 -1 -1 1 D4 0
e1 = -5x1 + 7x2-2, e1 -5 7 -2 e1 -12 7 12 e1 0
e2 = -x1-4x2 + 5, e2 -1 -4 5 e2 3 -4 -3 x1 1
e3 = 2x1-x2-1. e3 2 -1 -1 e3 3 -1 -3 e3 0
Metoda de îmbunătățire succesivă a planurilor [6, 7] rezolvă APL, traversată în T1 printr-o linie dublă. Limitările ei, înregistrate sub linia dublă, sunt pur și simplu recalculate în conformitate cu formulele excepțiilor obișnuite ale Iordaniei (OZHI). După etapa OZHI (înlocuirea lui D1 "x2, T1) se obține soluția optimă. Deoarece Dmax 0 (Dmax> 0), d-conul există și, în consecință, setul p va forma unele fețe ale lui Dx. Aceste fețe sunt determinate prin eliminarea acelor fețe care nu pot intra în Dx. Pentru ei, pentru D> 0, avem εφ0 (fata e1). Numerele i ale fețelor rămase formează setul I- =. Verificarea secvențială a fețelor iÎI - dezvăluie fețele epi. Astfel, de exemplu, adăugarea în sistem (11) a feței e2<0, после шага ОЖИ (e2«х1,Т2) получим решение X0=(1;1) и Dmax=0, из чего следует p-оптимальность грани e2 области Dх. То же для e3 (см.рис.).
DPH pentru a proteja împotriva soluțiilor false ale sistemului (4) fețe ar trebui să fie excluse nu formează limitele domeniului Dx. Pentru această serie „ei³0 înlocuite EI la limită = 0. Dacă sistemul (4) devine incompatibil, atunci ei³0 inegalitatea este eliminată. Exclus și inegalitate liniar dependente (vezi. Fig. E4, E5) [5]. Presupunând că se formează acest screening- , putem scrie procedura pentru rezolvarea problemei.
Algoritmul pentru determinarea setului p
20. Rezolvați LPA (10), (11), recalculând simultan (12)
30. Dacă Dmax = 0, scrie Dpx = Dx, mergeți la 110
40. Eliminați restricțiile eiφ0 de la (12), notați (specificați) setul I - =
50. Dacă I = 0, mergeți la (100)
60. Includeți fața ei, iÎI - în sistem (11) și rezolva LPA (10), (II) + ei
70. Dacă Dmax10, i este exclus din I-, mergeți la 40
80. Include fata ei în Dpx (ei = epi), exclud din I-
90. Dacă I-¹0, mergeți la 60
Dacă se găsește Dpx, atunci întrebarea dacă un punct arbitrar X ¢ îi aparține reduce la înlocuirea componentelor x ¢ j în (9) și la calculul reziduurilor ei. Dacă pentru orice non-negativitate non-negativă, cel puțin una dintre ele care corespunde unui set P este egală cu zero, atunci X ¢ÎDPH.
Cu toate acestea, pentru a verifica optimitatea π-a lui X, nu este necesară construirea întregului set P. Este suficient să rezolvăm APL (6), (7), (4). Dacă Dmax = 0 - punctul X ¢ este P-optimal. Pentru Dmax¹0, se va găsi o soluție îmbunătățită (vezi Figura X ¢ și Xp).
Sa demonstrat în [8] că setul PZ VZLP poate fi găsit ca set de soluții ale ZLP sub constrângeri (4) și cu funcția obiectivă obținută ca o combinație liniară a criteriilor h: [6]
cu toate valorile posibile ale coeficienților de greutate ai criteriilor u - ak.
Dezavantajul acestei abordări este că pot fi detectate numai soluțiile P situate pe limitele domeniului Dx. În cazul [2], pentru cazul Dpx = Dx, se propune alegerea unui vector de coeficienți ao = (ak), pe care toți coeficienții cj din "convoluția" (14) dispare. O astfel de abordare poate introduce soluții false Π. De exemplu, luând a0 = (0.5; 0; 0.5; 0) pentru sistemul (8), ar trebui să concluzionăm că Dpx = Dx, dar este evident din figură că nu este cazul.
Indicăm procedura de calcul, care pune în aplicare principiul „convoluție“ și care se adresează această deficiență. Metoda constă în aceea că pentru detectarea P-luare situat pe i-lea fata (4), este necesar, prin alegerea vectorului AI îndeplinească două condiții: cj coeficienți (14) și aij i-lea feței trebuie să fie proporțională de fiecare dată j; Acești factori ar trebui să aibă semne diferite, care va oferi o valoare extremă „convoluție“ în i-lea (i = 1; m) față. Presupunând proporționalitate coeficient hi pozitiv, aceste condiții având în vedere (14) poate fi scrisă ca:
Pentru fata i-lea sistemul de ecuații (16) este în continuare pregătită, soluția care ne permite să se stabilească dacă există la hi> 0 vector ai = (AIK), care pune în aplicare condițiile necesare pentru această față.
Incorecta semnalată anterior este conectată formal cu cazul când hi = 0 în (16). Pentru ao elimina, este suficient să asociați cazul Dpx = Dx cu situația în care toate m facetele dx simplectic sunt incluse în setul Π. Aceasta va ieși la lumină după verificarea tuturor fețelor m. Astfel, definiția unui set P în cadrul acestei abordări se reduce la o soluție de m-ori a sistemului (16), sau mai precis, la soluția unui LFA: [7]
unde Oj sunt variabile care trebuie să fie zero (variabile zero); hi este coeficientul de proporționalitate.
Trebuie remarcat faptul că atât în primul și în al doilea caz pentru a aduce o soluție la sfârșitul anului ZLP, de obicei, nu are nici un sens. Este suficient să se asigure că numai D> 0 (primul algoritm) sau hi> 0 (al doilea algoritm), care asigură împotriva concluzii eronate cu privire la fața nu-verificate.
Algoritmul 2 pentru determinarea setului p
30. Rezolvați SLA (17), (18) (maxh)
40. Dacă hmax £ 0, eliminați fața ei, mergeți la 60
50. Scrie ei = epiÎDPH
80. Dacă | Dpx | ¹m, mergeți la 100
90. Scrie Dpx = Dx
Soluțiile obținute în conformitate cu algoritmul de mai sus sunt după cum urmează:
h1max = 0, (AC); h2 = 0,1, (BC); h3 = 1/7, (AB). (19)
După cum se poate observa din (19), fața AC nu intră în setul Π (h1max> 0).
Cu aceeași simplitate computațională a ambilor algoritmi, numai prima abordare are următoarele trei caracteristici:
- este posibil să se verifice optimitatea P a oricărei soluții X ¢ÎDx, și pentru VZLP și pentru a găsi cel mai apropiat P-optimal fără a recurge la căutarea întregului set P;
- cazul Dpx = Dx este detectat chiar la începutul calculelor, după care dispare nevoia de calcule ulterioare;
- fără complicații suplimentare, este posibil să se verifice optimitatea P a unui anumit punct X ¢ arbitrarÎDx în problema generală a MP (1), (2).
În acest din urmă caz, este suficient ca o serie de date inițiale || Ckj || utilizați matricea valorilor derivatelor la punctul X ¢ÎDx (aproximare):
Răspunsul este obținut sub formă de „da“, „nu“, nu conține nici o indicație (în cazul „nu“) cu privire la direcția de cercetări ulterioare soluțiilor P optime. În cazul în care „da“ poți vorbi doar despre soluțiile locale P-optime, cu problemele inerente în căutarea extremelor globale sau U-set. Cu toate acestea, este posibil să găsim soluții Π prin intermediul unei căutări ordonate a punctelor X.ÎDx, de exemplu, prin noduri dintr-o rețea numerică sau printr-o metodă de căutare aleatorie.
În concluzie, observăm că în cazul în care VZLP inițială are constrângeri m1-egalitate, apoi scrie-le în jos în forma canonică pentru nu mai mult de pași OZHI m1 (poate fi dependentă liniar) VZLP redus la forma (3), (4), dar cu redus cu m1 număr de variabile libere.
1. Dubov Yu.A. Travkin SI Yakimets V.N. Modele multicriteriale pentru formarea și selectarea variantelor de sistem. - M. Nauka, 1986. - 295 p.
2. Podinovsky VV Nogin V.D. Soluții pareto-optimale ale problemelor multicriteriale. - M. Nauka, 1982. - 256 p.
3. Larichev OI Polyakov OA Proceduri om-mașină pentru luarea deciziilor cu privire la sarcinile multiple ale MP: (Revizuire). Economie și metode matematice. - 1980. - Т.16, вып. 1. - pag. 127-145.
4. Germeyer Yu.B. Introducere în teoria cercetării operaționale. - M. Nauka, 1972. - 383 p.
6. Yudin D.B. Holstein EG Probleme și metode de programare liniară. - M. Sov. radio, 1969. - 736 p.
7. Berzin E.A. Alocarea optimă a resurselor și teoria jocurilor. - M. Radio și comunicare, 1983. - 183 p.
8. Karlin S. Metode matematice în teoria jocurilor, programării și economiei. - M. Mir, 1964. - 838 p.
Trimiteți-le prietenilor: