SV Usatikov, candidat la științe fizice și matematice, conferențiar universitar; SP Grushevsky, candidat la științele fizice și matematice, profesor asociat; MM Kirichenko, candidat la Științe Sociologice
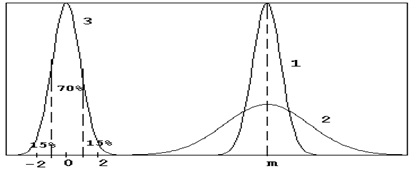
Figura 1. Densitatea probabilităților din legea normală
1,2 - grafice cu o medie m și diferite deviații standard s. unde s 1
3 - grafic pentru m = 0, s = 1 pentru legea Z și o distribuție aproximativă a suprafețelor sub curbă.
Sub argumentul X înțeles aici o varietate de valori numerice, care nu pot fi prezise înainte de experiment: înălțimea, greutatea, numărul de erori în timpul testării, dezvoltării mentale, delincvență și orice alte rezultate ca urmare a adăugarea de mai multe independente (sau slab dependente) și comparabile în ordinea influenței lor asupra influențelor aleatorii. Funcția f (x) prezintă următoarele informații importante: o valoare numerică x probabilitatea de a lua o valoare mai mare decât numărul și mai mic în număr egal cu aria de sub curba f (x) în intervalul [a, b] (Figura 1). Desigur, aceasta se aplică oricărui a și b, aproape unul de celălalt sau îndepărtat, situat oriunde în linia dreaptă x. În plus, suprafața sub întreaga curbă f (x) este 1, i. E. Probabilitatea ca x să lovească o linie este 1, iar acest eveniment este fiabil (această proprietate este numită și condiția de normalizare).
Legea normală are doi parametri care o determină complet: numerele m și s. Numărul m este valoarea medie pentru indiciile numerice care ne interesează: creșterea medie, greutatea medie, etc. Schimbarea m. se poate efectua un transfer paralel al curbei f (x) de-a lungul axei x. Se vede, de asemenea, că apariția unui număr x în experimentul apropiat de m este cel mai probabil. aria de sub f (x) pe orice interval care conține m este cea mai mare.
Numărul s reprezintă deviația medie a indexului numeric x de la numărul m: cu atât mai mic s. "mai abrupt" devine "dealul" f (x) (figura 1) și cu atât mai puțin probabilitatea pentru x este foarte diferită de m. Dimpotrivă, pentru s, e, "dealul" f (x) se întinde de-a lungul "planetei" și cu o probabilitate aproape egală x poate să apară cât mai apropiat de m. și în mod arbitrar departe de m.
Dacă valoarea numerică a lui x este recalculată la numărul Z conform următoarei reguli:
atunci toate "colinele" f (x) se vor transforma în curba 3 a legii lui Gauss din Fig. Apoi toate punctele ± 1 pentru Z corespund punctelor m ± s pentru x, iar puncte ± 3 pentru Z - pentru punctele m ± 3s pentru x. Distribuția zonei sub curba 3 arată că aproximativ 99,7% din suprafața totală sub curba f (x) este concentrată pe [-3,3]. Prin urmare, așa-numita regulă a „trei s“ pentru legea Z: cu probabilitatea p = 0,997 x valoarea aleatorie se abate de la toate „dealuri“ f (x) să devină o lege Z curba 3 din Fig.1. Apoi toate punctele ± 1 din media m (stânga sau dreapta) nu depășesc 3 secunde.
Acum este timpul să explicăm de ce se acordă atât de multă atenție "colinei" f (x) din Fig. În teoria probabilității o teoremă este dovedită, pe bună dreptate numită teorema limită centrală. În contururi grave, suma unui număr mare (aproape mai mult de 7-10) a variabilelor aleatorii independente, comparabile în funcție de influența lor asupra dispersiei sumei, respectă legea normală. De exemplu, creșterea unei persoane, care este influențată de o mulțime de factori, printre care în masă nu există nici o influență dominantă.
De la începutul secolului al XX-lea, legea lui Pearson c 2 (figura 2) sa dovedit a fi foarte utilă: în activitatea de asigurare, în constatarea cererii comerciale sau a popularității politicienilor etc.
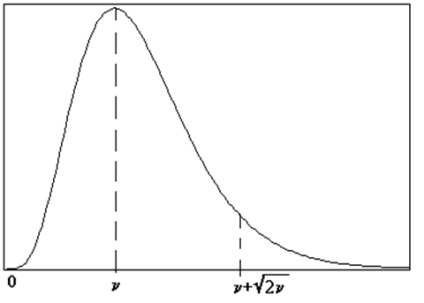
Fig.2. Densitatea distribuirii probabilității a legii este c 2, cu n grade de libertate.
Prin argumentul x se înțelege suma n termenilor independenți în pătrat, fiecare dintre ei respectând o lege Z normală cu m = 0 și s = 1. Este clar că pentru n mare (practic la n> 30) legea c 2 se transformă într-o lege normală cu m = n și s =
, deoarece teorema Lyapunov este valabilă. Dar, cel mai adesea, nu există mai mult de 10. Numărul n este numit numărul de grade de libertate. Semnificația lui f (x) este aceeași ca în legea normală: probabilitatea unei valori numerice x = c 2 care se încadrează într-un interval dat este egală cu aria de sub curba f (x). Astfel, aria de sub curba de pe segmentul de la 0 la n +
este mai mare de 90% din suprafața totală sub curba f (x). Prin urmare, ar trebui să se abțină de regulă „trei s“ pentru legea c2 cu probabilitate 0,9 PI variabilă aleatoare x = c nu depășește 2 n + 2n C (evident, c 2 nu poate fi negativă).
t legea În sfârșit, trebuie menționat Studentului obținut din legea normală și zakonac 2. aleatoare t variabilă se obține din fracțiunea în care numărătorul este Gaussian Z variabila aleatoare cu m = 0 și s = 1, iar numitorul - valoare aleatoare c 2 cu n grade libertate. Ca și înainte, pentru n mare, Legea Studentului trece în legea normală (practic la n ≥ 30). Dar chiar și pentru m nul mic, forma curbei de densitate a probabilității pentru t este foarte asemănătoare cu curba 3 din Fig. Diferența este că, în loc de s = 1 pentru Z trebuie să ia s = n / (n -2), t.e.srednee abatere de la t m = 0 este mai mare decât abaterea medie Z m = 0. În consecință, "dealul" legii t este mai blând decât "dealul" legii Z.
Toate materialele din secțiunea "Matematică"
Articole similare
Trimiteți-le prietenilor: