Să găsim determinantul matricei obținute.
# 8710; 3 = (-1) 1 + 1a11 # 8710; 11 + (-1) 2 + 1a21 # 8710; 21 + (-1) 3 + 1a31 # 8710; 31 = 16 • (3 • (-28) - (- 1) • 44) -10 • (2 • (-28) - (- 1) • (-14)) + 6 • (2 • 44-3 • (-14)) = 840
Să scriem separat variabilele X găsite
B) folosind matricea inversă.
Denumim cu A matricea coeficienților pentru necunoscuți; X este matricea coloanelor necunoscute; B este matricea-coloană a termenilor liberi, Vector B: BT = (-14,44, -28)
Cu aceste notații luate în considerare, acest sistem de ecuații are următoarea formă de matrice: A * X = B.
Dacă A - non-degenerate (determinantul său nu este zero, atunci are o matrice inversă A-1 Înmulțind ambele părți ale ecuației de A-1, obținem A-1 * A * X = A-1 * Cazare, A-1 *. A = E.
Această ecuație se numește reprezentarea matrice a soluției unui sistem de ecuații liniare. Pentru a găsi soluția sistemului de ecuații, este necesar să se calculeze matricea inversă A-1.
Sistemul va avea o soluție în cazul în care determinantul lui A este diferit de zero.
Să găsim principalul determinant.
Astfel, determinantul este de 140 ≠ 0, deci continuăm soluția. Pentru aceasta, găsim o matrice inversă în ceea ce privește complementele algebrice.
Să presupunem că avem o matrice nondegenerată A:
În cazul în care Aij - cofactor în elementul determinant aij al matricei A, care este produsul (-1) i + j pe minor (determinant), pentru N-1, obținut prin eliminarea rând I-lea și coloana J-lea în determinantul matricei A.
Matricea transpusă în matricea A are forma:
Calculăm complementele algebrice.
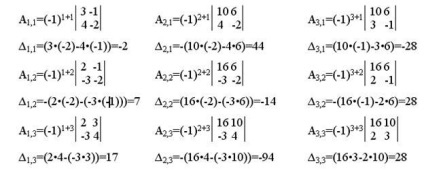
Din complementele algebrice obținute se formează matricea adjoint:
Să calculam matricea inversă:
Vectorul rezultat X X = A-1 • B
Trimiteți-le prietenilor: