- 17.04.17 09:41
- FransuaMaryDelone •
- # 288176
- Giktimes •
- 33 •
- 1800
- la fel ca Forbes, doar mai bine.
creșteri
Să începem, probabil, cu vectorii noștri preferați. Proprietatea vectorilor - pot fi desenate oriunde în spațiu, folosind un transfer paralel - această proprietate poate părea surprinzătoare. De ce? Pentru ce? Și principalul lucru este că diferite întrebări amuzante și exerciții sunt legate de acest lucru.
De exemplu: trageți un sistem de coordonate carteziene bidimensionale, un vector care începe la (0,1) și are coordonate (1,0). În grupul meu, nu toți elevii ar putea face acest lucru (datorită școlii). Al doilea curs, apropo. Ei s-au numit fizicieni mândri. Orice nonsens a fost desenat ... așa:
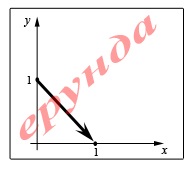
Prin urmare, o vom face o singură dată. Să tragem.
Să descriem acest algoritm "complex":
1. Marcăm punctul, care se numește "coordonatele vectorului";
2. Desenați un vector: trageți o săgeată de la "zero" într-un punct numit "coordonatele vectorului";
3. Desenați un punct numit "vectorul începe în el" - acesta va fi un "nou zero" pentru segmentul orientat (vector);
4. Transferăm vectorul nostru într-un nou început și plantă, astfel încât acesta să crească (se numește un transfer paralel).
b) Și din nou: nu vom spune cuvântul "lungimea vectorului" - acesta este un cuvânt urât. Este urât deoarece "lungimile" vectorilor au dimensiuni diferite. De exemplu, vectorul de forță are o valoare măsurată în newtoni, iar magnitudinea vectorului de deplasare este măsurată în metri. Pentru a ne aminti diferitele valori ale vectorilor diferiți, ne vom întoarce mereu înapoi. Nu spuneți niciodată cu voce tare mantra: "lungimea vectorului" - și apoi limba va cădea (gândindu-se la lungimea însăși, dar nu și pentru multă vreme). Este corect să spui: "VALOAREA unui vector" ... și respectul ușor în același timp.
c) Deci ... Când se pronunță cuvintele "coordonate vector", aceasta înseamnă că a fost pornit de la zero. Acest lucru va fi mai târziu util pentru noi, când vom semăna un câmp vectorial. Și acum acest transfer paralel va fi util pentru a vorbi despre creșteri.
Să ne uităm la imagine:
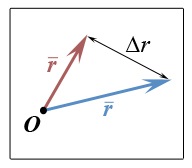
Soooo ... Un fel de vector albastru, un fel de roșu. Chemat la fel ... Și între ei se întinde o săgeată dublă ... se numește - nu este un vector - nu are început, doar două capete. În general, vorbim despre "incrementări" pe care urma să le vorbească. Prin urmare, câteva cuvinte despre ceea ce vom crește. Matematica nu-i pasă ce crește cu noi. S-ar putea da nume diferite vectorilor noștri, apoi scădea unul de la altul și se calmează. Dar vom numi ambii vectori o scrisoare și îi vom distinge prin culoare. Și vom vorbi despre creșterea "acestui vector". Imaginați-vă că acest vector se schimbă într-un fel, înseamnă ceva pentru noi. De exemplu, acest vector descrie viteza vehiculului sau forța de frecare ... Ei bine, în general, ceva ce înseamnă că, în spatele scenei, dar este - un proces de un fel, se deplasează pe cineva sau bani să-și petreacă, și poate fi încălzită - ceva se întâmplă în general, iar vectorul descrie acest lucru. În caz contrar, aceste diferite incrementări nu sunt deloc necesare și sunt lipsite de sens. În general, vreau să vă atrag atenția asupra unei subtilități, și anume, a legii de ordonare.
Dacă desenați un segment de linie (cum ar fi acest :), atunci putem suna în siguranță ce se va întâmpla (și vom obține "era delta cu o săgeată"): - incrementarea vectorului. Trebuie doar să dai seama "în ce direcție vectorul crește". Este necesar să le numerotăm cumva dacă este albastru și roșu. Cineva trebuie să-și ia libertatea și "să stabilească legea", adică spune cine este vectorul inițial și care este cel final. Ei bine, lasă-mă să o număr. Acest lucru este mai bine:
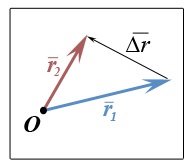
Da, mi sa părut că albastrul este vectorul inițial, iar roșul este cel final. Este ideea clară? "Avem nevoie de un motiv pentru a aranja vectorii pentru a spune care va fi prima și care al doilea." De obicei, acesta este un motiv natural, de exemplu "timpul": mai întâi a existat un vector și apoi un altul. Sau nu "timp" ... și "spațiu": coordonatele sunt mici - înseamnă începutul și coordonatele sunt mai mari - înseamnă sfârșitul. Dar unele considerații, un fel de lege de numere vectoriale este întotdeauna necesar. Da, el este întotdeauna, dar nu întotdeauna exprimat. Aici oamenii și greșit-minus, în acest loc - uitați să respecte legea, care reglementează ... Ei bine, atunci, imediat ce o astfel de lege, incrementul de ceva (cum ar fi un vector, și poate fi de orice scalar sau, Doamne iartă-mă, tensor.) Imediat automatul este calculat de o singură regulă monumentală: "END OF MINUS STARTED" - și acest lucru nu se rupe. "Începutul" este scăzut de la "sfârșit". În toate cazurile, întotdeauna, pentru totdeauna, în toți algoritmii. Acest lucru este important de reținut, pentru a nu fi greșit: mai întâi legea de ordonare, apoi "sfârșitul minus începutul". Vaughn uita-te la poza din nou: din al doilea vector scade mai întâi - primul arată la început, în creștere de la „incrementarea vectorului,“ și blocat „Incrementul“, în al doilea vector săgeată - totul aici, la sfârșitul incrementarea vectorului. Deoarece incrementul este "END OF MINUS STARTED".
Observăm că, dacă nu ar fi vorba de transferul paralel și nu de această "neglijare" pentru începutul și sfârșitul vectorului, atunci nu am fi desenat un astfel de triunghi frumos. A trebuit să trag totul de la zero. Ariciul de păr pentru arici. Aici și așa:
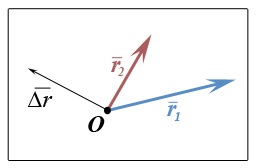
Acest lucru este, de asemenea, corect, dar mai puțin evident.
- Și unde sunt vectorii de bază. De ce nu este tras doar zero? - întrebi.
Ei bine ... vom vorbi despre sistemele de coordonate mai târziu. Și aici nu le atragem, să subliniem că nu contează - nu depinde de sistemul de coordonate adăugarea de vectori - am vrut atât de mult, am venit cu asta! Ne place că adăugarea de vectori din sistemul de coordonate nu depinde și nu există nicio justiție pentru noi! Aici suntem zei! Apropo, este prea devreme sa ne bucuram, atunci vom plati pentru aceasta divinitate, fiecare "lista noastra de pretentii" implica responsabilitate - este matematica, nu fantezie.
- Dar scuzați-mă! - vei spune. - Care este adaosul de vectori. În cazul în care. Se pare că am scos primul vector din cel de-al doilea vector. Extrase, nu sunt pliate!
Da, au făcut-o. Și noi suntem adunați, da. Aici și așa mai departe. Am fost "pliate". Doar un singur vector a fost înmulțit cu "minus unu" și nu spunea insidios nimic despre el. Ei bine, să spunem: Adăugarea și scăderea nu sunt în mod formal diferite, deoarece vectorul "" este exact același vector complet ca "" - au chiar aceeași valoare, doar arată în diferite direcții. Și toți algoritmii matematici formali pentru toți vectorii sunt la fel de buni, astfel că aceste două operații sunt numite un cuvânt "adiție" - aceasta este pentru scurtcircuit.
Sisteme de coordonate
O persoană, având în buzunar 100 denyushek, sa dus la bazar. El a privit-a privit ... într-un colț al pieței a văzut pepene verde pentru 2 denyushki pe bucată, iar într-un alt colț de pepene verde au fost mai scumpe - 3 denyushki bucată. Ura! Poți să recuperezi speculațiile! Cumpărați mai ieftin, vindeți mai mult! Pentru toți banii! Și de patru ori!
Să formăm un grafic cu privire la modul în care a făcut-o de patru ori. Observați punctele de pe planul coordonatelor acest proces de patru pași. Punctele pe care le conectăm săgeți ... Pepeni am amânat pe o verticală, și denyushki - pe orizontală. Mai mult, pentru a deveni mai amuzant, suntem huliganici: vom începe să creștem în direcția opusă, nu ca toți ceilalți (vom obține inversarea sistemului de coordonate). La început, persoana era la punctul zero: 100 denyushkas și 0 pepeni verzi, Acesta este punctul lui "zero": (100,0). Apoi a cumpărat pepeni pentru 2 denyushki pe bucată pentru toți banii! a ajuns la punctul "unu": (0.50), apoi a vândut pepeni cu profit: (150,0) și astfel de patru ori. Uite, ce frumusețe se dovedește în grafic:
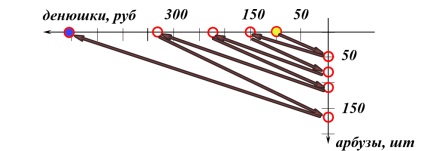
Ce credeți că există acele săgeți care se leagă de cercuri - sunt vectori?
sfârșitul celei de-a patra lecții. A continua.
Sunt de acord că, în cazul spațiului atenian, avem într-adevăr entități împărțite în vectori și puncte, pentru a nu le confunda unul cu celălalt. Acesta este într-adevăr un domeniu în care nu puteți spune doar că este același lucru. Convins.
Cu toate acestea, veți fi de acord că acest lucru este în această abstracție particulară. Când lucrați cu cantități fizice, această diviziune nu este importantă pentru dvs., deoarece un set de puncte este un spațiu liniar. În mod similar, diferențele sunt neclare în toate aplicațiile în majoritatea spațiilor. Asta este, punctul și vectorul diferă terminologic în cadrul teoriei spațiilor afine, dar ele nu diferă în aplicații.
Luați în considerare acest argument "ultimul niggard". În general, argumentul dvs. este acceptat.
Și dați un exemplu mai concret. Să luăm ca spațiu starea solidă în problema mecanicii. Avem 6 coordonate spațiale (de exemplu, centrul și 3 colțuri) și 6 viteze (permiteți viteza centrală și 3 viteze unghiulare). Soluția unei anumite probleme de control se va face în acest spațiu, de exemplu, vom instala o rachetă pe o barjă. Și acum două formulări: luăm un anumit punct al acestui spațiu, luăm un vector în spațiul dat. Spun că este absolut același lucru. Ambele sunt 12 numere reale, vectorul cu douăsprezece dimensiuni. Limbajul nu se referă la punctul de douăsprezece dimensiuni. Cu toate acestea, în aceeași problemă, există un punct pe portretul de fază. Același spațiu, aceleași 12 dimensiuni, dar cuvântul "punct".
Când avem o interpretare geometrică directă, este încă logic să facem distincția între un vector și un punct. Dar acest lucru este doar într-un număr mic de probleme geometrice, iar în cele mai multe probleme fizice chiar această interpretare dispare. Începem să multiplicăm vectori coordonatele (punctele din interpretare), să punem obiectele de-a lungul coordonatelor vectoriale și mult mai mult. De exemplu, putem multiplica coordonatele vectoriale relative ale obiectelor pentru a înțelege cine are dreptate și cine este la stânga. Când vine vorba de setul de sisteme de coordonate în mișcare, diferențele dintre vectori și puncte dispar cu totul.
Dacă luăm unghiurile (rotația), atunci vom pierde comutativitatea adăugării. Ie rezultatul întoarcerii printr-un unghi A, să zicem, în jurul axei X, și apoi la B în jurul valorii de Y, nu este același lucru ca prima întoarcere la B în jurul Y și apoi la A în jurul valorii de X.
Și ce? Cum împiedică vectorul să fie o cantitate necomutativă? Vectorul uneia dintre definiții este un set ordonat. Mai există încă o masă echivalentă. Vectorii sunt excelenți în orice spațiu, fie ea liniară, afină sau spațiul de elefanți roz. Comutativitatea este o proprietate a unui spațiu liniar, dar, în prealabil, introducem mai întâi noțiunea de vector, operații pe el, apoi comutativitate și spațiu.
Trimiteți-le prietenilor: