Proprietățile problemei de bază a programării liniare sunt legate de proprietățile seturilor convexe.
Se spune că un set de puncte este convex dacă conține, împreună cu oricare două puncte, combinația lor convexă arbitrară.
Semnificația geometrică a acestei definiții este că setul, împreună cu punctele arbitrare, aparține complet segmentului rectiliniu care îi leagă. Exemple de seturi convexe sunt un segment de linie dreaptă, o jumătate de plan, un cerc, o bilă, un cub, o jumătate de spațiu,
Punctele unghiulare ale unui set convex sunt puncte care nu sunt o combinație convexă a două puncte arbitrare ale setului. De exemplu, punctele de colț ale unui triunghi sunt vârfurile sale, cercul fiind punctele unui cerc care îl limitează.
Setul de planuri al problemei de bază a programării liniare este convex (dacă nu este gol). Un set de planuri non-goale se numește poliedrul de soluții și fiecare punct de colț al soluției polytope este un vârf.
Dacă problema de bază a programării liniare are un plan optim, atunci funcția țintă a problemei ia valoarea maximă la unul dintre vârfurile polyhedronului soluției. Dacă valoarea maximă este atinsă la mai mult de un vertex, atunci funcția țintă o ia în orice punct care este o combinație liniară convexă a acestor vârfuri.
Un set non-gol al planurilor de bază a problemei de programare liniară formează un polyhedron convex, fiecare vertex din care definește un program de suport. Pentru unul dintre planurile de sprijin (adică, într-unul dintre vârfurile deciziei polytope), valoarea funcției obiectiv este maximă (cu condiția ca funcția să fie limitată de mai sus prin setul de planuri).
Vârful deciziei polytope în care funcția obiectivului ia valoarea maximă poate fi găsit pur și simplu dacă problema din formularul standard nu conține mai mult de două variabile:
Intersecția semiplanurilor, definită de un sistem de inegalități liniare, se numește domeniul soluțiilor (OP) ale sistemului și dacă acesta satisface condițiile de non-negativitate. atunci se numește domeniul soluțiilor admise (ODR).
Dacă sistemul de inegalități este consecvent, atunci domeniul soluțiilor admisibile ale problemei este un set convex, care se numește poligonul soluțiilor. Liniile acestui poligon se află pe liniile ale căror ecuații sunt obținute din original
sisteme de restricții prin înlocuirea semnelor de inegalități cu semne de egalitate exactă.
Soluția problemei de programare liniară prin metoda geometrică include următoarele etape.
1. Linii drepte sunt construite pe plan, ale căror ecuații sunt obținute ca urmare a înlocuirii semnelor de inegalități în semne cu semne exacte.
2. Găsiți jumătățile de avion definite de fiecare dintre constrângerile problemei.
3. Creați un poligon de decizie.
4. Este construit un vector care indică direcția de creștere a funcției obiectiv.
5. Construiți funcția inițială țintă directă și apoi este deplasat paralel cu ea însăși, în direcția vectorului la punctul colț extrem al soluțiilor poligon. Ca urmare, găsirea punctul în care funcția țintă presupune valoarea maximă, sau o multitudine de puncte cu aceeași valoare maximă a funcției obiectiv alternativa optimă, în cazul în care linia de start fuzionează cu una dintre laturile de luare poligon, sau pentru a seta funcția de nemărginit de top pe un set de planuri.
6. Determinați coordonatele punctului maxim al funcției și calculați valoarea funcției obiectiv în acest punct. Valoarea minimă a funcției obiectivului liniar se găsește prin mutarea liniei inițiale în direcția opusă vectorului.
Exemplul 1. Găsiți valoarea maximă și minimă a unei funcții liniare
Soluția. Construim un poligon al soluțiilor în plan (figura 1). Pentru a face acest lucru, înlocuim inegalitățile în inegalitățile sistemului de restricții și condițiile de non-negativitate a variabilelor prin semne de egalitate exactă.
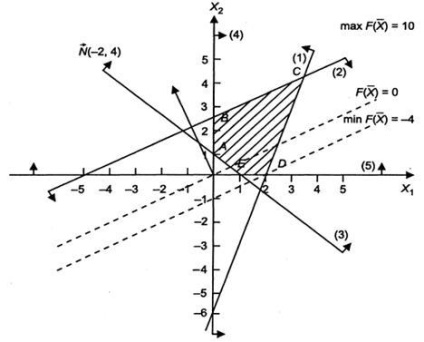
Figura 1. Construirea unui poligon de decizie
Construind sisteme directe, găsim jumătățile corespunzătoare și intersecțiile lor.
Poligonul soluțiilor problemei este pentagonul ABCDE, coordonatele punctelor ale căror puncte satisfac condiția de non-negativitate a variabilelor și inegalitățile sistemului de constrângeri ale problemei.
Pentru a găsi punctele extreme, construim linia inițială și vectorul (-2, 4). Mutarea liniei în direcția vectorului, găsim punctul C, în care linia inițială ia poziția liniei de sprijin. În consecință, la punctul C, funcția obiectiv are o valoare maximă. Deoarece punctul C este obținut ca urmare a intersecției liniilor 1
și 2 din sistem, atunci coordonatele sale satisfac ecuațiile acestor linii:
Rezolvând sistemul de ecuații obținem: = 3,4; = 4,2; de unde găsim valoarea maximă a funcției obiective = (- 2) * 3,4 + 4 * 4,2 = 10.
Prin condiția problemei, linia dreaptă inițială este paralelă cu linia dreaptă (2), deoarece coeficienții variabilelor. sunt proporționale cu: (-2) / (- 1) = 4/2 = 2. În consecință, linia inițială va ocupa poziția liniei de referință la punctele B, C și în orice punct al segmentului BC în care are aceeași valoare maximă. Pentru a determina coordonatele punctului B, rezolvăm sistemul a două ecuații liniare:
Valoarea maximă a funcției obiectiv în punctul B este:
Scriem setul de soluții optime ca o combinație liniară convexă a unghiurilor punctelor segmentului BC: unde.
Înlocuind coordonatele punctelor de colț, obținem:
Înlocuind orice valori ale lui a de la 0 la 1, obținem coordonatele setului de puncte ale segmentului BC, în fiecare dintre acestea funcția obiectivului are o valoare maximă egală cu 10.
Pentru a găsi valoarea minimă a funcției obiectiv a problemei, mutăm linia inițială în direcția opusă vectorului. Pornirea liniei presupune poziția liniei de referință la vertex D, unde k = 2, = 0, iar valoarea minimă a funcției obiectiv este: = (- 2) * 2 + 4 * 0 = -4.
Exemplul 2. Metoda geometrică pentru rezolvarea problemei de programare liniară este luată în considerare utilizând exemplul sarcinii și modelul construit al activității comerciale a întreprinderii, prezentat în clauza 2.2.1. Deoarece modelul are doar două variabile,
atunci această problemă poate fi rezolvată geometric.
Construim pe plan (figura 1) poligonul soluțiilor admisibile ale problemei. Pentru a face acest lucru, înlocuim inegalitățile în inegalitățile sistemului constrângerilor prin semnele de egalitate exactă:
Construind liniile delimitare rezultate, găsim jumătățile corespunzătoare ale valorilor admisibile ale variabilelor, apoi intersecția acestora (Figura 1).
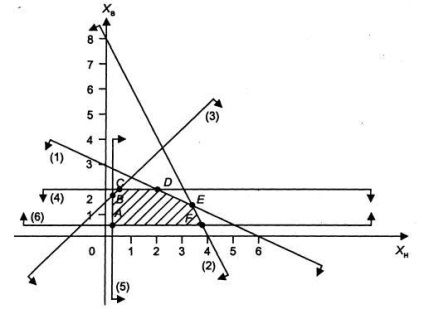
Fig.1 Construirea domeniului soluțiilor admisibile
săgețile de direcție de la fiecare linie de delimitare se determină prin substituție directă în inegalitatea unor puncte de coordonate arbitrar ales, de exemplu, (0, 0) și când satisfacerea inegalității în direcția punctului de control obiectiv săgeată altfel - dimpotrivă.
Domeniul de soluție rezultat este poligonul ABCDEF.
Punctele unghiulare ale poligonului de decizie au următoarele coordonate:
A (0,25, 0,5), B (0,25, 1,75), C (0,5,2), D (2; 2) ; 0,5).
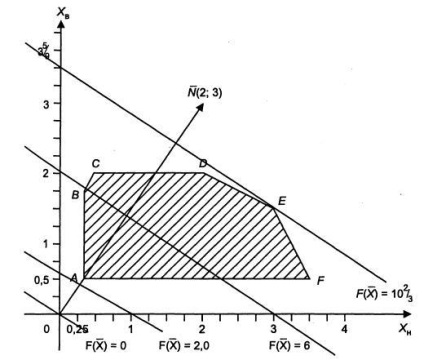
Pentru a găsi funcția obiectivului minim și maxim, construim linia inițială și vectorul de gradient (2; 3) (figura 2). Coordonatele vectorului sunt coeficienții funcției obiective liniare pentru variabilele u. Pentru a construi graficul funcției obiectiv, setați o valoare arbitrară. Dacă = 0, atunci linia trece prin origine. Pentru ao construi, setarea = 1, vom obține = -2 / 3, și la = 1, vom obține = -3 / 2 (Figura 2). Setarea 6, construim linia funcției obiectiv în același mod.
Apoi pentru = 0.25 și = 0.5, determinăm valoarea minimă = 2. Astfel, vom construi o serie de linii paralele pe grafic (Figura 2), unde vectorul de gradient (2; 3) prezintă direcția de creștere a funcției obiectiv.
Valoarea maximă va fi la punctul E. Deoarece punctul E este obținut ca rezultat al intersecției liniilor drepte (1) și (2), pentru a determina coordonatele ei rezolvăm sistemul de ecuații:
Valoarea maximă a funcției obiectiv
Funcția obiectiv traversează axa la punctul =. și axa la punctul =.
Articole similare
Trimiteți-le prietenilor: