Metoda "Sistemul Funcțiilor Iterate" (IFS) a apărut la mijlocul anilor 80 ca un simplu mod de a obține structuri fractale.
IFS este un sistem de funcții de la o anumită clasă de funcții care cartografiază un set multidimensional la altul. Cel mai simplu IFS constă în transformări plan afine:
X '= A * X + B * Y + C
Y '= D * X + E * Y + F
Transformarea afinică este o compoziție de transformare liniară și transfer paralel. Într-un spațiu bidimensional este suficient să specificăm 6 coeficienți pentru o reprezentare completă a unei transformări afine.
În 1988, cunoscuți specialiști americani în teoria sistemelor dinamice și teoria ergodică a lui Barnsley și Sloan au propus câteva idei bazate pe considerațiile teoriei sistemelor dinamice de comprimare și stocare a informațiilor grafice. Ei au numit metoda lor metoda de comprimare a informațiilor fractale. Originea numelui se datorează faptului că imaginile geometrice care apar în această metodă sunt de obicei fractale în sensul lui Mandelbrot.
Pe baza acestor idei, Barnsley și Sloan au creat un algoritm care, potrivit acestora, ar comprima informații de 500-1000 de ori. Pe scurt, metoda poate fi descrisă după cum urmează. Imaginea este codificată de mai multe transformări simple (în cazul nostru afine), adică coeficienții acestor transformări (în cazul nostru, A, B, C, D, E, F).
De exemplu, prin codarea unei imagini cu două transformări afine, definim fără echivoc aceasta folosind 12 coeficienți. Dacă specificăm acum orice punct de pornire (de exemplu, X = 0 Y = 0) și începem procesul iterativ, atunci după prima iterație obținem două puncte, după al doilea sunt patru puncte, după al treilea este de opt puncte și așa mai departe. După câteva zeci de iterații, setul de puncte obținut va descrie imaginea codificată. Dar problema este că este foarte dificil să găsim coeficienții IFS care ar codifica o imagine arbitrară.
Pentru a construi IFS, pe lângă cele afine, se aplică și alte clase de transformări geometrice simple, care sunt specificate de un număr mic de parametri. De exemplu, proiectiv:
X '= (A1 * X + B1 * Y + C1) / (D1 * X + E1 * Y + F1)
Y '= (A2 * X + B2 * Y + C2) / (D2 * X + E2 * Y + F2)
X '= A1 * X * X + B1 * X * Y + C1 * Y * Y + D1 * X + E1 * Y + F1
Y '= A2 * X * X + B2 * X * Y + C2 * Y * Y + D2 * X + E2 * Y + F2
transformări pe un avion.
Ca un exemplu de folosire a IFS pentru construirea structurilor fractale, luați în considerare curba Koch (Fig.1) și "dragonul" lui Harter-Heitway (figura 2). Se disting în aceste structuri părți similare și, pentru fiecare dintre ele, se calculează coeficienții transformării afine. Colajul afin va include cât mai multe transformări afine ca și părți ca toată imaginea.
Figura 7. Achiziții pentru construirea IFS "dragon" Harter-Heituey.
Vom construi IFS pentru "dragonul" din Harter-Heitway. Pentru a face acest lucru, aranjăm prima generație a acestui fractal pe grila de coordonate a afișajului 640 x 350 (figura 7). Semnificăm punctele din linia întreruptă rezultată A. B. C. Prin regulile de construcție, acest fractal are două părți, asemănătoare întregului - în figura 5 aceasta este ADB și BEC rupte. Cunoscând coordonatele punctelor finale ale acestor segmente, putem calcula coeficienții a două transformări afine care transferă linia întreruptă ABC la ADB și BEC.
X '= -0,5 * X -0,5 * Y + 490
Y '= 0,5 * X -0,5 * Y + 120
X '= 0,5 * X -0,5 * Y + 340
Y '= 0,5 * X + 0,5 * Y-110
Fiind dat un punct de pornire inițial (de exemplu, X = 0 Y = 0) și care acționează pe ea iterativ acest IFS, după repetare a zecea a ecranului obține structura fractale prezentată în figura 8, care reprezintă „Dragon“ Harter-Heituey. Codul său (o descriere comprimată) este setul de coeficienți ai două transformări afine.
Figura 8. "Dragonul" lui Harter-Heituey, construit cu IFS în dreptunghiul 640x350.
În mod similar, se poate construi IFS pentru curba K0. Este ușor de observat că această curbă are patru părți, asemănătoare unei curbe întregi. Pentru a găsi IFS, aranjăm din nou prima generație a acestui fractal pe grila de afișare de 640 x 350 (figura 9).
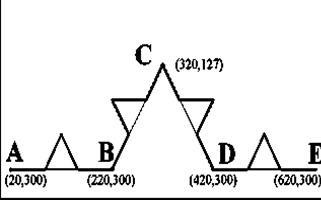
Figura 9. Piesă de lucru pentru construcția IFS Kopy Koch.
Pentru ao construi, avem nevoie de un set de transformări afine, care constă în patru transformări:
X '= 0,333 * X + 13,333
Y '= 0,333 * Y + 200
X '= 0,333 * X + 413,333
Y '= 0,333 * Y + 200
X '= 0,167 * X + 0,289 * Y + 130Y' = -0,289 * X + 0,167 * Y + 256
X '= 0,167 * X - 0,289 * Y + 403 Y' = 0,289 * X + 0,167 * Y + 71
Rezultatul aplicării acestui colaj afin după a zecea iterație poate fi văzut în figura 10.
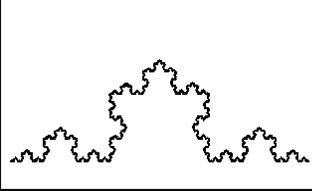
Figura 10. Koryaya Kokh, construită cu IFS în dreptunghiul 640x350.
Utilizarea de compresie IFS imagini obișnuite (cum ar fi fotografiile) se bazează pe identificarea de auto-similaritate locale, spre deosebire de fractali, în cazul în care există o auto-similaritate la nivel mondial și de a găsi IFS nu este prea dificil (suntem abia la văzut asta). Prin Barnsley algoritm este lansat în zonele de imagine ale aburului, dintre care cel mai mic este similar cu mai mulți coeficienți de conservare codificare de transformare care are o suprafață mare la o mai mică. Este necesar ca setul de zone "mai mici" să acopere întreaga imagine. În acest caz, imaginile de fișier de codificare sunt înregistrate nu numai factorii care caracterizează rezultatele de conversie, dar, de asemenea, localizarea dimensiunilor liniare ale zonelor „mari“, care, împreună cu coeficienții vor fi descrise de autosimilarității locală a imaginii codificate. Regenerating algoritm în acest caz este de a aplica fiecare transformare nu întregul set de puncte produse într-o etapă anterioară a algoritmului, și la unele subset de ele, aparținând regiunii corespunzătoare transformării aplicabile.
Unul dintre exemplele cele mai izbitoare între diferite sisteme de funcții iterate Rui este, fără îndoială, deschis M. Barnsley siste- ma patru transformări de compresiune atractor pentru care afine un set de puncte, este izbitor amintește de forma unei imagini frunze de ferigă. Acesta poate fi reprezentat sub forma tabelului următor
Fiecare linie a acestei tabele corespunde unei transformări afine cu coeficienții a, b. c, d. e, f conform expresiei
Ultima coloană a tabelului prezintă probabilitățile p. în conformitate cu care într-o metodă de iterații aleatorii se alege una sau o altă transformare.
Rezultatul acțiunii acestui sistem de funcții pe un anumit punct inițial pentru un număr diferit de iterații este prezentat în Fig. 1.43. Se poate vedea cum, pe măsură ce crește numărul iterațiilor,

Există o imagine din ce în ce mai clară a frunzei de ferigă, surprinzător, care amintește de planta existentă în natură.
Acest set de puncte este infinit de auto-similar, așa cum se presupune a fi orice fractal. Rezultă din Fig. 11, fragmentele mărite mici ale imaginii sunt similare cu întregul. Pentru a rezolva aceste fragmente, este necesar doar ca numărul de iterații să fie suficient de mare.
Astfel, cu cât este mai mare rezoluția utilizată, cu atât mai multe puncte trebuie să fie stocate în memoria computerului pentru a construi imaginea corespunzătoare. Pe de altă parte, amintirea coordonatelor acestor puncte nu este deloc necesară, deoarece acestea pot fi preluate de fiecare dată utilizând sistemul de funcții specificat de tabel

Fig. 11. Fragment crescut de frunză de ferigă
Prin urmare, doar 28 de numere conțin toate informațiile necesare despre această cifră netrivială! Există o idee și dacă este imposibil în mod similar să "cod" și alte imagini. Această idee, realizată în practică, ar permite comprimarea imaginilor în zeci sau chiar sute de ori. De fapt, în 1988, a fost implementat cu succes de Barnsley și Sloan în compania comună pe care au creat-o pentru a codifica și comprima informații grafice utilizând un sistem de funcții selectat corespunzător.
Pentru a genera modele fractale, puteți scrie un algoritm de program în Pascal, BASIC sau în alte limbi de programare. Există o mulțime de literatură în care algoritmul programului de generare a fractalilor este discutat în detaliu, de exemplu, RM Kronover "Fractalii și haosul în sisteme dinamice. Fundamentele teoriei ", conținutul teoriei fractalilor, precum și exemplele de scriere a programelor de generare a fractalilor. Dar până în prezent, există un număr mare de programe deja scrise pentru generarea desenelor fractale. Luați în considerare unul dintre ele, Fractal Explorer versiunea 2.02.
Când porniți Fractal Explorer, apare o fereastră goală, bara de instrumente este deasupra.
În stânga sunt șase pictograme. Primele cinci pentru a genera altele noi, și a șasea pentru a deschide anterior salvat. De exemplu, când faceți clic pe prima pictogramă, Mandelbrot Fractal începe să fie generat, iar generația are loc în timp real. În meniul Dimensiune, puteți schimba rezoluția pentru o imagine fractală. În mod implicit 300 x 300, din lista permisiunilor acordate puteți fie să adăugați sau să scăpați. Atunci când rezoluția este mărită, fractalul este generat mai mult decât înainte, deoarece devine mai dificil calculatorul să calculeze fractalul pentru mai multe puncte. Cu un dublu clic pe butonul stâng al mouse-ului, fractal crește, dar nu pur și simplu devine mai mare, dar calculat din nou. După generarea fractalului, puteți schimba câțiva parametri ai generației fractale. Când apăsați, apare o fereastră,
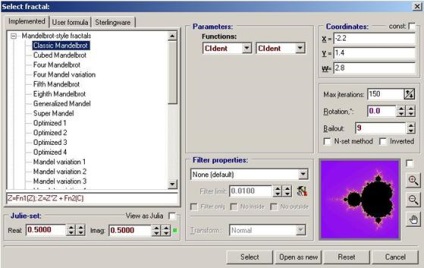
în care puteți modifica formula iterativă, numărul de iterații, parametrii funcției și multe alte setări.
Este, de asemenea, posibil să se construiască un sistem de funcții iterate, a cărui fractal este o frunză de ferigă. Implicit, această repetare este de 100 iterații. Și dacă frunza de frunze începe să crească, atunci la o creștere relativ mică este clar că ea constă din puncte. La schimbarea a 100 de iterații la 5000, partea mărită a frunzei de ferigi constă deja dintr-o mulțime de broșuri de fern.
La sfârșitul descrierii programului Fractal Explorer, putem spune că este foarte interesant să observăm atunci cum este desenat fractalul, care paletă este pictată. Foarte ca un fractal, puteți salva sau imprima.
Poate că în viitor noi idei de geometrie fractală ne vor ajuta să studiem multe fenomene enigmatice ale naturii înconjurătoare.
În prezent, fractalii și multifractalii invadează rapid multe domenii ale fizicii. Procesele de prelucrare a imaginilor fractale și tehnicile de recunoaștere a modelelor, folosind noi concepte, permit cercetătorilor să aplice acest aparat matematic pentru descrierea cantitativă a unui număr imens de obiecte și structuri naturale.
Articole similare
Trimiteți-le prietenilor: