Magazinul fabricii de cofetărie produce trei grupe de bomboane de sortimente, denumite condiționat M1. M2. M3 / în unități.
Pentru producția lor, se folosesc principalele tipuri de resurse / materii prime / de trei tipuri, denumite în mod condiționat P1. P2. P3 / în unități.
Cheltuielile fiecărei resurse pentru producerea unei unități de producție reprezintă o valoare dată, este determinată de rețetă și este marcată de simbolurile a11. A12. A33. unde a este rata de consum, primul indice 1 este numărul de resurse, al doilea este indicele 1, 2, 3 este numărul sortimentului de dulciuri.
Disponibilitatea fiecărei resurse pentru producerea tuturor grupurilor de bomboane este acceptată ca o cantitate cunoscută și este marcată de simbolurile b1. B2. B3.
Profitul pe producție este, de asemenea, acceptat ca o cantitate cunoscută și este notat cu simbolurile c1. c2. c3.
Parametrii enumerați sunt cantități cunoscute și sunt exprimate în unități unificate, cu excepția profitului. Indicatorul de profit sau alt indicator, care este criteriul optimalității, este exprimat în unități de măsură a venitului (de exemplu, profit) obținută din producția unei unități de producție în formă monetară sau într-o altă formă.
Deoarece soluția problemei constă în găsirea unui plan de producție care să asigure cele mai mari venituri în condițiile adoptate, cantitățile necunoscute și care denotă cantitățile fiecărui grup de dulciuri incluse în planul de producție sunt luate: x1 pentru M1; x2 pentru M2; x3 pentru M3.
Model economico-matematic într-o formă simbolică.
Condițiile pentru nonnegativitatea necunoscutului x1 ≥ 0, x2 ≥ 0, x3 ≥ 0
Modelul simbolic umplut cu informații numerice va avea următoarea formă:
Profitul din vânzările produselor trebuie să fie maxim, adică F = 20х1 + 24х2 + 28х3 = max;
Pentru a rezolva problema printr-o metodă simplă, inegalitățile sunt transformate în ecuații echivalente, adăugând la fiecare inegalitate un necunoscut suplimentar cu coeficientul + 1 și o ecuație zero pentru -s. Pentru confortul calculelor, părțile stângi și drepte ale ecuațiilor schimbă locurile. În acest caz, inegalitățile inițiale iau forma ecuațiilor simplex:
Coeficienții pentru necunoscute sunt înregistrați în tabelul simplex, în care sunt efectuate calculele și rezultatele sunt reflectate.
Apoi elementele din coloana X0 (valori libere) sunt împărțite la coeficienții corespunzători ai coloanei cheie și rezultatele sunt comparate una cu cealaltă. Șirul cu cel mai mic raport este considerat cheie și este de asemenea evidențiat pentru confort. În cazul nostru, 266/3 = 88,7; 200/4 = 50; 303/1 = 303. Cel mai mic raport de 50 este al termenului x5. acesta va fi cheia. Elementul cheie 4.
Elementele tabelului sunt apoi convertite și scrise într-un tabel nou. Inițial, elementele șirului cheie sunt convertite prin împărțirea lor într-un element-cheie. Elementele convertite sunt scrise în același loc.
În coloanele Po și Cj, necunoscutul x3 introdus în plan ocupă locul cu 28 (iterația I). Restul elementelor sunt convertite conform următoarei reguli:
- pentru elementul care trebuie transformat, elementul șirului-cheie este găsit în coloana sa, iar în rândul său este elementul coloanei cheie;
- elementele corespunzătoare ale rândului de chei și ale coloanei de tastă se înmulțesc, iar produsul rezultat este împărțit într-un moment cheie;
- coeficientul din diviziune este scăzut din valoarea elementului pe care la avut înainte transformării și rezultatul este un element transformat care este scris într-un tabel nou în același loc. Urmând această regulă, transformarea elementelor din coloana x0 va fi:
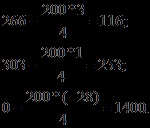
Includerea la prima iterație în planul necunoscutului x3 va oferi suma de profit de 1400 de ruble.
Soluția problemei continuă, deoarece există două elemente negative în linia țintă. Cel mai mare element este -13. Este în coloana x1. care este luată ca cheie, iar linia cheie va fi x6 (116: 1,3 = 92,8, 50: 0,3 = 200; 253: 2,8 = 92); elementul cheie este 2,8. Elementele mesei se transformă în aceeași ordine conform regulii de mai sus și se scriu într-un tabel nou.
În ultimul tabel, rândul țintă are numai elemente pozitive. Aceasta înseamnă că planul este optim și că îmbunătățirea ulterioară este imposibilă.
După cum se poate observa din tabel, planul optim prevede producția de unități P1 27. (x1 = 27), P3 92 de unități. (x3 = 92), o necunoscută suplimentară n. (x4 = 1). N2 și alte necunoscute nu au intrat în plan, deci x2 = 0, x5 = 0 x6 = 0. Înlocuindu-ne necunoscute în ecuații, obținem:
2 * 92 + 4 * 0 + 3 * 27 + 1 = 266
1 * 92 + 3 * 0 + 4 * 27 + 0 = 200
3 * 92 + 2 * 0 + 1 * 27 + 0 = 303
F = 20 * 92 + 24 * 0 + 27 * 28 = 2596
Analiza planului optim.
a) Stocurile de materii prime de trei tipuri nu sunt pe deplin utilizate, deoarece x4 = 1 și x5 = x6 = 0.
b) Luați în considerare elementele matricei.
De la eliberarea producției II ar trebui abandonată.
Elementele din coloana x5 arată că creșterea rezervelor de zahăr de către unitatea I. (х5 = 1) va permite creșterea volumului de producție de tip III pe 0,3 unități. Valoarea profitului va crește cu 5,8 ruble.
Elementele din coloana x6 arată că o creștere a rezervelor de grăsime cu 1 unitate. (x6 = 1) va reduce producția numai a produselor de tip III cu 0,1 unități. (27 - 0,1) Suma la-a crescut cu 4,7 ruble.
Reducerea stocurilor de materii prime conduce la modificări ale producției și la valoarea profitului în ordine inversă.
Elementele liniei țintă a planului optim sunt numite estimări duale, care determină valoarea modificării profitului atunci când rezervele de materii prime se modifică cu 1 unitate.
Este necesar să se determine amestecul minim de costuri de materii prime pentru prepararea concentratelor alimentare, care trebuie să conțină substanțe nutritive (P). Aceste substanțe sunt conținute în materiile prime (M) în diferite combinații. Conținutul de nutrienți din materiile prime și produsele finite, precum și prețul fiecărui tip de materii prime sunt prezentate în tabel.
Elementele liniei țintă sunt calculate conform regulilor uzuale și se obțin semne negative.
Spre deosebire de procedura computațională a metodei simplex de bază, soluția problemelor prin metoda dublă se realizează în ordine inversă.
În coloana finală, numerele libere au semne negative. Aceasta este o dovadă a faptului că acest plan nu poate fi considerat admisibil, deoarece contravine sensului economic. Planul poate fi considerat valabil numai dacă nu există numere negative în coloana finală.
Eliminarea numerelor negative din coloana finală începe cu valoarea cea mai mare în valoare absolută. În exemplul nostru, acest număr este (-140). String x5. în care este situat acest număr, este considerat drept cheie și este evidențiat în mod corespunzător.
După ce am determinat șirul cheie, găsim coloana cheie. Pentru a face acest lucru, trebuie să împărțiți elementele liniei țintă în elemente ale șirului de chei și să alegeți cele mai mici din relațiile obținute. O coloană care are cel mai mic raport este presupusă a fi o coloană cheie și, la fel ca un șir cheie, este alocată.
Coloanele x1. x2. x3 va avea următoarele relații:
Cea mai mică rată este coloana x1 și va fi cea mai importantă.
După determinarea șirului cheie, a coloanei cheie și a numărului de cheie, în conformitate cu regulile obișnuite, toate elementele matricei sunt transformate și scrise în noul tabel.
Soluția problemei începe cu distribuirea volumelor de export între consumatori care sunt disponibile de la furnizori, luând în considerare volumele de livrare. Pentru distribuția inițială se utilizează metode: colțul nord-vestic, cel mai mic element din rând, cel mai mic element din coloană, cel mai mic element al matricei.
Calea colțului nord-vestic este că distribuția volumelor de export se face începând cu colțul din stânga sus al mesei și se termină cu colțul inferior al mesei. Rezultatele distribuției sunt prezentate în tabel.
Furnizori și volume de export, t
Consumatori și volume de livrare
Verificarea planului de optimitate. Când se primește planul inițial și se calculează cantitatea totală de tone-kilometru corespunzătoare, se determină dacă acest plan este optim. Pentru a verifica planul de optimitate, se aplică metoda potențialelor.
Esența metodei potențiale este aceea că pentru fiecare rând și fiecare coloană a tabelului (matricea) sunt definite numere speciale, numite potențiale. Cu ajutorul acestor potențiali este posibil să se determine dacă este necesar să se umple o celulă liberă a matricei sau trebuie lăsată nefolosită.
Pentru a rezolva probleme folosind metoda potențială, planul inițial trebuie să aibă numărul de celule umplut m + n - 1 (m este numărul de rânduri, n este numărul de coloane). Dacă planul nu îndeplinește aceste cerințe, atunci nu toate rândurile și coloanele pot fi calculate potențiale și fără ele nu puteți verifica planul pentru optimalitate.
Potențialele rândurilor și coloanelor sunt determinate de celulele umplute la intersecția lor.
Elementul celulei umplute trebuie să fie egal cu suma potențialelor rândului și coloanei la intersecția căreia este localizată această celulă umplută.
Pentru a începe calculele, se presupune că primul potențial pentru un rând sau o coloană este condițional zero, toate celelalte potențiale sunt determinate de elementele celulelor umplute.
Denotând potențialul rândurilor ui. potențialele coloanei Vj, elementele de umplere a celulelor
, putem scrie ordinea de calcul a potențialelor pentru cazul general.
Din cerința de bază
= ui + Vj urmează:
Din aceste expresii se vede că pentru a calcula potențialul unui șir este necesar să existe o celulă umplută în coloana a cărei potențial este deja definită și să se calculeze potențialul coloanei, este necesară o celulă umplută având un potențial într-un rând.
Potențialele sunt prezentate în tabel.
După ce potențialul este determinat de rânduri și coloane, acesta este utilizat pentru a determina dacă planul este optim și dacă nu, cum poate fi îmbunătățit. În acest scop, pentru fiecare celulă liberă, se calculează suma potențialelor rândurilor și coloanelor, la intersecția dintre care se află această celulă.
Compararea sumei potențialelor cu valoarea elementului în celulele libere ne permite să determinăm dacă este necesar să umplem această celulă sau să o lăsăm liberă.
Atunci când rezolvăm probleme pentru un minim de funcțional (în cazul nostru, la o operare de cel puțin o tonă-kilometru), acele celule libere nu sunt completate în care suma potențialelor este mai mică decât valoarea elementului (în cazul nostru, distanțele).
Cu alte cuvinte, dacă caracteristica a cărei valoare este egală cu diferența
- (ui + Vj), pozitiv, atunci marcajul liber nu este umplut la rezolvarea problemei funcției minime.
Celulele libere care au o valoare caracteristică zero arată că umplerea acestora va duce la o redistribuire a consumabilelor, dar cantitatea de muncă (valoarea funcțională) va rămâne neschimbată.
Sumele potențialelor, valorile elementelor și caracteristicile celulelor neincluse sunt date în tabel.
În planul inițial, șase celule au caracteristici pozitive, în nouă celule caracteristicile sunt negative.
Deoarece problema este rezolvată pentru un minim de funcție obiectivă, aceste celule negative trebuie să fie completate de furnizori. Dar umplerea celulei libere și re-distribuția asociată a consumabilelor nu se fac în mod izolat, ci în legătură cu mai multe celule umplute. Această relație este revelată prin construirea de poligoane închise, ale căror vârfuri sunt celulele tabelului. Un vârf al poligonului este în celula liberă, iar toate celelalte sunt în celulele pline. Un poligon, sau așa cum se numește lanț, are unghiuri drepte și un număr par de vârfuri.
Ca urmare a redistribuirii în fiecare vertex (cușcă) lanțului, cantitatea de livrări se modifică: în unele celule acestea cresc, în altele se diminuează.
Acele celule ale lanțului ale căror creșteri ale livrărilor sunt numite pozitive, iar cele ale căror livrări scad negative. Fiecare lanț are același număr de vârfuri pozitive și negative (celule). Vitezele pozitive și negative alternează. Dacă celula liberă în care se presupune că este înregistrată este considerată pozitivă (deoarece schimbarea va crește), atunci celula următoare va fi negativă, apoi din nou pozitivă, din nou negativă etc.
Din celulele libere care trebuie umplute, se alege o celulă care are de obicei cea mai mare caracteristică negativă. Înregistrează cea mai mică valoare a vârfurilor negative ale lanțului.
+P4M1-P1M1 + P1M2-P2M2 + P2M4-P3M4 + P3M5-P4M5
Furnizori și volume de export, t
Consumatori și volume de livrare
+P2M5-P4M5 + P4M1-P1M1 + P1M4-P2M4
Furnizori și volume de export, t
Consumatori și volume de livrare
+P2M5-P4M5 + P4M1-P1M1 + P1M4-P2M4
Furnizori și volume de export, t
Consumatori și volume de livrare
+P3M2-P1M2 + P1M4-P2M4 + P2M5-P3M5
Furnizori și volume de export, t
Consumatori și volume de livrare
+P4M3-P2M3 + P2M5-P4M5
Furnizori și volume de export, t
Consumatori și volume de livrare
+P2M1-P2M3 + P4M3-P4M1
Furnizori și volume de export, t
Consumatori și volume de livrare
+P2M2-P2M5 + P3M5-P3M2
Furnizori și volume de export, t
Consumatori și volume de livrare
Toate celulele libere au caracteristici pozitive, ceea ce indică faptul că îmbunătățirea ulterioară a planului este imposibilă, iar planul rezultat este optim.
Domeniul de activitate va fi: 32 * 30 + 112 * 15 + 76 * 9 + 52 * 24 + 20 * 27 + 76 * 21 + 16 * 11 + 80 * 27 + 36 * 8 = 9332 tkm.
Toate materialele din secțiunea "Modelarea economică și matematică"
Articole similare
Trimiteți-le prietenilor: