1.6 Echivalența triunghiurilor. Teorema lui Bolja-Gervin
Multe formule și teoreme în geometrie se dovedesc prin tăierea unor forme și apoi prin rearanjarea părților lor - să ne reamintim, de exemplu, teorema lui Pitagora. Dacă cele două figuri pot fi tăiate la același set de părți (de ex., E. Între părțile acestor seturi pot fi setate la o singură corespondență, în care părțile respective sunt egale), aceste cifre sunt numite equidecomposable. Cifrele echidistant, desigur, sunt egale în mărime - au zone egale. Pentru poligoane, teorema inversă este de asemenea adevărată: oricare doi poligoane egale cu dimensiuni sunt echiducabile. În 1832, a fost dovedit de matematicianul maghiar Farkash Bolyai, iar un an mai târziu, dar independent de el, germanul P. Gervin. Cheia dovada - redesenarea dreptunghiului prezentat în Figura 1.40: tăiere dreptunghi „scăzut“ în două triunghiuri și un pentagon, triunghiuri de alunecare de-a lungul liniei de secțiune înclinată, vom obține un alt, dreptunghi „mare“.
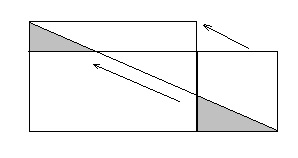
În acest fel, acest dreptunghi nu este greu să se transforme în aproape orice altul egal cu el - este necesar doar ca noul dreptunghi să fie "mai mare" decât originalul, dar nu mai mult de două ori. Dacă raportul dintre înălțimile dreptunghiuri mai mari de două (Fig. 1.41, a) „low“ pentru a „face mai mare“, printr-o simpla transformare (Fig. 1.41, b) aplicat în mod repetat.
Acum, orice poligon poate fi remodelat într-un dreptunghi de înălțime fixă h. l-am tăiat în triunghiuri, transformăm fiecare triunghi într-un dreptunghi (vezi Figura 1.42), reducem dreptunghiurile rezultate la o înălțime constantă h și le aliniem vertical.
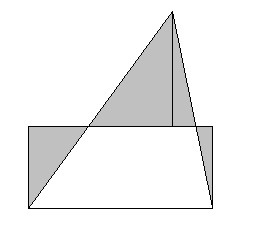
Dacă două triunghiuri au dimensiuni egale, atunci dreptunghiurile corespunzătoare la o anumită înălțime constantă h sunt egale. Astfel, aceste poligoane sunt echivalente cu aceeași figură, și de aici deducem deja că ele sunt echivalente.
1.7 Raportul ariilor de triunghiuri similare
Teorema 1. Zonele a două triunghiuri având un unghi egal sunt tratate ca produse ale laturilor care acoperă aceste unghiuri.
Dovada. Să presupunem că unghiurile A și A sunt egale în triunghiurile ABC și (Figura 1.43).
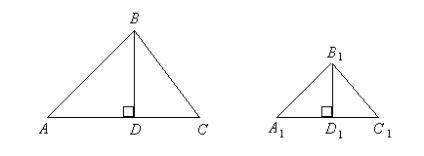
După ce am purtat înălțimile și vom avea:
Triunghiurile sunt similare (A = A1 și D = D1 = 90 0); înlocuind primul raport cu cel de-al doilea, obținem:
Teorema 2. Zonele de poligoane similare sunt denumite pătrate de laturi similare.
Dovada. 1) Dacă u sunt două astfel de triunghiuri, atunci unghiurile unuia sunt egale cu unghiurile celuilalt; lasa
Aplicăm teorema precedentă acestora:
Dar din similitudinea triunghiurilor rezultă:
Prin urmare, în ecuația (1.14) putem înlocui fiecare dintre relații prin orice relație din serie (1.15), prin urmare,
2) Dacă u (Figura 1.44) are doi poligoane similare, atunci ele pot fi descompuse într-un număr egal de triunghiuri asemănătoare și dispuse identic.
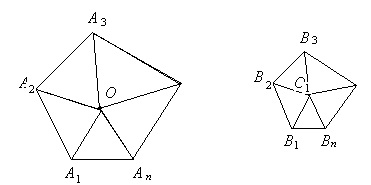
Lăsați aceste triunghiuri să fie:
Conform a ceea ce sa dovedit în prima parte a acestei teoreme, obținem proporțiile:
Dar din similitudinea poligoanelor urmează:
Corolar. Zonele de poligoane regulate de același nume sunt denumite pătrate ale laturilor sau ca pătrate de raze de apograme.
1.8 Cifrele cu cea mai mare suprafață
1.8.1 Trapezoid sau dreptunghi
Începem să analizăm acest punct rezolvând problema.
Sarcina. În ziua fatidică a vieții sale, Pachom a trecut de 40 de mile, mergând de-a lungul laturilor trapezoidului cu o suprafață de 78 de kilometri pătrați. Intenția lui inițială era să se plimbe de-a lungul laturilor dreptunghiului, trapezul sa dovedit din întâmplare, ca urmare a calculului slab. Este interesant să se stabilească dacă a ghicit sau a pierdut din faptul că intriga lui nu era un dreptunghi, ci un trapez. În ce caz ar fi primit o suprafață mare de teren?
Soluția. Dreptunghiurile cu o circumferință de 40 de versturi pot fi foarte multe și fiecare are o zonă diferită.
Iată câteva exemple:
14 6 = 84 de metri pătrați. guri de aerisire
13 7 = 91 de metri pătrați. guri de aerisire
12 8 = 96 de metri pătrați. guri de aerisire
11 9 = 99 de metri pătrați. guri de aerisire
Vedem că pentru toate aceste figuri, în același perimetru, 40 verstale sunt mai mari decât trapezul nostru. Cu toate acestea, sunt posibile astfel de dreptunghiuri cu un perimetru de 40 de verșuri, a căror suprafață este mai mică decât cea a trapezoidului:
18 2 = 36 de metri pătrați. guri de aerisire
19 1 = 19 metri pătrați. guri de aerisire
19,5 0,5 = 9,75 metri pătrați. guri de aerisire.
În consecință, nu se poate da un răspuns clar la problema problemei. Există dreptunghiuri cu o suprafață mai mare decât trapezul, dar sunt mai mici, cu același contur. Dar puteți da un răspuns foarte clar la întrebarea: care dintre toate figurile dreptunghiulare cu perimetrul dat cuprinde cea mai mare zonă? Comparând dreptunghiurile noastre, observăm că cu cât diferența dintre lungimea laturilor este mai mică, zona dreptunghiului este mai mare. Este normal să se concluzioneze că atunci când această diferență nu este deloc, adică atunci când dreptunghiul devine un pătrat, aria cifrei va ajunge la cea mai mare valoare. Va fi egal cu 10 10 = 100 de metri pătrați. guri de aerisire. Este ușor de văzut că acest pătrat depășește cu adevărat în zonă orice dreptunghi al aceluiași perimetru cu el. Pahom ar fi trebuit să meargă de-a lungul părților laterale ale pieței pentru a obține locul celei mai mari zone - 22 de pătraturi mai mult decât ar fi putut acoperi.
1.8.2 Proprietatea remarcabilă a pieței
O proprietate remarcabilă a unui pătrat este de a închide în limitele sale cea mai mare zonă în comparație cu toate celelalte dreptunghiuri ale aceluiași perimetru. Dăm o dovadă riguroasă.
Denumim perimetrul unei figuri dreptunghiulare cu P. Dacă luăm un pătrat cu un astfel de perimetru, fiecare parte a acestuia trebuie să fie egală. Să demonstrăm că prin scurtarea unei laturi la o anumită valoare a lui b cu aceeași alungire a laturii adiacente obținem un dreptunghi cu același perimetru, dar mai mic decât suprafața. Cu alte cuvinte, dovedim că aria pătratului este mai mare decât aria dreptunghiului:
Din moment ce partea dreaptă a acestei inegalități este egală, întreaga expresie ia forma: sau.
Dar ultima inegalitate este evidentă: pătratul oricărui număr, pozitiv sau negativ, este mai mare decât zero. În consecință, egalitatea originală care ne-a condus la acest lucru este, de asemenea, adevărată.
Deci, pătratul are cea mai mare suprafață a tuturor dreptunghiurilor cu același perimetru.
De aici rezultă că din toate figurile dreptunghiulare cu aceleași suprafețe, pătratul are cel mai mic perimetru. Acest lucru se poate vedea din argumentul următor. Să presupunem că acest lucru nu este adevărat și că există un dreptunghi A care, pentru o zonă egală cu pătratul lui B, are un perimetru mai mic decât cel al lui. Apoi, prin tragere la pătrat Cu același perimetru ca și cel al dreptunghi A. obține un pătrat având o suprafață mai mare decât în A. și, prin urmare, mai mare decât cea a unei V. pătrat Ca rezultat, au descoperit că un pătrat C are un perimetru mai mic decât pătrat B. și zona este mai mare decât el. Acest lucru este evident imposibil: odată ce partea laterală a pătratului C este mai mică decât partea pătratului B. atunci zona ar trebui să fie mai mică. Prin urmare, era imposibil să recunoaștem existența unui dreptunghi A. care, cu aceeași zonă, are un perimetru mai mic decât cel al pieței. Cu alte cuvinte, din toate dreptunghiurile cu aceeași zonă, cel mai mic perimetru are un pătrat.
Familiarizarea cu aceste proprietăți ale pătratului la ajutat pe Pakhom să își calculeze corect forțele și să obțină o secțiune dreptunghiulară din cea mai mare zonă. Știind că el poate trece o zi fără stres, de exemplu, 36 de guri de aerisire, el va merge de-a lungul graniței unui pătrat cu latura de 9 de mile, iar seara va fi proprietarul site-ului în 81 mile pătrate - 3 mile pătrate mai mult decât a primit fatal tensiunea forțelor. Pe de altă parte, în cazul în care a fost limitat în prealabil cu privire la orice domeniu specific zonei dreptunghiulare, de exemplu, 36 de verste pătrate, s-ar putea obține un rezultat cu cel puțin cheltuielile de energie, trecând peste limita unui pătrat a cărui latură - 6 guri de aerisire.
Articole similare
-
Rezumat ce este pădurea băncii de rezumate, eseuri, rapoarte, lucrări de curs și diplome
-
Pedeapsa cu moartea ca formă de pedeapsă este o lucrare de termen, pagina 1
Trimiteți-le prietenilor: