Diferențe finite ale diferitelor comenzi
y = f (x) este notat cu
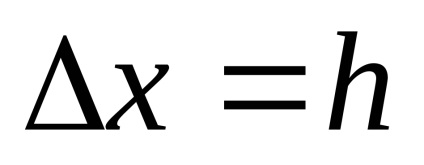
Să găsim incrementarea funcției
Se numește diferența finală 1, diferența finală n este calculată prin formula:
Fie f (x) un polinom de grad n
Proprietățile diferențelor finite:
Exprimăm diferențele finite în ceea ce privește funcțiile
Să presupunem că funcția y = f (x) are derivatul nth pe interval, atunci putem scrie că derivatul nth al funcției
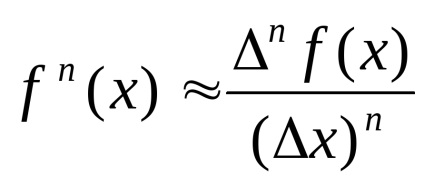
Tabel diferență finită
Trebuie să luăm în considerare funcția dată în tabel
Diferențele finite ale secvenței yi sunt definite de relație
Ne amintim binomul lui Newton, se poate arăta că a șaptea diferență finală yi poate fi reprezentată ca sumă
Aceste diferențe finite sunt aranjate convenabil sub formă de tabele:
De cele mai multe ori, în practică, se folosește o masă orizontală, arată astfel:
Declarația problemelor de aproximare a unei funcții, o problemă generală de interpolare, cea mai simplă problemă de interpolare.
O putere generalizată n a unui număr x este produsul factorilor n din care primul este x, iar fiecare este factorul următor. pe h este mai mică decât cea anterioară.
X [n] este denumirea.
Să găsim diferența finită pentru puterea generalizată.
Declarația problemei interpolării
Cele mai simple probleme de interpolare sunt următoarele:
Aceste puncte sunt numite noduri de interpolare, pentru aceste noduri de interpolare, valoarea unor funcții y = f (x)
Funcția F (x) se numește interpolare.
Expresia analitică f (x) este foarte complexă sau necunoscută.
Geometric, acest lucru înseamnă că este necesar să se găsească y = F (x), cu unele proprietăți suplimentare, în special F (x), trece prin punctul (xi, yi), yi = f (xi) i = 1, n
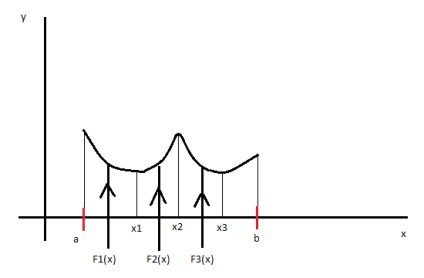
Problema din această formulă poate avea un set infinit de soluții.
Problema devine rezolvată în mod unic, în cazul în care funcția y = f (x) polinomul considerat y = Pn (x) de grad nu mai mare de n, care satisface condiția Pn (xi) = yi i = 0, n.
n- număr de puncte. Funcția de interpolare rezultată este adesea folosită pentru a aproxima valorile funcției y = f (x) în punctele care nu coincid cu nodurile de interpolare
O astfel de operație se numește interpolarea funcției f (x).
Interpolarea se distinge într-un sens îngust și într-un sens larg. Această operație se numește extrapolare.
Prima formulă de interpolare a lui Newton (formula generală și formulele pentru interpolarea liniară și patratică).
Fie y = f (x) dată de punctele sale yi = f (xi) i = 0, n, unde xi = x0 + ih. h este etapa de interpolare.
Considerăm un polinom de grad y = Pn (x) care satisface condiția Pn (xi) = yi (1)
Condiția (1) este echivalentă cu egalitatea:
Calculând prima diferență finită a polinomului Pn (x) (vezi (2)) și presupunând că x = x0, obținem
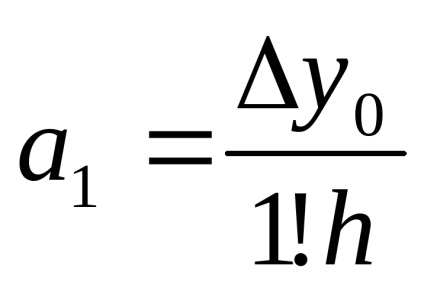
Găsirea celei de-a doua diferențe finite și cea înclinată care x = x0
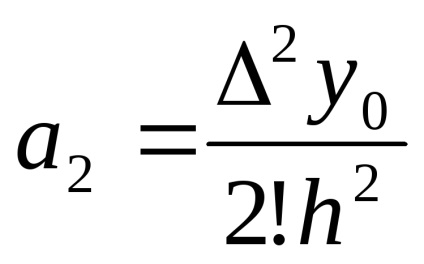
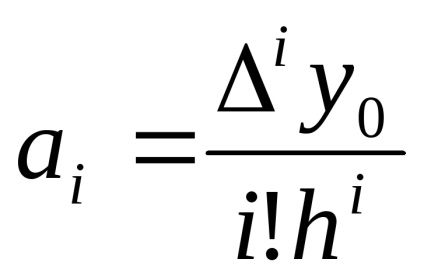
Înlocuirea coeficientului ai în (3). obținem:
- primul polinom Newton.
De obicei, primul polinom Newton este scris într-o formă mai convenabilă:
Formula (4) este incomodă pentru aplicarea practică. Prin urmare, a fost introdus al doilea polinom Newton de interpolare:
Trimiteți-le prietenilor: